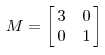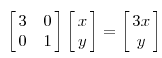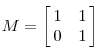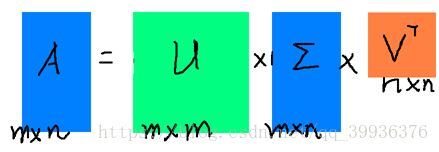A Singularly Valuable Decomposition(SVD奇异值分解)

A Singularly Valuable Decomposition(SVD奇异值分解)

        SVD与熟悉的对称矩阵对角化理论密切相关。 如果A是对称实数n×n矩阵，则存在正交矩阵V和对角线D，使得A= 。 这里V的列是A的特征向量，并形成Rn的正交基; D的对角线上的数值是A的特征值。为了强调与SVD的联系，我们将称为A的特征值分解或EVD。

        对于SVD，任意一个实数m×n矩阵A，存在正交矩阵U和V以及一个对角矩阵，这次表示为Σ，使得A = 。 在这种情况下，U是m×m矩阵，V是n×n矩阵，所以Σ是与A的尺寸相同的矩形。Σ的对角线上的数值，即Σii=σi，可以排列成非负的并且是按幅度减小的顺序排列的。正数值σi称为A的奇异值，U和V的列称为A的左和右奇异向量。        

        下面先介绍一下特征值（EVD）分解：

        如果说一个向量v是方阵A的特征向量，将一定可以表示成，这时候被称为特征向量v对应的特征值。

        一个矩阵的一组特征向量是一组正交向量。特征分解是将一个矩阵分解成A = ，其中V是这个矩阵A的特征向量组成的矩阵，D是一个对角矩阵，每个对角矩阵上的元素就是一个特征值。

        一个矩阵变换可以看成为一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。举例如下：

 eg1. 矩阵M如下：

它对应的线性变换如下面形式：

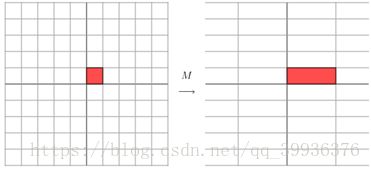
用图形描述为：

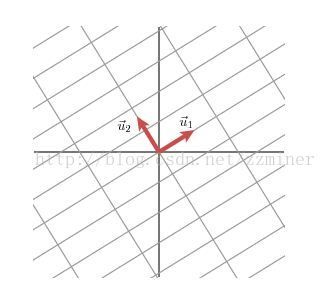
        上面的矩阵是对称的，所以这个变换是一个对x，y轴的方向一个拉伸变换（每一个对角线上的元素将会对一个维度进行拉伸变换，当值>1时拉长，当值<1时缩短），当矩阵不是对称的时候，假如说矩阵是下面的样子：

eg2. 

它所描述的变换的图形描述为：

        这其实是在平面上对一个轴进行的拉伸变换（如蓝色的箭头所示），在图中，蓝色的箭头是一个最主要的变化方向（变化方向可能有不止一个），如果我们想要描述好一个变换，那我们就描述好这个变换主要的变化方向就好了。反过头来看看之前特征值分解的式子，分解得到的D矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）。

        当矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换，这个线性变化可能没法通过图片来表示，但是可以想象，这个变换也同样有很多的变换方向，我们通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向，就可以近似这个矩阵（变换）。也就是之前说的：提取这个矩阵最重要的特征。

        总结：特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。

        奇异值（SVD）分解：

        由于特征值分解有局限性，它的变换的矩阵必须是方阵，所以引入了特征值分解。特征值分解的矩阵可以是任意的方阵。

        任意一个实数m×n矩阵A，存在正交矩阵U和V以及一个对角矩阵，这次表示为Σ，使得A = 。

        分析一下SVD怎么和EVD相对应的：

        我们将一个矩阵A的转置与A相乘，将会得到一个方阵（nxn维），我们用这个方阵求特征值可以得到：

        这里的v就是上面的右奇异向量；

        此外还可以得到，这里的σ就是上面说的奇异值; 

         ,  u就是上面说的左奇异向量。其中ui是Avi方向上的单位向量。

        分析可以用一个2x2的矩阵进行分析：

eg3. 

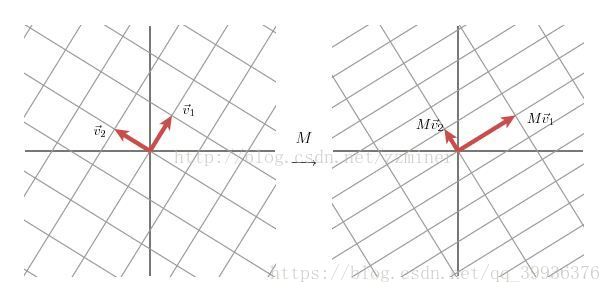
        这就是SVD在2x2矩阵下的几何学本质：对于任意的2x2矩阵，我们能找到一个正交的网格(grid)，它被转换到了另外一个正交网格。

        我们使用向量来描述这个现象：如果我们通过某种方式挑出两个单位向量（unit vector）v₁和v₂，它们是正交的，向量Mv₁ 和Mv₂ 也是正交的。

        我们用u₁和u₂代表向量Mv₁ 和Mv₂ 方向的单位向量，用σ₁ andσ₂代表向量Mv₁ 和Mv₂的长度，它们描述网格在这些方向上的拉伸量。

        因此我们有 ：Mv₁ = σ₁u_{1 ，} Mv₂ = σ₂u_{2 。}

        现在简单说一下矩阵M是如何处理普通向量x的。因为单位向量v₁和v₂是正交的（形成了一规范正交基，orthonomal basis），所以我们有：x = (v₁∙x)v1 + (v2∙x)v2      （注释：x ∙v1 = (v1∙x) v1∙v1 + (v2∙x)v2∙v1 = (v1∙x) *1+0 = v1∙x=x∙v1）

        这意味着  Mx = (v₁∙x)Mv₁ + (v₂∙x)Mv_{2 ，} Mx = (v₁∙x)σ₁u1+ (v₂∙x)σ₂u₂

        由于dot product 操作可以用矩阵转置实现： v∙x = v^Tx ，从而导出 Mx = u₁σ₁v₁^Tx +u₂σ₂v₂^Tx ，M = u₁σ₁v₁^T +u₂σ₂v₂^T         上述表达式可以简写成  M = UΣV^T

        其中U 是由向量u1 和u2（作为列）组成的矩阵, Σ 是对角矩阵，对角线上的值是σ1 和σ2,V 是向量v1和v2(作为列)组成的矩阵。矩阵V的上标T 代表V的矩阵转置。

        上面显示了如何将矩阵M分解为三矩阵的积: V描述在domain中的规范正交基（orthonomal basis），U描述co-domain中的规范正交基，Σ描述在V中的向量在U中拉伸量。

        所以SVD的Idea是：如果我们在向量空间Rⁿ 和R^m上选择正确的基(basis)，每个mxn矩阵均可对角线化(diagonalized)。

        现在我们可以看到一个m×n矩阵A的SVD。这里的变换将带到一个不同的空间。

        奇异值σ跟特征值类似，在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解：

        The SVD and EVD：

        我们的构造展示了如何从对称矩阵的EVD确定A的SVD。相反，很容易从A的SVD恢复的EVD。假设奇异值分解A = 是给出。显然， = 和。现在以任一顺序，Σ和ΣT的乘积是一个平方对角线矩阵，其前k个对角线值是，并且任何剩余的对角线条目等于0。因此， = 是的EVD和是的EVD。所以，在A的任何奇异值分解中，右奇异向量（V的列）必须是的特征向量，左奇异向量（U的列）必须是的特征向量，并且奇异值必须是非零的平方根这两个对称矩阵共有的特征值。因此，在和的多维特征空间中可能的正交变换，SVD中的矩阵V和U是唯一确定的。

        SVD的应用：

        PCA，数据压缩等等

        参考文献： A Singularly Valuable Decomposition: The SVD of a Matrix