《Factorization Machines》 | FM模型及python实现

1 Factorization Machines 原文

2 FM模型

2.1 背景

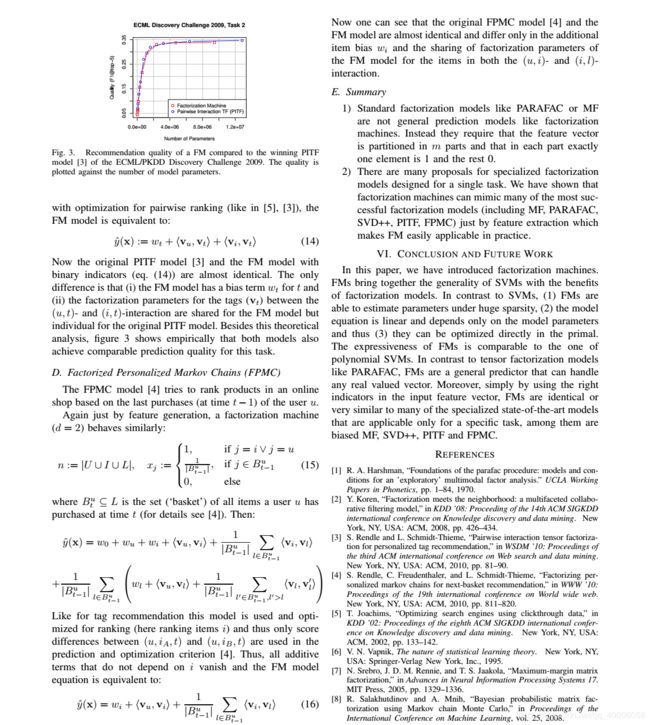
计算广告和推荐系统中，CTR预估是一个非常重要的环节，判断一个item是否应该被推荐要根据CTR预估的点击率进行。CTR预估时，除了单特征以外，往往需要组合特征。

数据经过one-hot编码以后，导致样本数据变得非常稀疏，另外，还导致特征空间变大。为了解决数据稀疏（one-hot coding）情况下，特征如何组合的问题，FM由此诞生。

2.2 ＦＭ模型求解

普通的现行模型，例如逻辑回归，都是单独的考虑各个特征，并没有考虑特征之间的联系。常用模型为：

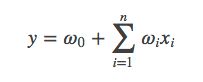
从上式中可以发现，各个特征并没有进行组合，忽略了特征之间的关联。FM模型将特征进行组合，考虑了特征之间的相关关系，模型如下：

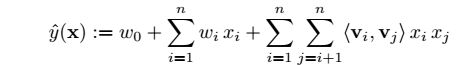
对比两个模型发现，FM比线性模型仅仅多了最后一项。

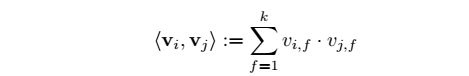
最后一项求解

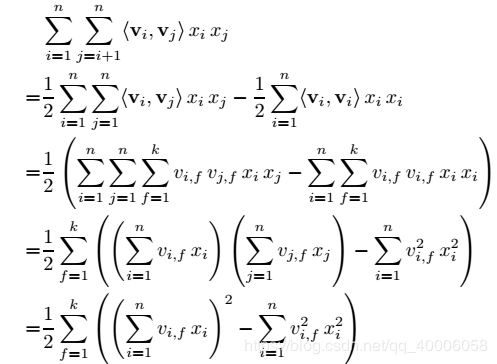
利用SGD对模型参数求解

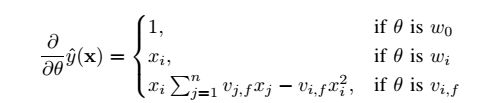
3 python实现

1、实验数据集：movielens，包含四列。【用户ID | 电影ID | 打分 | 时间戳】

2、用到的函数库

from itertools import count # 迭代器
from collections import defaultdict # 使用dict时，如果引用的Key不存在，就会抛出KeyError。如果希望key不存在时，返回一个默认值，就可以用defaultdict
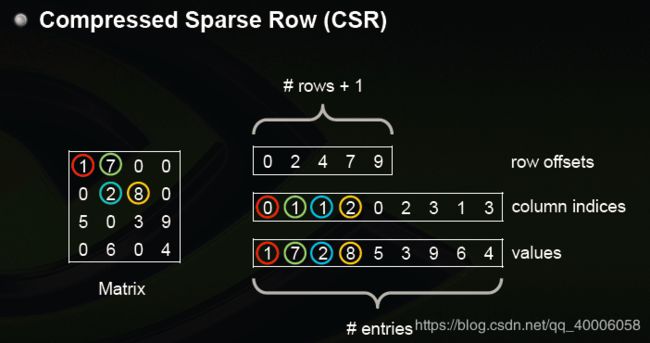
from scipy.sparse import csr # csr_matrix，全名为Compressed Sparse Row，是按行对矩阵进行压缩的。CSR需要三类数据：数值，列号，以及行偏移量。CSR是一种编码的方式，其中，数值与列号的含义，与coo里是一致的。行偏移表示某一行的第一个元素在values里面的起始偏移位置。 
import numpy as np
import pandas as pd
from sklearn.feature_extraction import DictVectorizer
import tensorflow as tf
from tqdm import tqdm_notebook as tqdm # 可以显示循环的进度条的库

3、将数据转换成一个大小为 用户ID数X电影ID数（样本数*特征总数） 的矩阵，使用scipy.sparse中的csr_matrix函数。csr_matrix((data, indices, indptr)第一个参数是数值对应下图中的data，第二个参数是每个数对应的列号column indices，第三个参数是每行的起始的偏移量row offsets。

def vectorize_dic(dic, ix=None, p=None):
    """ 
    Creates a scipy csr matrix from a list of lists (each inner list is a set of values corresponding to a feature) 
    
    parameters:
    -----------
    dic -- dictionary of feature lists. Keys are the name of features
    ix -- index generator (default None)
    p -- dimension of featrure space (number of columns in the sparse matrix) (default None)
    """
    if (ix == None):
        d = count(0)
        ix = defaultdict(lambda: next(d)) 
        
    n = len(list(dic.values())[0]) # num samples
    g = len(list(dic.keys())) # num groups
    nz = n * g # number of non-zeros

    col_ix = np.empty(nz, dtype=int)     
    
    i = 0
    for k, lis in dic.items():     
        # append index el with k in order to prevet mapping different columns with same id to same index
        col_ix[i::g] = [ix[str(el) + str(k)] for el in lis]
        i += 1
        
    row_ix = np.repeat(np.arange(0, n), g)      
    data = np.ones(nz)
    
    if (p == None):
        p = len(ix)
        
    ixx = np.where(col_ix < p)

    return csr.csr_matrix((data[ixx],(row_ix[ixx], col_ix[ixx])), shape=(n, p)), ix

cols = ['user','item','rating','timestamp']

train = pd.read_csv('data/ua.base',delimiter='\t',names = cols)
test = pd.read_csv('data/ua.test',delimiter='\t',names = cols)

x_train,ix = vectorize_dic({'users':train['user'].values,  'items':train['item'].values},n=len(train.index),g=2)

x_test,ix = vectorize_dic({'users':test['user'].values,   'items':test['item'].values},ix,x_train.shape[1],n=len(test.index),g=2)

print(x_train)
y_train = train['rating'].values
y_test = test['rating'].values

x_train = x_train.todense() # toarray returns an ndarray; todense returns a matrix. If you want a matrix, use todense otherwise, use toarray
x_test = x_test.todense()

4、生成器，

def batcher(X_, y_=None, batch_size=-1):
    n_samples = X_.shape[0]

    if batch_size == -1:
        batch_size = n_samples
    if batch_size < 1:
       raise ValueError('Parameter batch_size={} is unsupported'.format(batch_size))

    for i in range(0, n_samples, batch_size):
        upper_bound = min(i + batch_size, n_samples)
        ret_x = X_[i:upper_bound]
        ret_y = None
        if y_ is not None:
            ret_y = y_[i:i + batch_size]
            yield (ret_x, ret_y)

5、估计值计算

n,p = x_train.shape

k = 10

x = tf.placeholder('float',[None,p])

y = tf.placeholder('float',[None,1])

w0 = tf.Variable(tf.zeros([1]))
w = tf.Variable(tf.zeros([p]))

v = tf.Variable(tf.random_normal([k,p],mean=0,stddev=0.01))

#y_hat = tf.Variable(tf.zeros([n,1]))

linear_terms = tf.add(w0,tf.reduce_sum(tf.multiply(w,x),1,keep_dims=True)) # n * 1
pair_interactions = 0.5 * tf.reduce_sum(
    tf.subtract(
        tf.pow(
            tf.matmul(x,tf.transpose(v)),2),
        tf.matmul(tf.pow(x,2),tf.transpose(tf.pow(v,2)))
    ),axis = 1 , keep_dims=True)

y_hat = tf.add(linear_terms,pair_interactions)

6、损失函数计算：损失函数除了平方损失外，还加了l2正则项，并使用梯度下降法进行参数的更新：

lambda_w = tf.constant(0.001,name='lambda_w')
lambda_v = tf.constant(0.001,name='lambda_v')

l2_norm = tf.reduce_sum(
    tf.add(
        tf.multiply(lambda_w,tf.pow(w,2)),
        tf.multiply(lambda_v,tf.pow(v,2))
    )
)

error = tf.reduce_mean(tf.square(y-y_hat))
loss = tf.add(error,l2_norm)

train_op = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(loss)

7、模型训练

epochs = 10
batch_size = 1000

# Launch the graph
init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)

    for epoch in tqdm(range(epochs), unit='epoch'):
        perm = np.random.permutation(x_train.shape[0]) # 函数shuffle与permutation都是对原来的数组进行重新洗牌（即随机打乱原来的元素顺序）；区别在于shuffle直接在原来的数组上进行操作，改变原来数组的顺序，无返回值。而permutation不直接在原来的数组上进行操作，而是返回一个新的打乱顺序的数组，并不改变原来的数组。
        # iterate over batches
        for bX, bY in batcher(x_train[perm], y_train[perm], batch_size):
            _,t = sess.run([train_op,loss], feed_dict={x: bX.reshape(-1, p), y: bY.reshape(-1, 1)})
            print(t)


    errors = []
    for bX, bY in batcher(x_test, y_test):
        errors.append(sess.run(error, feed_dict={x: bX.reshape(-1, p), y: bY.reshape(-1, 1)}))
        print(errors)
    RMSE = np.sqrt(np.array(errors).mean())
    print (RMSE)