深度知识追踪入门

背景介绍

知识追踪（Knowledge Tracing）是根据学生过去的答题情况对学生的知识掌握情况进行建模，从而得到学生当前知识状态表示的一种技术，早期的知识追踪模型都是依赖于一阶马尔科夫模型，例如贝叶斯知识追踪（Bayesian Knowledge Tracing）。将深度学习的方法引入知识追踪最早出现于发表在NeurIPS 2015上的一篇论文《Deep Knowledge Tracing》，作者来自斯坦福大学。在这篇论文中，作者提出了使用深度知识追踪（Deep Knowledge Tracing）的概念，利用RNN对学生的学习情况进行建模，之后引出了一系列工作，2019年已经有使用Transformer代替RNN和LSTM并且达到了SOTA的论文。

由于深度学习并不需要人类教会模型不同题目的难易、考核内容等特定的知识，避免了大量的手工标注特征工作量，而且在互联网在线教育行业兴起后，拥有了海量的学生答题记录，这些答题记录就能教会模型将题库中成千上万条题目encode为一个向量，并且能类似于word2vec那样找出题目之间的关联。因此之后各种AI+教育、个性化、智能化教育的概念也火了起来。不过截止目前深度知识追踪仍然只是一个小领域，业界应该是做了不少工作的，但因为每个公司教育数据的私密性，不同公司数据的多样性，导致了数据集不公开，方法也大多不通用的情况，因此我们并不太能了解到那些在线教育巨头背后的AI技术，至于学界，论文大多发表在教育数据挖掘国际会议上（Educational Data Mining）。本文简单介绍深度知识追踪，给有兴趣入门的同学的作参考。

任务定义

知识追踪的任务是根据学生的答题记录，通常是一个时间序列，有些业务场景下是与时间无关的，建模得到学生的知识掌握状态，从而能准确预测其未来的答题情况，并依据此为未来的智能化出题做参考，避免给学生出太难或太简单的题目。具体上，假设一个学生的答题记录为$x_0,x_1,...,x_t$，我们要去预测下一个交互的情况$x_{t+1}$，通常一次交互$x_t=(q_t,a_t)$，$q_t$代表该学生回答题目$a_t$的正误情况。简单的来说就是知道了学生答了一系列题目，也都知道他都回答对了没，现在我要从题库里再抽一题给他，让模型预测预测他能不能答对，答对的概率是多少，那么如果模型给出的概率是1，代表这题对他来说是太简单了，如果给出的概率为0，就代表这题可能太难了，他八成是做不出来的。

模型

上面说了，Deep Knowledge Tracing这篇论文是用了RNN来把答题记录当做平常的时间序列来建模，至于RNN，下面简单列个公式表示一下，相信入门过NLP的同学都是认识RNN的。
$$\begin{array}{rl}{\mathbf{h}}_t& =\tanh \left({\mathbf{W}}_{hx}{\mathbf{x}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1}+{\mathbf{b}}_h\right)\\ {\mathbf{y}}_t& =\sigma \left({\mathbf{W}}_{yh}{\mathbf{h}}_t+{\mathbf{b}}_y\right)\end{array}$$

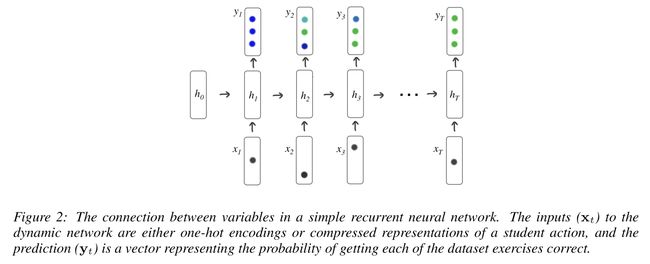
模型的输入和输出

假设数据集有$M$道题目，我们让$x_t$为one-hot encoding，由于$a_t\in R^M$，$q_t\in \{0,1\}$，那么$x_t\in R^{2M}$，即针对题目$a_t$有答对和答错两种不同的状态，所以one-hot的长度是2M。这时候很自然就能想到使用NLP中常用的Embedding，将每个one-hot向量通过embedding转为一个维度小得多的向量$n_{a_t,q_t}\in R^N$，$N<<M$，这样每道题目就可以初始化为一个随机的低维向量表征，在之后的数据集上进行训练。

每个时间步，模型输入$x_t$，输出$y_t\in R^M$，维度与题库大小相同，代表着学生答对每道题目的概率。我们根据$y_t$可以选出下一题$a_{t+1}$的正确概率$p_{t+1}$，再和真实的标签$q_{t+1}$求交叉熵损失函数即：
$$L=\sum _t\ell \left({\mathbf{y}}^T\delta \left(q_{t+1}\right),a_{t+1}\right)$$
其中$\ell$代表交叉熵损失函数，$\delta$代表one-hot编码。

Optimization

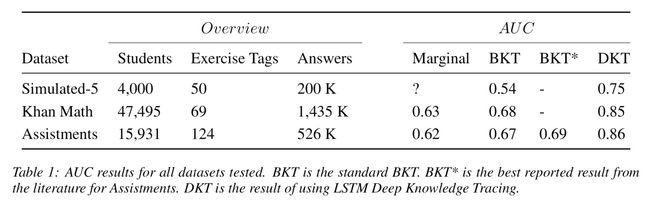
为了防止过拟合，在使用中间的隐层状态$h_t$通过dense层得到$y_t$时加了dropout，同时在反向传播时为了避免梯度爆炸，增加了梯度裁剪，评价指标使用的是AUC（area under the curve）。

实验结果

作者在三个数据集上进行了实验，在当时都达到了SOTA

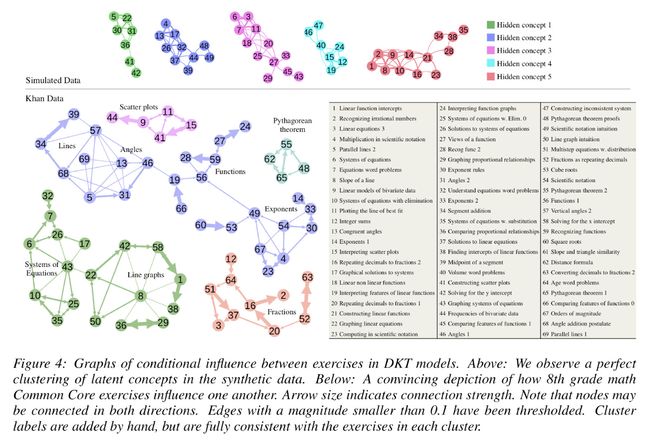
并且在Khan Data和Simulated Data上做了可视化，发现RNN成功捕捉到了相似题目之间的关联，将同一概念下的题目如函数、几何聚到了一起。

优缺点

优点

1. 能根据学生最近的答题情况记录较长时间的知识情况。
2. 能根据每次答题更新知识状态，只需要保存上一个隐层状态，不需要重复计算，适合线上部署。
3. 不需要domain specific的知识，对任何用户答题数据集都适用。
4. 能够自动捕捉相似题目之间的关联。

缺点

1. 当答题序列被打乱时，模型输出的结果波动大，即相同的题目和相同的回答，当答题顺序不一致时，得到的知识状态不同。
2. 由于上述问题，且学生在答题过程中对知识的掌握程度不一定具有连续一致性，导致对学生知识状态的预测受顺序影响发生偏差。
3. 黑盒，有时会出现第一题答对导致对之后的预测概率都偏高，而第一题答错对之后的预测概率都偏低的奇怪情况。

总结

介绍的这篇论文是深度知识追踪的开山之作，之后有许多论文对它进行的完善，几个具有代表性的是：

• How Deep is Knowledge Tracing?
• Going Deeper with Deep Knowledge Tracing
• Incorporating Rich Features into Deep Knowledge Tracing
• Addressing Two Problems in Deep Knowledge Tracing via Prediction-Consistent Regularization
• A Self-Attentive model for Knowledge Tracing

参考文献：

[1] Piech, C. et al. Deep knowledge tracing. in Advances in Neural Information Processing Systems 505–513 (2015).