Python--基于卷积神经网络的图像分类

什么是过拟合

过拟合是指为了得到一致假设而使假设变得过度严格。避免过拟合是分类器设计中的一个核心任务。通常采用增大数据量和测试样本集的方法对分类器性能进行评价。

定义
给定一个假设空间H，一个假设h属于H，如果存在其他的假设h’属于H,使得在训练样例上h的错误率比h’小，但在整个实例分布上h’比h的错误率小，那么就说假设h过度拟合训练数据。

一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。出现这种现象的主要原因是训练数据中存在噪音或者训练数据太少

什么是数据增强

数据增强
数据增强主要用来防止过拟合，用于dataset较小的时候。
当然除了数据增强，还有正则项/dropout等方式可以防止过拟合。那接下来讨论下常见的数据增强方法。

1）随机旋转
随机旋转一般情况下是对输入图像随机旋转[0,360)
2）随机裁剪
随机裁剪是对输入图像随机切割掉一部分
3）色彩抖动
色彩抖动指的是在颜色空间如RGB中，每个通道随机抖动一定的程度。在实际的使用中，该方法不常用，在很多场景下反而会使实验结果变差
4）高斯噪声
是指在图像中随机加入少量的噪声。该方法对防止过拟合比较有效，这会让神经网络不能拟合输入图像的所有特征
5）水平翻转
6）竖直翻转

python代码

import keras
keras.__version__

＃ 对小数据集使用卷积网络

本笔记本包含[ Python深度学习 ]（https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff）第5章第2节中提供的代码示例。请注意，原始文本具有更多内容，尤其是进一步的说明和附图：在本笔记本中，您将仅找到源代码和相关注释。

在小数据集上从头训练convnet

通常只需要很少的数据就可以训练图像分类模型，这是一种常见的情况，如果您在专业环境中进行计算机视觉，您可能会在实践中遇到自己。

具有“少量”样本可能意味着从几百到几万张图像。作为一个实际示例，我们将重点关注在包含4000张猫和狗（2000只猫，2000只狗）图片的数据集中，将图像分类为“狗”还是“猫”。我们将使用2000 张图片进行培训，使用1000张图片进行验证，最后使用1000张图片进行测试。

在本节中，我们将介绍解决该问题的一种基本策略：从头开始训练我们拥有的少量数据的新模型。我们将首先对2000个培训样本进行一次简单的convnet培训，而无需进行任何正则化，从而为可以实现的目标设定基准。这将使我们的分类精度达到71％。到那时，我们的主要问题将是过度拟合。然后，我们将介绍数据增强，这是一种缓解计算机视觉过度拟合的强大技术。通过利用数据增强，我们将改善我们的网络以达到82％的准确性。

在下一部分中，我们将介绍另外两种将深度学习应用于小型数据集的基本技术：*
使用预先训练的网络进行特征提取*（这将使我们的准确度达到90％至93％），并且很好-调整预训练的网络（这将使我们的最终精度达到95％）。这三种策略一起使用-从头开始训练一个小型模型，使用预训练的模型进行特征提取以及对预训练的模型进行微调-将构成您将来解决使用小工具进行计算机视觉问题的工具箱数据集。

深度学习与小数据问题的相关性

有时您会听到深度学习仅在有大量数据可用时才起作用。这在一定程度上是正确的：深度学习的一个基本特征是，它能够自己在训练数据中找到有趣的特征，而无需进行人工特征工程，而只有在有大量训练示例时才能实现可用。对于输入样本非常高维的问题（例如图像），尤其如此。

但是，构成样本的“批次”是相对的-对于初学者而言，与您要训练的网络的大小和深度有关。仅用几十个样本就不可能训练卷积网络来解决复杂的问题，但是如果模型很小且规则良好，并且任务很简单，那么数百个就足够了。因为卷积学习局部不变的平移特征，所以它们在感知问题上的数据效率很高。尽管相对缺乏数据，但在非常小的图像数据集上从头开始训练卷积网络仍会产生合理的结果，而无需任何自定义特征工程。您将在本节中看到这一点。

但是更重要的是，深度学习模型本质上具有高度的可重复性：例如，您可以采用在大规模数据集上训练的图像分类或语音到文本模型，然后仅需很小的更改就可以将其重用于一个明显不同的问题。具体来说，在计算机视觉的情况下，许多预先训练的模型（通常在ImageNet数据集上进行训练）现在可以公开下载，并且可以用于从很少的数据中引导功能强大的视觉模型。这就是我们在下一节中要做的。

现在，让我们开始使用数据。

下载数据

我们将使用的猫与狗数据集未与Keras打包在一起。Kavgle.com 在2013年底的计算机视觉竞赛中提供了它，当时卷积网络还不是很主流。您可以下载原始数据集：https://www.kaggle.com/c/dogs-vs-cats/data（你需要创建一个帐户Kaggle如果您还没有一个-不要”不用担心，这个过程很轻松）。

毫不奇怪，2013年的猫对狗Kaggle比赛由使用卷积网络的参赛者赢得。最好的输入可以达到95％的准确性。在我们自己的示例中，即使我们将在少于竞争对手可用数据的10％的数据上训练模型，也将相当接近此准确性（在下一部分中）。该原始数据集包含25,000张猫和狗的图像（每类12,500张），并且大小为543MB（压缩）。下载并解压缩后，我们将创建一个包含三个子集的新数据集：一个训练集，每个类别有1000个样本；一个验证集，每个类别有500个样本；最后是一个测试集，每个类别有500个样本。

这是执行此操作的几行代码：

import os, shutil

# The path to the directory where the original
# dataset was uncompressed
original_dataset_dir = './mycatdog'

# The directory where we will
# store our smaller dataset
base_dir = './out1'
os.mkdir(base_dir)

# Directories for our training,
# validation and test splits
train_dir = os.path.join(base_dir, 'train')
os.mkdir(train_dir)
validation_dir = os.path.join(base_dir, 'validation')
os.mkdir(validation_dir)
test_dir = os.path.join(base_dir, 'test')
os.mkdir(test_dir)

# Directory with our training cat pictures
train_cats_dir = os.path.join(train_dir, 'cats')
os.mkdir(train_cats_dir)

# Directory with our training dog pictures
train_dogs_dir = os.path.join(train_dir, 'dogs')
os.mkdir(train_dogs_dir)

# Directory with our validation cat pictures
validation_cats_dir = os.path.join(validation_dir, 'cats')
os.mkdir(validation_cats_dir)

# Directory with our validation dog pictures
validation_dogs_dir = os.path.join(validation_dir, 'dogs')
os.mkdir(validation_dogs_dir)

# Directory with our validation cat pictures
test_cats_dir = os.path.join(test_dir, 'cats')
os.mkdir(test_cats_dir)

# Directory with our validation dog pictures
test_dogs_dir = os.path.join(test_dir, 'dogs')
os.mkdir(test_dogs_dir)

# Copy first 1000 cat images to train_cats_dir
fnames = ['cat.{}.jpg'.format(i) for i in range(10)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(train_cats_dir, fname)
    shutil.copyfile(src, dst)

# Copy next 500 cat images to validation_cats_dir
fnames = ['cat.{}.jpg'.format(i) for i in range(10, 20)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(validation_cats_dir, fname)
    shutil.copyfile(src, dst)
    
# Copy next 500 cat images to test_cats_dir
fnames = ['cat.{}.jpg'.format(i) for i in range(20, 30)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(test_cats_dir, fname)
    shutil.copyfile(src, dst)
    
# Copy first 1000 dog images to train_dogs_dir
fnames = ['dog.{}.jpg'.format(i) for i in range(10)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(train_dogs_dir, fname)
    shutil.copyfile(src, dst)
    
# Copy next 500 dog images to validation_dogs_dir
fnames = ['dog.{}.jpg'.format(i) for i in range(10, 20)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(validation_dogs_dir, fname)
    shutil.copyfile(src, dst)
    
# Copy next 500 dog images to test_dogs_dir
fnames = ['dog.{}.jpg'.format(i) for i in range(20, 30)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(test_dogs_dir, fname)
    shutil.copyfile(src, dst)

作为健全性检查，让我们计算一下每个训练分组（训练/验证/测试）中有多少张图片：

print('total training cat images:', len(os.listdir(train_cats_dir)))

 总训练猫的图像：10

print('total training dog images:', len(os.listdir(train_dogs_dir)))

 总训练狗的图像：10

print('total validation cat images:', len(os.listdir(validation_cats_dir)))

 总验证猫的图像：10

print('total validation dog images:', len(os.listdir(validation_dogs_dir)))

 总验证狗的图像：10

print('total test cat images:', len(os.listdir(test_cats_dir)))

 总验证狗的图像：10

print('total test dog images:', len(os.listdir(test_dogs_dir)))

 总验证狗的图像：10

所以我们确实有2000个训练图像，然后是1000个验证图像和1000个测试图像。在每个分组中，每个类别中的样本数均相同：这是一个平衡的二进制分类问题，这意味着分类准确性将是成功与否的适当衡量标准。

建立我们的网络

在上一个示例中，我们已经为MNIST构建了一个小型卷积网络，因此您应该熟悉它们。我们将重复使用相同的基本结构：我们convnet将是交替的堆栈Conv2D（带RELU激活）和MaxPooling2D层。

然而，由于我们处理的是更大的图像和更复杂的问题，我们将尽我们的网络因此大：它有一个更Conv2D + MaxPooling2D阶段。这既可以增加网络的容量，又可以进一步减小要素图的大小，这样当我们到达“扁平化”层时，它们就不会太大。在这里，由于我们从大小为150x150的输入（某种程度上是任意选择）开始，因此我们在“展平”层之前得到了大小为7x7的要素图。

请注意，特征图的深度在网络中逐渐增加（从32到128），而特征图的大小在减小（从148x148到7x7）。在几乎所有的卷积网络中都会看到这种模式。

由于我们正在攻击二进制分类问题，因此我们以单个单元（大小为1 的“密集”层）和“ sigmoid ”激活来结束网络。该单元将对网络正在查看一个或另一个类别的概率进行编码。

from keras import layers
from keras import models

model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu',
                        input_shape=(150, 150, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

让我们来看看要素地图的尺寸是如何随每个连续图层而变化的：

model.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_1 (Conv2D)            (None, 148, 148, 32)      896       
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 74, 74, 32)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 72, 72, 64)        18496     
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 36, 36, 64)        0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 34, 34, 128)       73856     
_________________________________________________________________
max_pooling2d_3 (MaxPooling2 (None, 17, 17, 128)       0         
_________________________________________________________________
conv2d_4 (Conv2D)            (None, 15, 15, 128)       147584    
_________________________________________________________________
max_pooling2d_4 (MaxPooling2 (None, 7, 7, 128)         0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 6272)              0         
_________________________________________________________________
dense_1 (Dense)              (None, 512)               3211776   
_________________________________________________________________
dense_2 (Dense)              (None, 1)                 513       
=================================================================
Total params: 3,453,121
Trainable params: 3,453,121
Non-trainable params: 0
_________________________________________________________________

对于我们的编译步骤，我们将与去RMSprop优化如常。由于我们以单个S形单位结束网络，因此我们将使用二进制交叉熵作为损失（提醒一下，请参阅第4章第5节中的表格，以了解在各种情况下要使用的损失函数的备忘单）。

from keras import optimizers

model.compile(loss='binary_crossentropy',
              optimizer=optimizers.RMSprop(lr=1e-4),
              metrics=['acc'])

数据预处理

如您现在所知，在将数据馈入我们的网络之前，应将其格式化为经过适当预处理的浮点张量。当前，我们的数据以JPEG文件的形式位于驱动器上，因此将其放入网络的步骤大致如下：

• 读取图片文件。* 将JPEG内容解码为RBG像素网格。* 将它们转换为浮点张量。* 将像素值（0到255之间）重新缩放为[0，1]间隔（如您所知，神经网络更喜欢处理较小的输入值）。

似乎有些令人生畏，但值得庆幸的是Keras拥有实用程序来自动完成这些步骤。Keras与图像的模块处理辅助工具，位于keras.preprocessing.image。特别是，它包含的类ImageDataGenerator，它允许快速设置Python生成器，可以自动打开图像文件在磁盘上为预处理张量的批次。这就是我们将在这里使用的。

from keras.preprocessing.image import ImageDataGenerator

# All images will be rescaled by 1./255
train_datagen = ImageDataGenerator(rescale=1./255)
test_datagen = ImageDataGenerator(rescale=1./255)

train_generator = train_datagen.flow_from_directory(
        # This is the target directory
        train_dir,
        # All images will be resized to 150x150
        target_size=(150, 150),
        batch_size=20,
        # Since we use binary_crossentropy loss, we need binary labels
        class_mode='binary')

validation_generator = test_datagen.flow_from_directory(
        validation_dir,
        target_size=(150, 150),
        batch_size=20,
        class_mode='binary')

Found 20 images belonging to 2 classes.
Found 20 images belonging to 2 classes.

实测值20个图像属于2类。 找到20个属于2类的图像。让我们看一看这些生成器之一的输出：它生成一批150x150 RGB图像（形状为（（20，150，150，3））和二进制标签（形状为（（20，））））。每个批次中的样本数20（批次大小）。请注意，生成器无限期地产生这些批处理：它只是无限循环地遍历目标文件夹中存在的图像。因此，我们需要在某个时候“中断”迭代循环。

for data_batch, labels_batch in train_generator:
    print('data batch shape:', data_batch.shape)
    print('labels batch shape:', labels_batch.shape)
    break

data batch shape: (20, 150, 150, 3)
labels batch shape: (20,)

让我们使用生成器将模型拟合到数据。我们用它做fit_generator方法，相当于适合数据生成像我们这样。它期望Python生成器作为第一个参数，像我们一样，将无限期地产生大量输入和目标。由于数据是无休止地生成的，因此生成器需要在声明一个时期之前知道示例要从生成器中抽取多少个样本。这是角色steps_per_epoch说法：具有延伸后steps_per_epoch从批次发电机，具有运行后，即steps_per_epoch梯度下降步骤，拟合过程将进入下一个时代。在我们的示例中，批次为20个样本，因此将需要100个批次，直到我们看到我们的目标是2000个样本。期望该生成器无休止地生成验证数据的批次，因此您还应该指定validation_steps参数，该参数告诉过程从验证生成器中抽取多少批次进行评估。

history = model.fit_generator(
      train_generator,
      steps_per_epoch=80,
      epochs=30,
      validation_data=validation_generator,
      validation_steps=50)

Epoch 1/30
80/80 [==============================] - 48s 605ms/step - loss: 0.2500 - acc: 0.9200 - val_loss: 0.6217 - val_acc: 0.6000
Epoch 2/30
80/80 [==============================] - 45s 560ms/step - loss: 0.0012 - acc: 1.0000 - val_loss: 1.0331 - val_acc: 0.5500
Epoch 3/30
80/80 [==============================] - 46s 573ms/step - loss: 6.8918e-06 - acc: 1.0000 - val_loss: 1.5310 - val_acc: 0.5500
Epoch 4/30
80/80 [==============================] - 42s 529ms/step - loss: 1.1915e-07 - acc: 1.0000 - val_loss: 1.9704 - val_acc: 0.5500
Epoch 5/30
80/80 [==============================] - 42s 525ms/step - loss: 1.6333e-08 - acc: 1.0000 - val_loss: 2.2112 - val_acc: 0.5500
Epoch 6/30
80/80 [==============================] - 41s 512ms/step - loss: 1.1360e-08 - acc: 1.0000 - val_loss: 2.2967 - val_acc: 0.5500
Epoch 7/30
80/80 [==============================] - 41s 517ms/step - loss: 1.0666e-08 - acc: 1.0000 - val_loss: 2.3855 - val_acc: 0.5500
Epoch 8/30
80/80 [==============================] - 41s 517ms/step - loss: 1.0514e-08 - acc: 1.0000 - val_loss: 2.4290 - val_acc: 0.5500
Epoch 9/30
80/80 [==============================] - 41s 508ms/step - loss: 1.0513e-08 - acc: 1.0000 - val_loss: 2.4661 - val_acc: 0.5500
Epoch 10/30
80/80 [==============================] - 40s 505ms/step - loss: 1.0506e-08 - acc: 1.0000 - val_loss: 2.4857 - val_acc: 0.5500
Epoch 11/30
80/80 [==============================] - 40s 506ms/step - loss: 1.0329e-08 - acc: 1.0000 - val_loss: 2.5173 - val_acc: 0.5500
Epoch 12/30
80/80 [==============================] - 43s 537ms/step - loss: 1.0348e-08 - acc: 1.0000 - val_loss: 2.5537 - val_acc: 0.5500
Epoch 13/30
80/80 [==============================] - 47s 583ms/step - loss: 1.0316e-08 - acc: 1.0000 - val_loss: 2.5501 - val_acc: 0.5500
Epoch 14/30
80/80 [==============================] - 44s 545ms/step - loss: 1.0264e-08 - acc: 1.0000 - val_loss: 2.5886 - val_acc: 0.5500
Epoch 15/30
80/80 [==============================] - 40s 506ms/step - loss: 1.0294e-08 - acc: 1.0000 - val_loss: 2.5845 - val_acc: 0.5500
Epoch 16/30
80/80 [==============================] - 43s 537ms/step - loss: 1.0186e-08 - acc: 1.0000 - val_loss: 2.6096 - val_acc: 0.5500
Epoch 17/30
80/80 [==============================] - 45s 558ms/step - loss: 1.0184e-08 - acc: 1.0000 - val_loss: 2.6252 - val_acc: 0.5500
Epoch 18/30
80/80 [==============================] - 43s 538ms/step - loss: 1.0217e-08 - acc: 1.0000 - val_loss: 2.6405 - val_acc: 0.5500
Epoch 19/30
80/80 [==============================] - 42s 520ms/step - loss: 1.0199e-08 - acc: 1.0000 - val_loss: 2.6236 - val_acc: 0.5500
Epoch 20/30
80/80 [==============================] - 46s 575ms/step - loss: 9.8130e-09 - acc: 1.0000 - val_loss: 2.6521 - val_acc: 0.5500
Epoch 21/30
80/80 [==============================] - 43s 542ms/step - loss: 1.0129e-08 - acc: 1.0000 - val_loss: 2.6751 - val_acc: 0.5500
Epoch 22/30
80/80 [==============================] - 44s 550ms/step - loss: 1.0231e-08 - acc: 1.0000 - val_loss: 2.6755 - val_acc: 0.5500
Epoch 23/30
80/80 [==============================] - 42s 530ms/step - loss: 1.0166e-08 - acc: 1.0000 - val_loss: 2.6928 - val_acc: 0.5500
Epoch 24/30
80/80 [==============================] - 44s 552ms/step - loss: 1.0187e-08 - acc: 1.0000 - val_loss: 2.7008 - val_acc: 0.5500
Epoch 25/30
80/80 [==============================] - 43s 536ms/step - loss: 1.0173e-08 - acc: 1.0000 - val_loss: 2.7132 - val_acc: 0.5500
Epoch 26/30
80/80 [==============================] - 40s 502ms/step - loss: 1.0042e-08 - acc: 1.0000 - val_loss: 2.7103 - val_acc: 0.5500
Epoch 27/30
80/80 [==============================] - 41s 512ms/step - loss: 1.0207e-08 - acc: 1.0000 - val_loss: 2.7195 - val_acc: 0.5500
Epoch 28/30
80/80 [==============================] - 44s 554ms/step - loss: 1.0174e-08 - acc: 1.0000 - val_loss: 2.7336 - val_acc: 0.5500
Epoch 29/30
80/80 [==============================] - 41s 511ms/step - loss: 1.0177e-08 - acc: 1.0000 - val_loss: 2.7431 - val_acc: 0.5500
Epoch 30/30
80/80 [==============================] - 40s 501ms/step - loss: 1.0213e-08 - acc: 1.0000 - val_loss: 2.7475 - val_acc: 0.5500

在培训后，始终保存您的模型是一个好的做法：

model.save('cats_and_dogs_small_1.h5')

让我们在培训和验证数据上绘制模型的损失和准确性：

import matplotlib.pyplot as plt

acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(len(acc))

plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()

plt.figure()

plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()

plt.show()

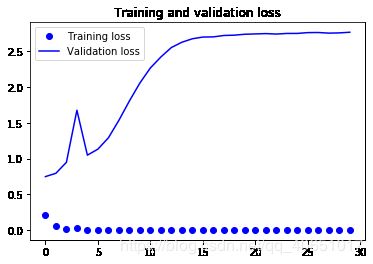
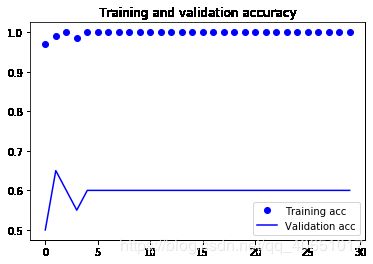
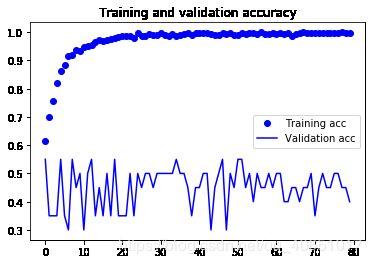
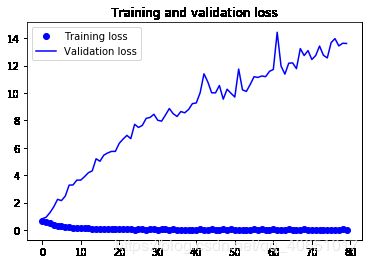
这些曲线图具有过度拟合的特点。我们的训练精度随着时间线性增加，直到接近100%，而我们的

验证准确度暂停在70-72%。我们的验证损失在五个阶段后达到最小，然后停滞，而培训损失

一直线性递减直到接近0。

因为我们只有相对较少的训练样本（2000年），所以过度拟合将是我们最关心的问题。你已经知道

有助于缓解过度拟合的技术数量，如辍学和体重衰减（L2正则化）。我们现在要

介绍一种新的，专门针对计算机视觉的，在使用深度学习模型处理图像时几乎普遍使用的：*数据

增强*。

使用数据扩充

过度拟合是由于样本太少而无法学习，使得我们无法训练一个能够推广到新数据的模型。

给定无限的数据，我们的模型将暴露在手头数据分布的所有可能方面：我们永远不会过度拟合。数据

增强采用的方法是从现有的训练样本中生成更多的训练数据，通过一个数字“增强”样本

产生可信的图像的随机变换。我们的目标是在训练的时候，我们的模型永远不会看到完全一样的结果

想象两次。这有助于模型暴露于数据的更多方面，并更好地进行泛化。

在Keras中，这可以通过配置对ImageDataGenerator读取的图像执行的一些随机转换来完成实例。让我们从一个例子开始：

datagen = ImageDataGenerator(
      rotation_range=40,
      width_shift_range=0.2,
      height_shift_range=0.2,
      shear_range=0.2,
      zoom_range=0.2,
      horizontal_flip=True,
      fill_mode='nearest')

这些只是一些可用的选项（有关更多信息，请参阅Keras文档）。让我们快速回顾一下刚才写的：

*“rotation_range”是一个以度（0-180）为单位的值，在这个范围内可以随机旋转图片。
缩放范围”用于在图片内随机缩放。水平翻转”是指在没有水平假设的情况下，将一半图像随机地水平翻转不对称（如真实世界的图片）。填充模式”是用于填充新创建的像素的策略，可以在旋转或宽度/高度移动后显示。
让我们看看我们的增强图像：

# This is module with image preprocessing utilities
from keras.preprocessing import image

fnames = [os.path.join(train_cats_dir, fname) for fname in os.listdir(train_cats_dir)]

# We pick one image to "augment"
img_path = fnames[3]

# Read the image and resize it
img = image.load_img(img_path, target_size=(150, 150))

# Convert it to a Numpy array with shape (150, 150, 3)
x = image.img_to_array(img)

# Reshape it to (1, 150, 150, 3)
x = x.reshape((1,) + x.shape)

# The .flow() command below generates batches of randomly transformed images.
# It will loop indefinitely, so we need to `break` the loop at some point!
i = 0
for batch in datagen.flow(x, batch_size=1):
    plt.figure(i)
    imgplot = plt.imshow(image.array_to_img(batch[0]))
    i += 1
    if i % 4 == 0:
        break

plt.show()

如果我们使用这种数据增强配置训练一个新网络，我们的网络将永远不会看到两次相同的输入。但是，输入它所看到的仍然是高度相关的，因为它们来自于少量的原始图像——我们无法产生新的信息，我们只能重新混合现有的信息。因此，这可能还不足以完全摆脱过度装修。继续战斗过度拟合，我们还将在密连接分类器之前向模型添加一个退出层：

model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu',
                        input_shape=(150, 150, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dropout(0.5))
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(loss='binary_crossentropy',
              optimizer=optimizers.RMSprop(lr=1e-4),
              metrics=['acc'])

让我们使用数据扩充和退出来训练我们的网络：

train_datagen = ImageDataGenerator(
    rescale=1./255,
    rotation_range=40,
    width_shift_range=0.2,
    height_shift_range=0.2,
    shear_range=0.2,
    zoom_range=0.2,
    horizontal_flip=True,)

# Note that the validation data should not be augmented!
test_datagen = ImageDataGenerator(rescale=1./255)

train_generator = train_datagen.flow_from_directory(
        # This is the target directory
        train_dir,
        # All images will be resized to 150x150
        target_size=(150, 150),
        batch_size=32,
        # Since we use binary_crossentropy loss, we need binary labels
        class_mode='binary')

validation_generator = test_datagen.flow_from_directory(
        validation_dir,
        target_size=(150, 150),
        batch_size=32,
        class_mode='binary')

history = model.fit_generator(
      train_generator,
      steps_per_epoch=50,
      epochs=80,
      validation_data=validation_generator,
      validation_steps=50)

Found 20 images belonging to 2 classes.
Found 20 images belonging to 2 classes.
Epoch 1/80
50/50 [==============================] - 29s 573ms/step - loss: 0.6646 - acc: 0.6150 - val_loss: 0.8158 - val_acc: 0.5500
Epoch 2/80
50/50 [==============================] - 29s 587ms/step - loss: 0.5737 - acc: 0.6990 - val_loss: 0.9219 - val_acc: 0.3500
Epoch 3/80
50/50 [==============================] - 32s 638ms/step - loss: 0.4845 - acc: 0.7580 - val_loss: 1.2549 - val_acc: 0.3500
Epoch 4/80
50/50 [==============================] - 32s 635ms/step - loss: 0.3809 - acc: 0.8210 - val_loss: 1.6812 - val_acc: 0.3500
Epoch 5/80
50/50 [==============================] - 30s 594ms/step - loss: 0.3138 - acc: 0.8610 - val_loss: 2.2329 - val_acc: 0.5500
Epoch 6/80
50/50 [==============================] - 29s 577ms/step - loss: 0.2694 - acc: 0.8830 - val_loss: 2.1424 - val_acc: 0.3500
Epoch 7/80
50/50 [==============================] - 31s 630ms/step - loss: 0.2192 - acc: 0.9170 - val_loss: 2.4715 - val_acc: 0.3000
Epoch 8/80
50/50 [==============================] - 35s 696ms/step - loss: 0.1949 - acc: 0.9210 - val_loss: 3.2708 - val_acc: 0.5500
Epoch 9/80
50/50 [==============================] - 29s 589ms/step - loss: 0.1587 - acc: 0.9380 - val_loss: 3.2843 - val_acc: 0.4500
Epoch 10/80
50/50 [==============================] - 29s 581ms/step - loss: 0.1644 - acc: 0.9340 - val_loss: 3.6380 - val_acc: 0.5000
Epoch 11/80
50/50 [==============================] - 30s 605ms/step - loss: 0.1490 - acc: 0.9470 - val_loss: 3.6353 - val_acc: 0.3000
Epoch 12/80
50/50 [==============================] - 31s 617ms/step - loss: 0.1269 - acc: 0.9520 - val_loss: 3.8901 - val_acc: 0.5000
Epoch 13/80
50/50 [==============================] - 32s 636ms/step - loss: 0.1205 - acc: 0.9560 - val_loss: 4.1789 - val_acc: 0.5500
Epoch 14/80
50/50 [==============================] - 33s 655ms/step - loss: 0.0848 - acc: 0.9670 - val_loss: 4.3144 - val_acc: 0.3500
Epoch 15/80
50/50 [==============================] - 30s 600ms/step - loss: 0.0801 - acc: 0.9710 - val_loss: 5.1957 - val_acc: 0.4500
Epoch 16/80
50/50 [==============================] - 33s 655ms/step - loss: 0.0832 - acc: 0.9690 - val_loss: 5.0150 - val_acc: 0.3500
Epoch 17/80
50/50 [==============================] - 32s 635ms/step - loss: 0.0747 - acc: 0.9740 - val_loss: 5.4591 - val_acc: 0.5000
Epoch 18/80
50/50 [==============================] - 31s 630ms/step - loss: 0.0741 - acc: 0.9750 - val_loss: 5.6205 - val_acc: 0.3500
Epoch 19/80
50/50 [==============================] - 30s 609ms/step - loss: 0.0583 - acc: 0.9800 - val_loss: 5.7334 - val_acc: 0.5500
Epoch 20/80
50/50 [==============================] - 30s 601ms/step - loss: 0.0773 - acc: 0.9830 - val_loss: 5.7338 - val_acc: 0.3500
Epoch 21/80
50/50 [==============================] - 30s 603ms/step - loss: 0.0353 - acc: 0.9880 - val_loss: 6.3216 - val_acc: 0.3500
Epoch 22/80
50/50 [==============================] - 30s 603ms/step - loss: 0.0422 - acc: 0.9850 - val_loss: 6.6349 - val_acc: 0.3500
Epoch 23/80
50/50 [==============================] - 31s 627ms/step - loss: 0.0518 - acc: 0.9860 - val_loss: 6.9036 - val_acc: 0.5000
Epoch 24/80
50/50 [==============================] - 31s 621ms/step - loss: 0.0738 - acc: 0.9810 - val_loss: 6.6649 - val_acc: 0.3500
Epoch 25/80
50/50 [==============================] - 30s 606ms/step - loss: 0.0146 - acc: 0.9980 - val_loss: 7.7122 - val_acc: 0.5000
Epoch 26/80
50/50 [==============================] - 34s 672ms/step - loss: 0.0453 - acc: 0.9880 - val_loss: 7.4843 - val_acc: 0.4500
Epoch 27/80
50/50 [==============================] - 32s 639ms/step - loss: 0.0367 - acc: 0.9870 - val_loss: 7.6371 - val_acc: 0.5000
Epoch 28/80
50/50 [==============================] - 30s 597ms/step - loss: 0.0241 - acc: 0.9950 - val_loss: 8.1453 - val_acc: 0.5000
Epoch 29/80
50/50 [==============================] - 30s 592ms/step - loss: 0.0326 - acc: 0.9920 - val_loss: 8.2151 - val_acc: 0.4500
Epoch 30/80
50/50 [==============================] - 30s 606ms/step - loss: 0.0502 - acc: 0.9890 - val_loss: 8.4432 - val_acc: 0.5000
Epoch 31/80
50/50 [==============================] - 30s 597ms/step - loss: 0.0163 - acc: 0.9970 - val_loss: 8.0083 - val_acc: 0.5000
Epoch 32/80
50/50 [==============================] - 29s 582ms/step - loss: 0.0362 - acc: 0.9920 - val_loss: 7.9444 - val_acc: 0.5000
Epoch 33/80
50/50 [==============================] - 30s 609ms/step - loss: 0.0346 - acc: 0.9880 - val_loss: 8.3872 - val_acc: 0.5000
Epoch 34/80
50/50 [==============================] - 29s 584ms/step - loss: 0.0258 - acc: 0.9950 - val_loss: 8.8647 - val_acc: 0.5000
Epoch 35/80
50/50 [==============================] - 29s 588ms/step - loss: 0.0362 - acc: 0.9880 - val_loss: 8.4899 - val_acc: 0.5500
Epoch 36/80
50/50 [==============================] - 30s 595ms/step - loss: 0.0276 - acc: 0.9920 - val_loss: 8.2845 - val_acc: 0.5000
Epoch 37/80
50/50 [==============================] - 29s 582ms/step - loss: 0.0189 - acc: 0.9940 - val_loss: 8.6437 - val_acc: 0.5000
Epoch 38/80
50/50 [==============================] - 31s 611ms/step - loss: 0.0092 - acc: 0.9960 - val_loss: 8.5518 - val_acc: 0.4500
Epoch 39/80
50/50 [==============================] - 29s 586ms/step - loss: 0.0230 - acc: 0.9920 - val_loss: 8.7936 - val_acc: 0.3500
Epoch 40/80
50/50 [==============================] - 29s 580ms/step - loss: 0.0162 - acc: 0.9960 - val_loss: 9.2228 - val_acc: 0.4500
Epoch 41/80
50/50 [==============================] - 29s 582ms/step - loss: 0.0231 - acc: 0.9960 - val_loss: 9.2710 - val_acc: 0.4500
Epoch 42/80
50/50 [==============================] - 29s 586ms/step - loss: 0.0372 - acc: 0.9960 - val_loss: 10.0153 - val_acc: 0.5000
Epoch 43/80
50/50 [==============================] - 29s 586ms/step - loss: 0.0080 - acc: 0.9970 - val_loss: 11.3972 - val_acc: 0.5000
Epoch 44/80
50/50 [==============================] - 29s 583ms/step - loss: 0.0292 - acc: 0.9950 - val_loss: 10.8015 - val_acc: 0.3000
Epoch 45/80
50/50 [==============================] - 29s 578ms/step - loss: 0.0438 - acc: 0.9890 - val_loss: 10.0119 - val_acc: 0.4500
Epoch 46/80
50/50 [==============================] - 29s 579ms/step - loss: 0.0271 - acc: 0.9900 - val_loss: 10.0108 - val_acc: 0.5000
Epoch 47/80
50/50 [==============================] - 30s 597ms/step - loss: 0.0106 - acc: 0.9970 - val_loss: 10.5471 - val_acc: 0.5500
Epoch 48/80
50/50 [==============================] - 29s 590ms/step - loss: 0.0323 - acc: 0.9930 - val_loss: 9.5484 - val_acc: 0.3000
Epoch 49/80
50/50 [==============================] - 29s 583ms/step - loss: 0.0283 - acc: 0.9960 - val_loss: 10.2763 - val_acc: 0.5000
Epoch 50/80
50/50 [==============================] - 31s 619ms/step - loss: 0.0344 - acc: 0.9920 - val_loss: 9.9814 - val_acc: 0.4500
Epoch 51/80
50/50 [==============================] - 29s 572ms/step - loss: 0.0175 - acc: 0.9920 - val_loss: 9.7044 - val_acc: 0.5500
Epoch 52/80
50/50 [==============================] - 29s 577ms/step - loss: 0.0112 - acc: 0.9980 - val_loss: 11.7453 - val_acc: 0.5500
Epoch 53/80
50/50 [==============================] - 29s 588ms/step - loss: 0.0221 - acc: 0.9930 - val_loss: 10.2242 - val_acc: 0.4500
Epoch 54/80
50/50 [==============================] - 29s 574ms/step - loss: 0.0165 - acc: 0.9970 - val_loss: 10.1135 - val_acc: 0.5000
Epoch 55/80
50/50 [==============================] - 28s 565ms/step - loss: 0.0057 - acc: 0.9980 - val_loss: 10.6202 - val_acc: 0.4000
Epoch 56/80
50/50 [==============================] - 28s 566ms/step - loss: 0.0350 - acc: 0.9930 - val_loss: 11.1900 - val_acc: 0.5000
Epoch 57/80
50/50 [==============================] - 28s 567ms/step - loss: 0.0022 - acc: 1.0000 - val_loss: 11.1339 - val_acc: 0.4500
Epoch 58/80
50/50 [==============================] - 28s 566ms/step - loss: 0.0343 - acc: 0.9940 - val_loss: 11.2391 - val_acc: 0.4500
Epoch 59/80
50/50 [==============================] - 29s 571ms/step - loss: 0.0167 - acc: 0.9950 - val_loss: 11.1921 - val_acc: 0.5000
Epoch 60/80
50/50 [==============================] - 28s 568ms/step - loss: 0.0060 - acc: 0.9980 - val_loss: 11.5785 - val_acc: 0.4500
Epoch 61/80
50/50 [==============================] - 29s 578ms/step - loss: 0.0451 - acc: 0.9950 - val_loss: 11.7180 - val_acc: 0.5000
Epoch 62/80
50/50 [==============================] - 28s 567ms/step - loss: 0.0036 - acc: 0.9990 - val_loss: 14.4340 - val_acc: 0.5000
Epoch 63/80
50/50 [==============================] - 28s 566ms/step - loss: 0.0267 - acc: 0.9940 - val_loss: 11.9684 - val_acc: 0.4000
Epoch 64/80
50/50 [==============================] - 31s 622ms/step - loss: 0.0079 - acc: 0.9970 - val_loss: 11.3762 - val_acc: 0.4000
Epoch 65/80
50/50 [==============================] - 28s 557ms/step - loss: 0.0695 - acc: 0.9870 - val_loss: 12.1722 - val_acc: 0.4500
Epoch 66/80
50/50 [==============================] - 28s 568ms/step - loss: 0.0130 - acc: 0.9940 - val_loss: 12.1978 - val_acc: 0.4500
Epoch 67/80
50/50 [==============================] - 28s 565ms/step - loss: 0.0188 - acc: 0.9970 - val_loss: 11.7762 - val_acc: 0.4000
Epoch 68/80
50/50 [==============================] - 28s 557ms/step - loss: 0.0011 - acc: 1.0000 - val_loss: 13.2410 - val_acc: 0.4500
Epoch 69/80
50/50 [==============================] - 28s 564ms/step - loss: 0.0431 - acc: 0.9960 - val_loss: 12.7333 - val_acc: 0.4500
Epoch 70/80
50/50 [==============================] - 28s 562ms/step - loss: 0.0104 - acc: 0.9980 - val_loss: 13.0937 - val_acc: 0.5000
Epoch 71/80
50/50 [==============================] - 28s 561ms/step - loss: 0.0140 - acc: 0.9970 - val_loss: 12.4452 - val_acc: 0.3500
Epoch 72/80
50/50 [==============================] - 28s 553ms/step - loss: 0.0212 - acc: 0.9960 - val_loss: 12.7357 - val_acc: 0.4500
Epoch 73/80
50/50 [==============================] - 28s 562ms/step - loss: 0.0036 - acc: 0.9990 - val_loss: 13.4253 - val_acc: 0.5000
Epoch 74/80
50/50 [==============================] - 28s 561ms/step - loss: 0.0036 - acc: 0.9980 - val_loss: 12.7524 - val_acc: 0.4500
Epoch 75/80
50/50 [==============================] - 28s 561ms/step - loss: 0.0068 - acc: 0.9990 - val_loss: 12.5598 - val_acc: 0.4500
Epoch 76/80
50/50 [==============================] - 28s 556ms/step - loss: 0.0240 - acc: 0.9960 - val_loss: 13.6739 - val_acc: 0.5000
Epoch 77/80
50/50 [==============================] - 28s 555ms/step - loss: 0.0099 - acc: 0.9970 - val_loss: 13.9698 - val_acc: 0.5000
Epoch 78/80
50/50 [==============================] - 28s 550ms/step - loss: 0.0027 - acc: 1.0000 - val_loss: 13.4390 - val_acc: 0.4500
Epoch 79/80
50/50 [==============================] - 28s 555ms/step - loss: 0.0390 - acc: 0.9960 - val_loss: 13.6321 - val_acc: 0.4500
Epoch 80/80
50/50 [==============================] - 28s 559ms/step - loss: 0.0023 - acc: 0.9990 - val_loss: 13.6142 - val_acc: 0.4000

让我们保存我们的模型——我们将在convnet可视化部分中使用它。

model.save('cats_and_dogs_small_2.h5')

让我们再次绘制结果：

acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(len(acc))

plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()

plt.figure()

plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()

plt.show()

由于数据的增加和丢失，我们不再过度拟合：训练曲线非常接近于验证

曲线。我们现在能够达到82%的精度，比非正则模型相对提高了15%。

通过进一步利用正则化技术和调整网络参数（例如每个卷积的滤波器数量层，或者网络中的层数），我们可以得到更好的精度，可能高达86-87%。然而，这将证明仅仅通过从头开始训练我们自己的convnet就很难再上一层楼，因为我们要处理的数据太少了。作为一个下一步，为了提高我们在这个问题上的准确性，我们必须利用一个预先训练过的模型，这将是下两个问题的重点部分。