ArcFace 论文阅读及 pytorch 实现
ArcFace: Additive Angular Margin Loss for Deep Face Recognition
论文: https://arxiv.org/abs/1801.07698
官方代码: https://github.com/deepinsight/insightface
Abstract
大规模人脸识别的挑战之一就是如何设计损失函数,以增强判别能力。Centre loss: 惩罚人脸深层特征与其相应的类中心在欧氏空间中的距离,以缩小类内距离; SphereFace: 假设最后一个全连接层中的线性变换矩阵可以表示角度空间中类别中心,并以乘法的方式惩罚深特征与其相应权重之间的角度。目前的研究主线是在已有的损失函数中加入裕度,以增强对人脸的分类能力,本文提出 Additive Angular Margin Loss (ArcFace) 增强使用特征进行人脸分类的能力,将人脸识别的能力提高了10个点。
Introduction
当前,使用 DCNN (Deep Convolutional Neural Network) 进行人脸识别主要有两条研究路线,一种是使用 Softmax 直接训练一个分类器,对不同 ID 的人脸进行分类; 另一种是直接学习嵌入 (learn dirtectly an embedding)(个人理解:应该是基于对比识别的方式,例如 Siamese 和 Triplet),例如 Triplet Loss。但是 softmax loss 和 triplet loss 都有缺点,对于 softmax loss:
- 线性变换矩阵 W ∈ R d × n W \in R^{d\times n} W∈Rd×n 的维度随着 ID 数量 n n n 的增加而线性增加;
- 学习到的特征对于 closed-set 的分类效果很好,但是对于 open-set 的判别能力不够 (个人理解:对于不会增加其他类别的数据集,使用分类可以取得较好的结果,但是像是在人脸识别的使劲落地中,训练集中往往没有应用场景中的人物 ID,需要增加人物 ID,这是分类就无法解决);
对于 triplet loss:
- 在 ID 数量和数据量多的大规模数据集上,存在组合爆炸的问题,会导致迭代步数的急剧增加 (个人理解:Siamese 和 Triplet 这种通过对比进行人脸识别的网络,需要将数据集中的数据进行配对,当 ID 的数据量和数据量大时,配对组合形成大量的数据,造成组合爆炸,训练时需要更多的迭代步数);
- 半难样本挖掘 (semi-hard sample mining) 对模型性能的提高是一个难题 (个人理解:在通过对别识别时,需要对网络对配对图像的识别能力进行评估,将难以识别的组合进行加强训练,但是如何找出难以识别的组合,提高训练模型的性能是一个难题);
多种 softmax 的变体被提出,用于增强人脸识别的判别能力。Centre loss: 惩罚特征向量和类别中心在欧式空间中的距离来增强类内的紧密性,使用级联的 Softmax loss 来保证类间的分离性。但是,在训练时随着 ID 数量的增加,更新类别中心十分困难。SphereFace提出了角度裕度的概念,但是损失函数需要一系列近似才能计算出来,这会导致网络训练的不稳定。为了训练过程的稳定,提出看包含标准 softmax 的混合损失函数。由于基于整数的乘性角度裕度 (integer-based multiplicative angular margin) 使目标逻辑 (target logit) 曲线变得十分陡峭,会阻碍收敛,所以从经验中得出, softmax 控制训练过程。CosFace直接在目标逻辑中增加余弦裕度惩罚,得到了比 SphereFace更好的结果,并且实施起来更加简单,减少了对 softmax 的依赖。
Additive Angular Margin Loss (ArcFace)
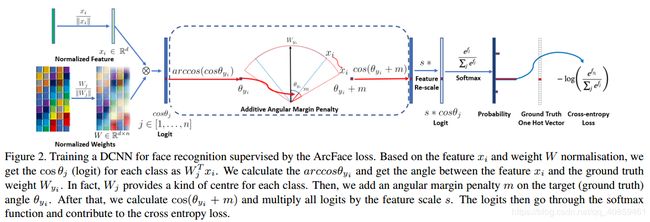
如上图所示,DCNN 的特征与最后一层全连接层的点积等于特征与权重归一化之后的余弦距离,1. ArcFace 先使用反余弦函数计算当前特征与目标权重之间的角度,然后在目标角度上增加附加角裕度,最后使用余弦函数重新得到目标 logits。2. 通过固定的特征归一化重新改变所有 logits 的大小,剩下的步骤与 softmax 完全相同。
ArcFace 有如下优点:
- Engaging
通过归一化超球面中角和弧的精确对应关系,直接优化距离裕度。通过分析特征和权重之间的角度统计,直观地说明 512-D 空间中的情况; - Effective
将 SOTA 提高了10 个点; - Easy
按照伪代码,仅需几行代码即可实现,不依赖其他损失函数即有较好的稳定性,在任何数据集上都很容易收敛;
- Efficient
在训练时仅增加少许计算复杂度,在 ID 多的数据集上也可以使用;
Proposed Approach
ArcFace
最常使用的分类损失函数是 softmax,即
L 1 = − 1 N ∑ i = 1 N l o g e W y i T x i + b y i ∑ j = 1 n e W j T x i + b j L_1=-\frac{1}{N}\sum_{i=1}^{N}log\frac{e^{W_{y_i}^{T}x_{i}+b_{y_i}}}{\sum_{j=1}^{n}e^{W_{j}^{T}x_i+b_j}} L1=−N1i=1∑Nlog∑j=1neWjTxi+bjeWyiTxi+byi
其中, x i ∈ R d x_i\in R^d xi∈Rd 表示第 i i i 个样本的特征,该样本属于第 y i y_i yi 类,文中的特征维度 d d d 设置为 512 512 512, W j ∈ R d W_j\in R^d Wj∈Rd 表示权重 W ∈ R d × n W\in R^{d\times n} W∈Rd×n 的第 j j j 列, b j ∈ R n b_j\in R^n bj∈Rn 是偏置项, N N N 是 batch size, n n n 是类别数量;
softmax 没有优化特征嵌入 (feature embeding) 以增强样本的类内相似性和类间的分离性,导致在人脸识别领域的表现不是很好。
为了简化,固定偏置 b j = 0 b_j=0 bj=0,
L 2 = − 1 N ∑ i = 1 N l o g e W y i T x i ∑ j = 1 n e W j T x i L_2=-\frac{1}{N}\sum_{i=1}^{N}log\frac{e^{W_{y_i}^{T}x_{i}}}{\sum_{j=1}^{n}e^{W_{j}^{T}x_i}} L2=−N1i=1∑Nlog∑j=1neWjTxieWyiTxi
点积变换 W j T x i = ∥ W j ∥ ∥ x i ∥ c o s θ j W_j^Tx_i=\left \| W_j \right \| \left \| x_i \right \|cos\theta_j WjTxi=∥Wj∥∥xi∥cosθj,
L 3 = − 1 N ∑ i = 1 N l o g e ∥ W y j ∥ ∥ x i ∥ c o s θ y i e ∥ W y j ∥ ∥ x i ∥ c o s θ y i + ∑ j = 1 , j ≠ y i n e ∥ W j ∥ ∥ x i ∥ c o s θ j L_3=-\frac{1}{N}\sum_{i=1}^{N}log\frac{e^{\left \| W_{y_j} \right \| \left \| x_i \right \|cos\theta_{y_i}}}{e^{\left \| W_{y_j} \right \| \left \| x_i \right \|cos\theta_{y_i}} + \sum_{j=1, j\neq y_i}^{n}e^{\left \| W_{j} \right \| \left \| x_i \right \|cos\theta_{j}}} L3=−N1i=1∑Nloge∥Wyj∥∥xi∥cosθyi+∑j=1,j̸=yine∥Wj∥∥xi∥cosθje∥Wyj∥∥xi∥cosθyi
其中 θ j \theta_j θj是权重 W j W_j Wj和特征 x i x_i xi之间的角度。在经过 l 2 l_2 l2 归一化后,固定权重 ∥ W j ∥ = 1 \left \| W_j \right \|=1 ∥Wj∥=1,固定 l 2 l_2 l2 归一化后的特征 ∥ x i ∥ \left \| x_i \right \| ∥xi∥ 为 s s s,则
L 4 = − 1 N ∑ i = 1 N l o g e s c o s θ y i e s c o s θ y i + ∑ j = 1 , j ≠ y i n e s c o s θ j L_4=-\frac{1}{N}\sum_{i=1}^{N}log\frac{e^{s\ cos\theta_{y_i}}}{e^{s\ cos\theta_{y_i}}+\sum_{j=1, j\neq y_i}^{n}e^{s\ cos\theta_j}} L4=−N1i=1∑Nloges cosθyi+∑j=1,j̸=yines cosθjes cosθyi
特征与权重归一化网络的预测只依赖于特征和权重之间的角度,学习到的特征以半径 s s s 分布在球体上:
当嵌入特征分布在超球面上每个特征的中心周围时,使用附加角度裕度 m m m惩罚特征 x i x_i xi 和权值 W y i W_{y_i} Wyi 之间的距离,增加类内的致密性和类间的分离性,即
L 5 = − 1 N ∑ i = 1 N l o g e s c o s ( θ y i + m ) e s c o s ( θ y i + m ) + ∑ j = 1 , j ≠ y i n e s c o s θ j L_5=-\frac{1}{N}\sum_{i=1}^{N}log\frac{e^{s\ cos(\theta_{y_{i}}+m)}}{e^{s\ cos(\theta_{y_i}+m)}+\sum_{j=1, j\neq y_i}^{n}e^{s\ cos\theta_j}} L5=−N1i=1∑Nloges cos(θyi+m)+∑j=1,j̸=yines cosθjes cos(θyi+m)
由于提出的附加角度裕度惩罚相当于在归一化后超球面的距离裕度惩罚,所以该方法被成为 ArcFace:

选用 8 个不同 ID 的人脸图像,每个 ID 的样本大约有 1500 张图像的数据集分别使用 softmax 和 ArcFace 进行训练,如上图所示,softmax 训练出的特征仅能提供模糊的决策边界,而 ArcFace 可以显著拉大相近类别之间的距离。
Comparison with SphereFace and CosFace
-
Numerical Similarity 数值相似性
SphereFace、ArcFace 和 CosFace 分别提出了不同的裕度惩罚,分别为乘性角度裕度 m 1 m_1 m1,附加角度裕度 m 2 m_2 m2 和附加余弦裕度 m 3 m_3 m3。从数值角度看,所有的裕度惩罚都是通过惩罚目标 logit ,以增加类内的致密性和类间的分离性。在图4(b)中绘出了三者在最佳裕度下的目标逻辑曲线,由于 W y W_y Wy和 x i x_i xi之间的角度是从 9 0 ∘ 90^\circ 90∘ 开始 (随机初始化),到 3 0 ∘ 30^\circ 30∘结束,所以仅展示了在 [ 2 0 ∘ , 10 0 ∘ ] [20^\circ, 100^\circ] [20∘,100∘] 角度范围内的目标 logit 曲线。作者猜测目标 logit 曲线上有三个因素影响性能,即起始点、终止点和斜率。
级联所有的裕度惩罚,在同一框架下同时使用 SphereFace、ArcFace 和 CosFace, m 1 , m 2 , m 3 m_1, m_2, m_3 m1,m2,m3 均为超参数:
L 6 = − 1 N ∑ i = 1 N l o g e s ( c o s ( m 1 θ y i + m 2 ) − m 3 ) e s ( c o s ( m 1 θ y i + m 2 ) − m 3 ) + ∑ j = 1 , j ≠ y i n e s c o s θ j L_6=-\frac{1}{N}\sum_{i=1}^{N}log\frac{e^{s(cos(m_1\theta_{y_{i}}+m_2)-m_3)}}{e^{s(cos(m_1\theta_{y_i}+m_2)-m_3)}+\sum_{j=1, j\neq y_i}^{n}e^{s\ cos\theta_j}} L6=−N1i=1∑Nloges(cos(m1θyi+m2)−m3)+∑j=1,j̸=yines cosθjes(cos(m1θyi+m2)−m3)
-
Geometric Difference 几何差异
ArcFace 有更好的几何属性,如下图所示,ArcFace 有恒定的角裕度,而 CosFace 和 SphereFace 仅有非线性的角裕度。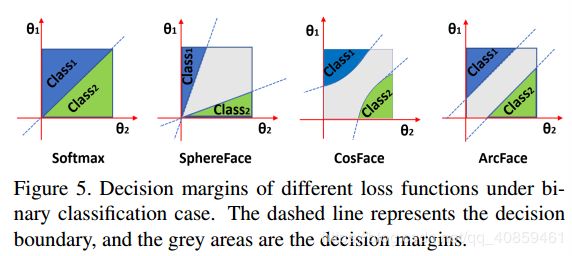
裕度设计的微小差异就有可能在模型训练过程中产生蝴蝶效应。例如,SphereFace 使用退火处理的优化策略,为了避免训练开始时的发散,使用 Softmax 进行监督,削弱乘性裕度的惩罚。在 ArcFace 中,使用在裕度中无需整数的新版本 SphereFace,采用反余弦函数代替复杂的双倍角度公式,当 m = 1.35 m=1.35 m=1.35 时可以获得与原版的 SphereFace 相似的性能,并且没有任何收敛困难。
Comparison with Other Losses

- Intra-Loss
通过减小样本和 groundtruth 之间的角度/弧度,提高类内的致密性:
L 5 = L 2 + 1 π N ∑ i = 1 N θ y i L_5=L_2+\frac{1}{\pi N}\sum_{i=1}^{N}\theta_{y_i} L5=L2+πN1i=1∑Nθyi - Inter-Loss
通过增大不同中心之间的角度/弧度,以增强类间的分离性:
L 6 = L 2 − 1 π N ( n − 1 ) ∑ i = 1 N ∑ j = 1 , j ≠ y i n a r c c o s ( W y i T W j ) L_6=L_2-\frac{1}{\pi N(n-1)}\sum_{i=1}^{N}\sum_{j=1,j\neq y_i}^{n}arccos(W_{y_i}^{T}W_j) L6=L2−πN(n−1)1i=1∑Nj=1,j̸=yi∑narccos(WyiTWj)
Inter-Loss 是 Minimum Hyper-spherical Energy (MHE) 的一种特殊情况,在 MHE 中,隐藏层和输出层都被正则化; - Triplet-Loss
扩大三个样本之间的角度/弧度裕度;
a r c c o s ( x i p o s x i ) + m ≤ a r c c o s ( x i n e g x i ) arccos(x_i^{pos}x_i)+m\leq arccos(x_i^{neg}x_i) arccos(xiposxi)+m≤arccos(xinegxi)
代码实现
- pytorch
from __future__ import print_function from __future__ import division import torch import torch.nn as nn import torch.nn.functional as F from torch.nn import Parameter import math class ArcMarginProduct(nn.Module): r"""Implement of large margin arc distance: : Args: in_features: size of each input sample out_features: size of each output sample s: norm of input feature m: margin cos(theta + m) """ def __init__(self, in_features, out_features, s=30.0, m=0.50, easy_margin=False): super(ArcMarginProduct, self).__init__() self.in_features = in_features self.out_features = out_features self.s = s self.m = m self.weight = Parameter(torch.FloatTensor(out_features, in_features)) nn.init.xavier_uniform_(self.weight) self.easy_margin = easy_margin self.cos_m = math.cos(m) self.sin_m = math.sin(m) self.th = math.cos(math.pi - m) self.mm = math.sin(math.pi - m) * m def forward(self, input, label): # --------------------------- cos(theta) & phi(theta) --------------------------- cosine = F.linear(F.normalize(input), F.normalize(self.weight)) sine = torch.sqrt(1.0 - torch.pow(cosine, 2)) phi = cosine * self.cos_m - sine * self.sin_m if self.easy_margin: phi = torch.where(cosine > 0, phi, cosine) else: phi = torch.where(cosine > self.th, phi, cosine - self.mm) # --------------------------- convert label to one-hot --------------------------- # one_hot = torch.zeros(cosine.size(), requires_grad=True, device='cuda') one_hot = torch.zeros(cosine.size(), device='cuda') one_hot.scatter_(1, label.view(-1, 1).long(), 1) # -------------torch.where(out_i = {x_i if condition_i else y_i) ------------- output = (one_hot * phi) + ((1.0 - one_hot) * cosine) # you can use torch.where if your torch.__version__ is 0.4 output *= self.s # print(output) return output