牛顿法与梯度下降法的讲解与Python代码实现
牛顿法与梯度下降法的讲解与Python代码实现
- 一、牛顿法概述
- 基本牛顿法原理
- Python实现牛顿法
- 二、梯度下降法概述
- 梯度下降算法
- 2.1场景假设
- 2.2梯度下降法过程
- Python代码实现梯度下降法
一、牛顿法概述
高斯-牛顿法是另一种经常用于求解非线性最小二乘的迭代法(一定程度上可视为标准非线性最小二乘求解方法)。
牛顿法也是机器学习中用的比较多的一种优化算法。牛顿法的基本思想是利用迭代点![]() 处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值。牛顿法的速度相当快,而且能高度逼近最优值。牛顿法分为基本的牛顿法和全局牛顿法。下面我将介绍基本牛顿法。
处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值。牛顿法的速度相当快,而且能高度逼近最优值。牛顿法分为基本的牛顿法和全局牛顿法。下面我将介绍基本牛顿法。
基本牛顿法原理
基本牛顿法是一种是用导数的算法,它每一步的迭代方向都是沿着当前点函数值下降的方向。
我们主要集中讨论在一维的情形,对于一个需要求解的优化函数![]() ,求函数的极值的问题可以转化为求导函数。对函数进行泰勒展开到二阶,得到
,求函数的极值的问题可以转化为求导函数。对函数进行泰勒展开到二阶,得到
![]()
对上式求导并令其为0,则为
![]()
即得到
![]()
牛顿法具有二次收敛性,因此比普通的梯度下降收敛的更快。
虽然牛顿法的收敛速度很快,但是有比较多的限制,比如函数必须具有二阶偏导,黑塞矩阵必须正定。牛顿法需要计算黑塞矩阵及其逆,需要进行大量的运算,计算相当复杂。克服这些问题的方法就是拟牛顿法。关于拟牛顿法我们以后再叙。
Python实现牛顿法
import numpy as np
import matplotlib.pyplot as plt
# input
'''
x0:初始值
theta:阈值
'''
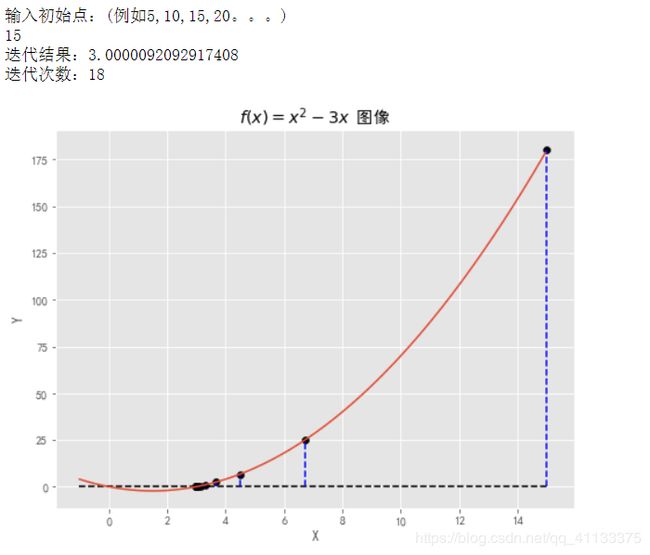
x0=float(input('输入初始点:(例如5,10,15,20。。。)\n'))
theta=1e-5
#可以显示中文
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams['axes.unicode_minus'] = False
# 设置风格
plt.style.use('ggplot')
# 定义函数,构造数值
init_fun = lambda x: x**2-3*x
tran_fun = lambda x: np.sqrt(3*x)
# 函数图像
fig_1 = plt.figure(figsize = (8, 6))
plt.xlabel('X')
plt.ylabel('Y')
plt.title('$f(x)=x^2-3x$ 图像')
# 函数图像
x=[]
if x0>0:
x = np.arange(-1,x0,0.05)
plt.hlines(0,-1,x0,'black','--')
else:
x = np.arange(x0,10,0.05)
plt.hlines(0,x0,10,'black','--')
y = init_fun(x)
# 迭代法
def iterative(func = tran_fun, x0 = x0,theta = theta):
number=0
xi = x0
while True and number <= 100:
xi = func(x0)
plt.vlines(x0,0,init_fun(x0),'blue','--')
plt.scatter(x0,init_fun(x0),c='black')
if abs(xi-x0) < theta:
return xi,number
x0 = xi
number += 1
# 迭代法计算求解x0
xi,number = iterative(tran_fun, x0, theta)
print('迭代结果:'+str(xi))
print('迭代次数:'+str(number))
## 函数求解
plt.plot(x,y)
plt.show()
二、梯度下降法概述
梯度下降(gradient descent)在机器学习中应用十分的广泛,不论是在线性回归还是Logistic回归中,它的主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值。
梯度下降算法
2.1场景假设
梯度下降法的基本思想可以类比为一个下山的过程。
假设这样一个场景:一个人被困在山上,需要从山上下来(找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低;因此,下山的路径就无法确定,必须利用自己周围的信息一步一步地找到下山的路。这个时候,便可利用梯度下降算法来帮助自己下山。怎么做呢,首先以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着下降方向走一步,然后又继续以当前位置为基准,再找最陡峭的地方,再走直到最后到达最低处;同理上山也是如此,只是这时候就变成梯度上升算法了。
2.2梯度下降法过程
我们以一个人下山为例。比如刚开始的初始位置是在山顶位置,那么现在的问题是该如何达到山底呢?按照梯度下降算法的思想,它将按如下操作达到最低点:
第一步,明确自己现在所处的位置
第二步,找到相对于该位置而言下降最快的方向
第三步, 沿着第二步找到的方向走一小步,到达一个新的位置,此时的位置肯定比原来低
第四部, 回到第一步
第五步,终止于最低点
按照以上5步,最终达到最低点,这就是梯度下降的完整流程。当然这是针对标准的凸函数而言的,如果不是标准的凸函数,我们就需要找不同的初始位置进行梯度下降了。
其优点是工作量少,存储变量较少,初始点要求不高;
缺点是收敛慢,效率不高, 有时达不到最优解。
Python代码实现梯度下降法
函数y=x * x+2 * y * y-4 * x-2 * x * y
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
def Fun(x,y):#原函数
return x*x+2*y*y-4*x-2*x*y
def PxFun(x,y):#偏x导
return 2*x-4-2*y
def PyFun(x,y):#偏y导
return 4*y-2*x
#初始化
fig=plt.figure()#figure对象
ax=Axes3D(fig)#Axes3D对象
X,Y=np.mgrid[-2:2:40j,-2:2:40j]#取样并作满射联合
Z=Fun(X,Y)#取样点Z坐标打表
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap="rainbow")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
#梯度下降
step=0.0008#下降系数
x=1
y=1#初始选取一个点
tag_x=[x]
tag_y=[y]
iter_num = 0#迭代次数
tag_z=[Fun(x,y)]#三个坐标分别打入表中,该表用于绘制点
new_x=x
new_y=y
Over=False
while Over==False:
new_x-=step*PxFun(x,y)
new_y-=step*PyFun(x,y)#分别作梯度下降
if Fun(x,y)-Fun(new_x,new_y)<7e-9:#精度
Over=True
x=new_x
y=new_y#更新旧点
tag_x.append(x)
tag_y.append(y)
tag_z.append(Fun(x,y))#新点三个坐标打入表中
iter_num += 1
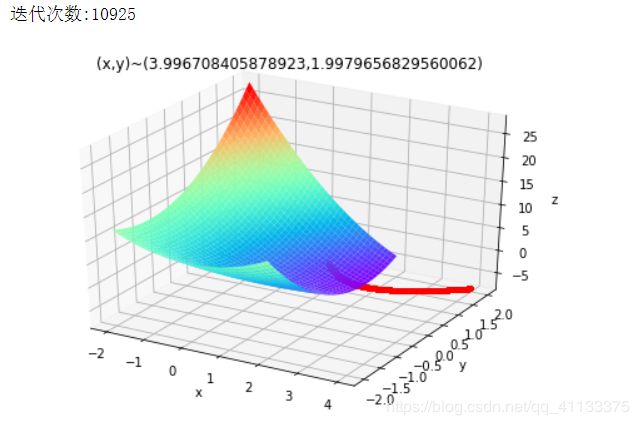
print(u"迭代次数:%d" % iter_num)
#绘制点/输出坐标
ax.plot(tag_x,tag_y,tag_z,'r.')
plt.title('(x,y)~('+str(x)+","+str(y)+')')
plt.show()
- https://blog.csdn.net/ivysister/article/details/45438413?depth_1-utm_source=distribute.pc_relevant.none-task-blog-OPENSEARCH-1&utm_source=distribute.pc_relevant.none-task-blog-OPENSEARCH-1
- https://baijiahao.baidu.com/s?id=1639202882632470513&wfr=spider&for=pc
- https://blog.csdn.net/qq_41800366/article/details/86583789?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1