剑指offer刷题笔记
目录
- 一、数组中重复的数字
- 二、二维数组的查找
- 三、空格的替换
- 四、从尾到头打印单链表(不修改链表结构)
- 五、二叉树的重构
- 六、旋转数组的最小值
- 七、字符串转整数
一、数组中重复的数字
在一个长度为n的数组里的所有数字都在0到n-1的范围内。数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。
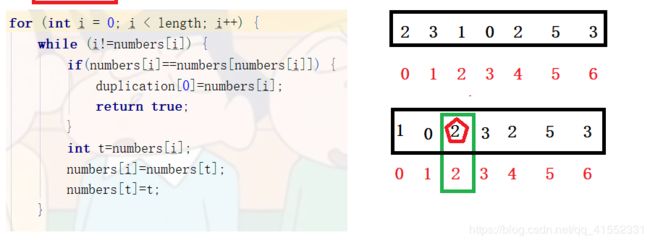
例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2
分析:
- 解法一:时间复杂度O(n),空间复杂度O(n)
由于所有元素值是有范围的,因此可以用一个长度为length的数组,下标表示序列中的每一个值,下标对应的值表示该下标出现的次数。
* 只需扫描一次原序列,就统计出所有元素出现的次数;
* 再扫描一次哈希数组,找到一个出现次数大于1的值即可。
public static boolean duplicate(int numbers[],int length,int [] duplication) {
if(numbers==null) {
return false;
}
// 判断数组是否合法(每个数都在0~n-1之间)
for ( int i=0; i<length; i++ ) {
if ( numbers[i]<0 || numbers[i]>length-1 ) {
return false;
}
}
int[] count=new int[length];//计数数组,就统计出所有元素出现的次数
for (int i = 0; i < numbers.length; i++) {
count[numbers[i]]++;
}
for (int i = 0; i < count.length; i++) {
if(count[i]>1) {
duplication[0]=i;
return true;
}
}
return false;
}
- 解法二:
*数组里的数在一定的范围内0~n-1,如果数据不重复的话,排序后每个数应该在其对应的下标内。
* 如果有重复的数字,说明有些位置可能存在多个数,有些位置没有数。
* 从头扫到尾,只要当前元素值与下标不同,就做一次断,numbers[i]与numbers[numbers[i]],相等就认为找到了重复元素,返回true,
* 否则就交换两者,继续循环。直到最后还没找到认为没找到重复元素,返回false
*
public static boolean duplicate1(int numbers[],int length,int [] duplication) {
if (numbers == null) {
return false;
}
// 判断数组是否合法(每个数都在0~n-1之间)
for (int i = 0; i < length; i++) {
if (numbers[i] < 0 || numbers[i] > length - 1) {
return false;
}
}
for (int i = 0; i < length; i++) {
while (i!=numbers[i]) {
if(numbers[i]==numbers[numbers[i]]) {
duplication[0]=numbers[i];
return true;
}
int t=numbers[i];
numbers[i]=numbers[t];
numbers[t]=t;
}
}
return false;
}
二、二维数组的查找
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数, 判断数组中是否含有该整数。
public boolean ind(int target, int [][] array) {
int i=array.length-1;
int j=0;
while (i>=0&&j<array[0].length) {
int k=array[i][j];
if(target>k){
j++;
}else if (target<k){
i--;
}else {
return true;
}
}
return false;
}
三、空格的替换
请实现一个函数,将一个字符串中的每个空格替换成“%20”。
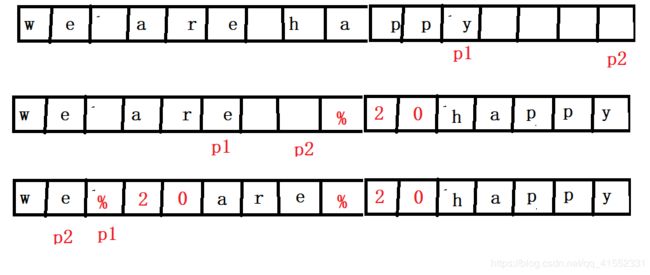
例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
- 首先我们遍历一次字符串获取字符串中空格的数量count。一个空格被替换成%20,替换完毕后,字符串的长度增加了count*2;
- 所以我们不妨建立一个长度为count*2+str.lenth的辅助数组,定义两个引用,如上图,一个指向新建数组的末尾。一个指向原数组的末尾。两个同时往前走,直至p1遇到第一个空格后,把p1向后移动一个位置。并在p2之前插入%20,并再把p2向前移动插入字符串的长度,如果p1没遇到空格将其位置的数放到p2位置,
public static String replaceSpace(StringBuffer str) {
if (str==null) {
throw new RuntimeException("字符串为null");
}
int count=0;//空格的个数
int len=str.toString().length();
for (int i = 0; i < len; i++) {
if(str.charAt(i)==' ') {
count++;
}
}
char[] arr=new char[len+count*2];
for (int i = 0; i < len; i++) {
arr[i]=str.charAt(i);
}
int p1=len-1;//指向原字符串的末尾
int p2=arr.length-1;//指向新数组的末尾
while(p1>=0&&p2>p1) {
if(arr[p1]!=' ') {
arr[p2--]=arr[p1];//将p1的字符往后搬移,知道遇见第一个空格
}else {
arr[p2--]='0';
arr[p2--]='2';
arr[p2--]='%';
}
p1--;
}
return new String(arr);
}
解法二,用StringBuffer自带api
public static String replaceSpace(StringBuffer str) {
if (str == null) {
return null;
} else {
StringBuffer newstr = new StringBuffer();
for (int i = 0; i < str.length(); i++) {
if (str.charAt(i) == ' ') {
newstr.append('%');
newstr.append('2');
newstr.append('0');
} else {
newstr.append(str.charAt(i));
}
}
return newstr.toString();
}
**启发:**当我们涉及到合并两个数组包括字符串时,如果,从前往后复制需要重复移动数字多次,我们可以考虑从后往前复制(减少移动次数),从而提高效率。例如下面这个例题
合并两个有序数组
四、从尾到头打印单链表(不修改链表结构)
思路:
方法一:就是利用栈先入后出的特性完成
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ArrayList<Integer> list = new ArrayList<>();
Stack<Integer> s=new Stack<>();
ListNode cur=listNode;
while(listNode!=null) {
s.push(listNode.val);
listNode=listNode.next;
}
while (!s.isEmpty()) {
list.add(s.pop());
}
return list;
}
方法二:递归
我们每打印一个节点时,先递归输出他后面的节点,在输出该节点本身。
ArrayList<Integer> arrayList=new ArrayList<Integer>();
public ArrayList<Integer> printListFromTailToHead1(ListNode listNode) {
if(listNode!=null){
printListFromTailToHead1(listNode.next);
arrayList.add(listNode.val);
}
return arrayList;
}
五、二叉树的重构
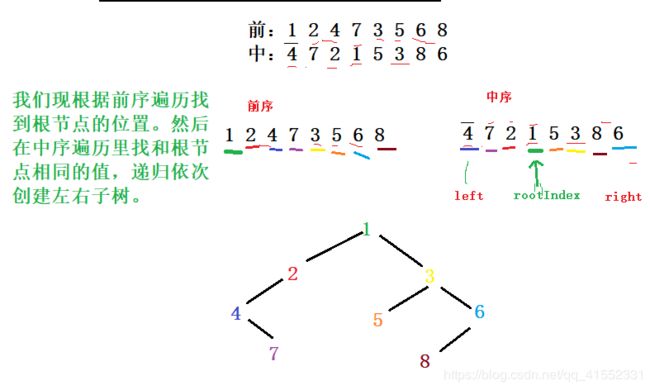
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
public class 重建二叉树 {
int index=0;//前序遍历根节点的下标
public TreeNode reConstructBinaryTree(int [] pre,int [] in,int left,int right) {
if(left>=right||index>=pre.length) {
return null;
}
TreeNode root=new TreeNode(pre[index]);//构建根
int rootIndex=left;//中序遍历根节点的下标
//在中序遍历里找到根
while(rootIndex<right) {
if(in[rootIndex]==pre[index]) {
break;
}
rootIndex++;
}
//根据该下标在中序遍历里依次构建左子树
++index;//找到根后,前序跟的下标后移,
//递归创建左子树
root.left=reConstructBinaryTree(pre,in,left,rootIndex);
//递归创建右子树
root.right=reConstructBinaryTree(pre,in,rootIndex+1,right);
return root;
}
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
return reConstructBinaryTree(pre,in,0,in.length);
}
}
六、旋转数组的最小值
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
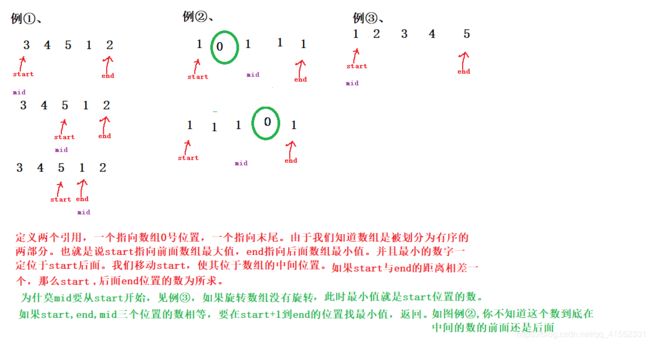
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
public class Solution {
public int minNumberInRotateArray(int [] array) {
int start=0;
int end=array.length-1;
int mid=start;
while(array[start]>=array[end]) {
if(end-start==1) {
mid=end;
break;
}
mid=(start+end)>>1;
if(array[start]==array[end]&&array[start]==array[mid]) {
//在start+1 到end里找最小值
int r=array[start];
for (int i = start+1; i <= end; i++) {
if(r>array[i]) {
r=array[i];
}
}
return r;
}
if(array[mid]>=array[start]) {
start=mid;
}else if(array[mid]<=array[end]){
end=mid;
}
}
return array[mid];
}
}
七、字符串转整数
public static int StrToInt(String str) {
if(str==null||str.equals("")) {
return 0;
}
int flag=0;
boolean t=false;
char[] nums=str.toCharArray();
int sum=0;
if(nums[0]=='-') {
flag = 1;
t=true;
}
if(nums[0]=='+') {
flag = 1;
}
for(int i=flag;i<nums.length;i++) {
if(nums[i]<'0'||nums[i]>'9') {
return 0;
}
sum=sum*10+nums[i]-'0';
}
return t ?-sum:sum;
}