吴恩达神经网络和深度学习-学习笔记-7-正则化regularization方法

解决高方差high variance的方法有两种：

• 正则化
• 准备更多数据

其中常用的正则化分为：

• L2正则化
• dropout正则化

L2正则化

L2正则化的原理

对于正则化的解释可以看一下这个博客【通俗易懂】机器学习中 L1 和 L2 正则化的直观解释

机器学习中，如果参数过多，模型过于复杂，容易造成过拟合（overfit）。即模型在训练样本数据上表现的很好，但在实际测试样本上表现的较差，不具备良好的泛化能力。为了避免过拟合，最常用的一种方法是使用使用正则化。

正则化的作用会让参数不会过大，避免发生过拟合的风险。具体每个参数的值还是通过梯度下降优化得到。

正则化一般选用L2正则化，L2正则化有时候也被叫为“权重衰减weight decay”
L2正则化公式：


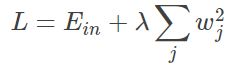
λ是一个需要调整的超参数。
正则项说明，不管w^[l]是什么，我们都试图让它变得更小。实际上相当于我们给矩阵W乘上了(1-αλ/m)倍的权重。
而该系数小于1，因此L2正则化也被成为“权重衰减”

L2正则化对不同权重的衰减是不同的，它取决于倍增的激活函数的大小（？？？）。

L2正则化避免过拟合overfitting（高方差high variance）

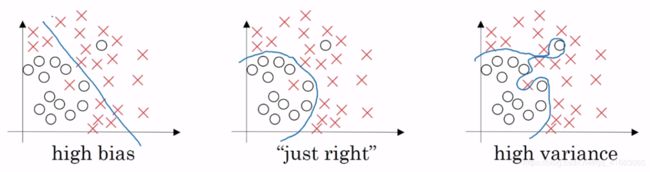
当λ很大的时候，w^[l]会约等于0，相当于一些隐藏单元不再起作用。这样一个复杂的神经网络就会得到化简（如下图所示）。

这样就会从左图所示的high variance(overfitting)向右图所示的high bias(underfitting)的方向发展（越来越接近逻辑回归 logistic regression），即减小variance。
但是λ会存在一个中间值，于是会有一个接近just right的中间状态。

最后我们借用tanh来直观感受下为什么正则化可以预防过拟合

当|z|较小时可以近似将激活函数tanh看作线性，当|z|较大时tanh为非线性。当λ较大时，w会较小，相应的使得z较小（z^[l] = w^[l] * A^[l-1] + b^[l]），从而对应到tanh的线性部分。这样每一层都可以近似视为线性。
而如果每层都是线性的，那么整个网络就是一个线性网络。这样的网络即使深度很大，由于其具有线性激活函数的特征，最终也只能计算线性函数。

dropout正则化（随机失活）

dropout的原理

dropout会遍历网络的每一层，并设置消除神经网络中节点的概率。
对于如下的神经网络，假设以0.5的概率dropout，则会有这样的结果：


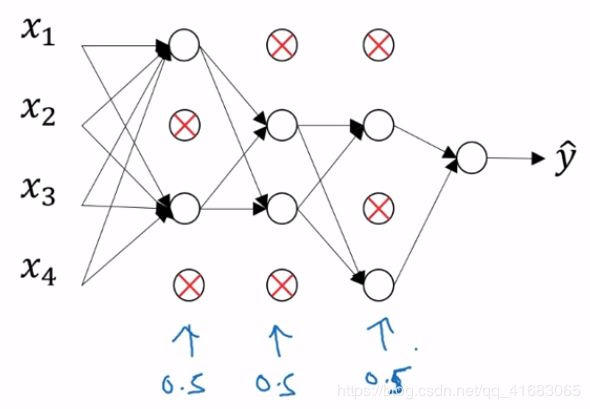
即得到一个节点更少，规模更小的网络（实现对网络的精简）。

再往深里将，对于单个的神经元，can’t rely on any one feature, so have to spread out weights（我觉得这句话总结的十分到位）

这样dropout将产生收缩权重的平方范数效果。和前面的L2正则化类似，dropout的结果是它会压缩权重（shrinks the weight），并完成一些预防过拟合的外层正则化。

事实证明，dropout可以被正式地作为一种正则化的替代形式。

dropout的实现

反向随机失活（invert dropout）
（我觉得直接调用PyTorch的dropout()函数即可

不同层的保存概率keep prob也可以不同，对于可能出现过拟合（含有诸多参数）的层可以低一点，对于不太可能出现过拟合的层可以高一点。

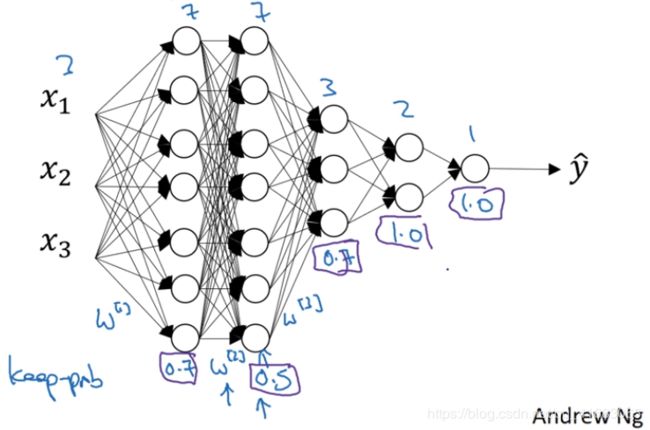
另外切记，dropout是用来解决过拟合问题的。也就是说当不会出现过拟合的问题时，我们便不会使用dropout。

对dropout的使用主要再计算机视觉领域，因为我们通常没有组构的数据，所以一直存在过拟合。

dropout的一大缺点就是代价函数J不再被明确定义，因为过程是随机的，所以很难完全复现。

吴恩达老师说：“我通常会关闭dropout函数，将keep prob的值设为1，运行代码，确保函数J单调递减。然后再打开dropout函数，再dropout的过程中代码并未引入bug。”

其他正则化方法

假训练数据

吴恩达老师介绍了一种成本几乎为0的数据扩充方法。

对原有图片进行反转裁剪旋转等操作。但是需要注意的是，这样得到的训练集有冗余，并不如我们收集一组新图片效果好。
以这种方式扩增算法数据，进而正则化数据集来减少过拟合比较廉价。
像这种人工合成数据的话，我们要通过算法验证图片中的猫经过水平翻转后依旧是猫。

early stopping

同时绘制训练集和验证集的损失函数

在开始训练的时候W很小（初始化为一个很小的随机量），在迭代和训练过程中W的值会变得却来越大。
所以early stopping要做的就是在中间点停止迭代，从而得到一个W值中等大小的弗罗贝尼乌斯范数（？？？）

吴恩达老师也讲到了early stopping的一个缺点：
他认为机器学习包括几个步骤：

• 选择一个算法来说优化代价函数J
  • 梯度下降
  • Momentum
  • RMSprop
  • Adam
  • ……
• 避免过拟合
  • 正则化
  • 扩增数据
  • ……

在机器学习中，超级参数激增，选出可行的算法也变得越来越复杂。
吴恩达老师发现，如果我们用一组工具优化代价函数J，机器学习就会变得更简单。在重点优化代价函数J时，只需要留意w和b，J(w, b)的值越小越好，你只需要想办法减小这个值，其他的不用关注。
然后，预防过拟合还有其他任务，换句话说就是减小方差，这一步我们用另外一套工具来实现。
这个原理有时被成为“正交化”，思路就是在一个时间做一个任务。

对吴恩达老师来说，early stopping的主要缺点是：你不能独立地处理这两个问题。
因为提早停止梯度下降，也就是停止了优化代价函数J（因为现在你不再尝试降低代价函数J），同时你又不希望出现过拟合，你没有采用两个不同的方式来解决这两个问题，而是用一种方法同时解决两个问题（我的理解是：你仅仅使用early stopping这一个方式来解决“优化代价函数J”和“预防过拟合”这两个问题）。
这样做的结果是，我要考虑的事情变得很复杂。如果不用early stopping，另一种方法就是L2正则化，then you can just train the neural networks as long as possible。我发现，这导致超参数搜索空间更容易分解，也更容易搜索（the search space of hyper parameters easier to decompose, and easier to search over）。但缺点在于，你必须尝试很多正则化参数λ的值，这也导致搜索大量的λ值的计算代价太高。
early stopping的优点是只运行一次梯度下降，你可以找出W的较小值、中间值和较大值，而无需尝试L2正则化超参数λ的很多值。
虽然L2正则化有缺点，但还是有很多人愿意用它。我（吴恩达老师）个人更倾向于使用L2正则化，尝试许多不同的λ值（这基于你可以负担大量计算的代价）。而使用early stopping也能得到相似结果，还不用尝试这么λ值。