Fourier,Laplace 和Z变换之间的关系探究

如果下面图挂了，请转https://www.bilibili.com/read/cv314506

本人是学工科的，并且没有开信号与系统和复变函数学的一塌糊涂的基础下，学控制系统设计和计算机控制，接触到了傅立叶变换和Z变换，拉普拉斯变换最早在大一学电路的时候用到，但是其实过了两年并不知道拉普拉斯变换在干嘛，最近也是觉得有必要去研究一下。我认为正因为是学工科的，我们才要理解性记忆，而不是死记硬背，我们要有自己的理解，这种理解并不需要牵扯到很深的数学，只要直观，形象，我们自己可以接受就是好的理解。我这里不会解释傅立叶和拉普拉斯变换的定义，只是要说它们之间的关系。

傅立叶积分是基础，它要做的就是将一个函数分解成一系列频率的三角函数的和，当然一般我们用欧拉公式把三角函数化为更紧凑的e指数形式

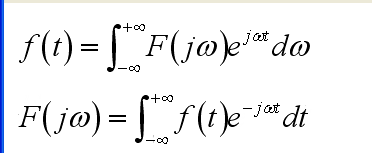
F(jw)被称为傅立叶变换，它表现为从时域转到频域，它描述的是一系列e指数的系数，可以说是包含一定频率三角函数用辅助角公式以后的幅值和相角的信息的一个函数。傅立叶逆变换是从频域到时域，其实就是

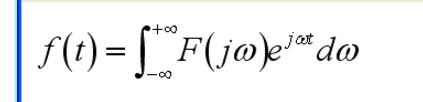
这个式子就是傅立叶逆变换，前面少打了个系数1/(2π），但是积分太麻烦，所以我们记住了一些对应法则对吧，阶跃函数啊，冲激函数啊，常数函数啊，余弦函数啊，这里我要提醒一点，狄利克雷条件只是充分条件，而不是必要条件，其中有一个条件叫做绝对可积。

其实这个说的是常数项对吧，你们应该都清楚，从积分里的绝对值你们应该可以理解为什么只是充分条件。也就是说不满足狄利克雷条件不一定不能傅立叶变换，只是需要用一些技巧，至于用了什么技巧，我相信来看的人应该至少学过信号与系统，书上都写有技巧，还有对于冲激函数这种广义函数怎么求都有，我写这篇文章不是为了讲这些，而是要讲三个变换之间的关系。但是有一些函数是真的没办法进行傅立叶变换，虽然我们不知道傅立叶变换的充要条件，但是我们可以理解，傅立叶变换是讲等幅震荡的余弦函数叠加，什么叫等幅震荡，不是说所有频率的余弦函数的赋值相等，而是说如果频率固定，这个频率的余弦函数随着时间的进行，赋值不变。那么就有一个问题，如果有信号随着时间趋于无穷函数值很大，比如e^a,a>0这种，用等幅震荡的余弦叠加是不可能去合成一个这样的信号，从常数项其实就能看到对吧，

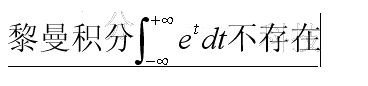
，于是就产生了拉普拉斯变换，拉普拉斯对傅立叶变换做了哪些改进呢？就是加入了一个衰减因子

用它去把原来升的太猛的函数给拉下来，让它黎曼可积，也就是说

如果知道了这点，你就会理解为什么拉普拉斯变换有一个条件是

这就是拉普拉斯变换对傅立叶变换的改进，这种改进其实们也可以人认为是用一种幅值随着时间不断增加的余弦函数去合成f(t)。

e^st是一系列赋值随时间指数上升的余弦函数。其实很容易理解。

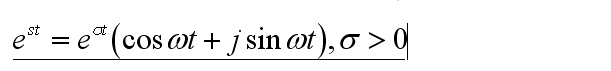
拉普拉斯逆变换呢？

就是这么个东西，前面少打了一个1/(2πj)，但是积分难算，所以我们又建立了一系列对应关系，然后让我们去记那个表或者说用部分分式法，留数法。接下来我们来说书上都说令s=jw,就把拉普拉斯变换变成了傅立叶变换，但是我们要注意一个东西，拉普拉斯变换存在对于s是有限制区域的，其实是对Res的限制，因为这个函数可能上升的太厉害，你需要很大的负指数才能把它拉下来，也就是我们说的收敛域。举个例子来说

就拿上面来说

说Z变换之前，我们先来说一个也是从傅立叶变换里过来的一个东西，叫小波变换（Wavelet transform），为什么会有小波变换呢？因为傅立叶变换损失了时域的信息，你不知道某个时间点的信号频率的信息，解决这个问题我们有两种办法，一个是用窗函数，还有一个就是小波变换。时域和频域的信息完整度是矛盾的，有点像测不准原理，事实上，在量子力学，测不准原理还就是这样。

然后我们就看看Z变换，Z变换是为了干嘛呢？其实Z变换就是拉普拉斯变换里做了一个小的技巧而已。

由于计算机技术的发展，工程领域现在广泛应用计算机。而计算机是二进制，所以说我们需要把时间和幅值上都连续的信号，也就是模拟信号转换为离散信号。所以说就需要采样，其实Z变换本质还是拉普拉斯变换，只是我们处理的不是模拟信号，而是在kT,k=0,1,2,...这些时间点取样，至于为什么这样取样，我们就是这样规定的，f(t)=0.t<0，是有物理的可实现性。从模拟信号的拉普拉斯变换用

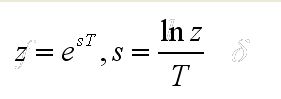
变换是不能直接变到Z变换的。因为Z变换必须是先采样。但是有一个留数法可以用，书上都有。我们来看看Z反变换,Z反变换其实就是

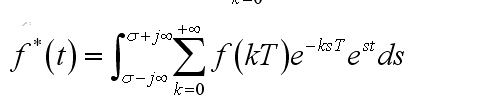
这里前面也少打了一个(1/2π），但是积分很难算，于是书上就给我们列一个表，让我们去查，同时，Z反变换还有一种留数法，我稍微来说一下这个东西，

乘以z^(k-1)就是为了构造z^(-1)，它的系数就是留数。

推荐链接，https://www.bilibili.com/video/av17409842