四种常见背包问题整理

四种常见背包问题整理

四种常见背包问题包括：① 最优装配 ② 部分背包问题 ③ 01背包问题 ④ 完全背包问题

① 最优装配

给出 n 个物体，重量分别为 w_i，使总重量不超过容量 C 的情况下选择尽量多的物体。

这种背包问题很简单，只要求数量多就可以，因此我们对重量进行排序贪心选择就好。

参考代码：

#include
#include
using namespace std;

int *stuff;

// 最优装配
int getResult(int n, int c){
	int cnt = 0;
	int sum = 0;
	for(int i = 0; i < n; i++){
		sum += stuff[i];
		if(sum <= c) cnt++;
		else break;
	}
	return cnt;
}

int main(){
	int n, c;
	while(cin >> n >> c){
		stuff = new int[n];
		for(int i = 0; i < n; i++){
			cin >> stuff[i];
		}
		sort(stuff, stuff+n);
		int cnt = getResult(n, c);
		cout << cnt << endl;
		delete[] stuff;
	} 
	return 0;
} 

② 部分背包问题

有 n 个物体，重量分别为 w_i，价值为 v_i，在总重量不超过容量 C 的情况下让总价值最高，

每个物体可以只取走一部分，若取走部分物体则价值也会等比例减少。

这种背包问题也比较简单，可以定义一个变量 rate 表示各个物体的性价比，

性价比最高的物体先拿走，如果可以整个物体都拿走则直接拿走，若不能整个拿走就拿走部分。

参考代码：

#include
#include
using namespace std;

struct STUFF {
	int weight;
	int price;
	double rate;  // 性价比
	bool operator < (STUFF other) const {
		return rate > other.rate;
	}
}*stuffs;

// 部分背包问题
double getResult(int n, int c){
	double sum = 0;
	for(int i = 0; i < n; i++){
        // 可以整个拿走就直接拿走
		if(c >= stuffs[i].weight){
			sum += stuffs[i].price;		
			c -= stuffs[i].weight;
		}
		else{
            // 不能直接拿走就拿部分
			sum += stuffs[i].price*1.0*c/stuffs[i].weight;
			break;
		}
	}
	return sum;
}

int main(){
	int n, c;
	while(cin >> n >> c){
		stuffs = new STUFF[n];
		for(int i = 0; i < n; i++){
			cin >> stuffs[i].weight >> stuffs[i].price;
			stuffs[i].rate = stuffs[i].price*1.0/stuffs[i].weight;
		} 
		sort(stuffs, stuffs+n);
		double result = getResult(n, c);
		cout << result << endl;
		delete[] stuffs;
	}
	return 0;
}

③ 01背包问题

有 n 个物体，重量分别为 w_i，价值为 v_i，在总重量不超过容量 C 的情况下让总价值最高，

但不允许只取走部分物体，要拿走只能整个拿走。

从01背包开始就涉及到了动态规划的知识，动态规划的本质就是递推。

先打表进行观察：

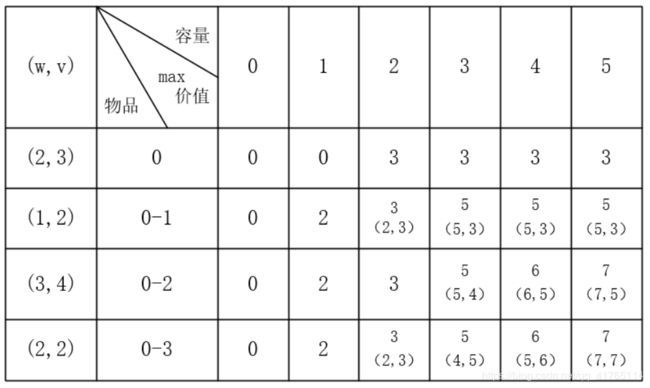
表中 dp[ i ] [ j ] 表示容量为 j，可以在 0 号物品到 i 号物品中进行任意组合，这种情况下的最大值。

第一行与第一列都不用说，一眼就可以直接得到答案。

剩下的部分怎么进行选择呢？

比如 dp[2] [4] = 6，我们已经知道了 dp[1] [4] = 5，说明在没有考虑 2 号物品的时候最大价值为 5。

现在加入了 2 号物品需要考虑，（3,4）重量为 3，价值为 4。

那么必须要选择 2 号物品才有可能超过之前计算不考虑 2 号物品的最大价值 5。

而选择 2 号物品的最大价值为多少呢？

应该是 dp[2-1] [4-3] + 4 = dp[1] [1] + 4 = 2 + 4 = 6，

dp[1] [1] 为不考虑 2 号物品，容量为 1 的最大价值，这样正好可以装下重量为 3 的 2 号物品且价值最大。

因此我们只要比较加入 2 号物品的最大价值与不加入 2 号物品的最大价值即可，

即 max(dp[1] [1] + 4, dp[1] [4])。

一般情况：dp[i] [j] = max( dp[i-1] [j-w] + v, dp[i-1] [j] )。

所以处理到最后 dp[2] [5] 就是我们要求的答案。

参考代码：

#include
#include
using namespace std;

int **stuffs;  // 物品数组 
int **dp;  // 二维数组保存dp表 

void show(int **arr, int n, int c){
	for(int i = 0; i < n; i++){
		for(int j = 0; j <= c; j++){
			cout << arr[i][j] << " ";
		}
		cout << endl;
	}
}

// 得到dp表 
int getDpTable(int n, int c){
	// 初始化第一行 
	for(int i = 0; i < c+1; i++){
		if(i >= stuffs[0][0]){
			dp[0][i] = stuffs[0][1];
		}
		else{
			dp[0][i] = 0;
		}
	}
	// 初始化第一列 
	for(int i = 0; i < n; i++){
		dp[i][0] = 0;
	} 
	// currentWeight和currentValue保存当前物品的重量与价值 
	int currentWeight, currentValue;
	for(int i = 1; i < n; i++){
		currentWeight = stuffs[i][0];
		currentValue = stuffs[i][1];
		for(int j = 1; j < c+1; j++){  // 注意i和j都是从1开始，j表示背包的容量
			if(j >= currentWeight){
				int value1 = currentValue+dp[i-1][j-currentWeight];  //  该物品的价值 + 没有加上该物品时的最大价值
				int value2 = dp[i-1][j];  // 使用前面i个物品组合成的最大价值 
				dp[i][j] = max(value1, value2);
			}
			else{
				dp[i][j] = dp[i-1][j];
			}
		}
	}
	show(dp, n, c);
	return dp[n-1][c];
}

int main(){
	int n, c;
	while(cin >> n >> c){
		stuffs = new int*[n];
		dp = new int*[n];
		for(int i = 0; i < n; i++){
			stuffs[i] = new int[2];
			dp[i] = new int[c+1];
		}
		for(int i = 0; i < n; i++){
			cin >> stuffs[i][0] >> stuffs[i][1];
		}
		cout << getDpTable(n, c) << endl;
		for(int i = 0; i < n; i++){
			delete[] stuffs[i];
			delete[] dp[i];
		}
		delete[] stuffs;
		delete[] dp;
	}
	return 0;
}

④ 完全背包问题

在01背包的基础上添加了新的条件：各个物品不再是一个，而是变成一种，可以拿多个。

继续打表观察：


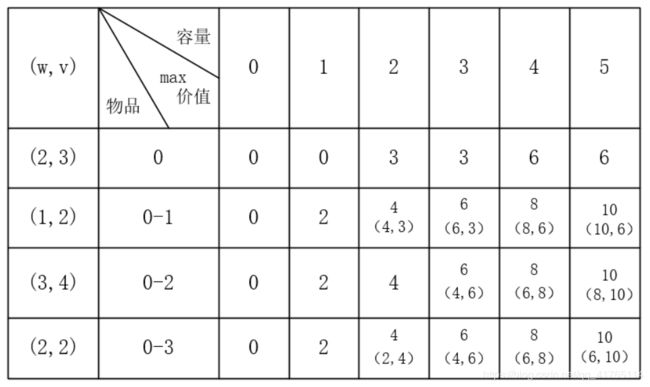
前面三种情况都很好分析，重点是最后一种情况。

这里的 v[i]+dp[i] [j-w[i]] 注意是 i 而不是01背包中的 i-1，是同一行。

虽然在完全背包中一个物品可以选择多个，但是并不需要通过 for 循环来确定选择 k 个 i 物品时价值最大。

我们只要简单分成两个状态就足够了： 1. 选择 i 物品 2. 不选择 i 物品

而 dp[i-1] [j] 就是不选择 i 物品时的最大价值 maxValue。

v[i] + dp[i] [j-w[i]] 是选择 i 物品时的最大价值maxValue，这里 v[i] 表示选择一个 i 物品，

但是选择一个 i 物品不保证是最大价值啊，这里就要看 dp[i] [j-w[i]] 了。

dp[i] [j-w[i]] 就已经包含了 k-1 个 i 物品的最大价值，因此两者组合起来就是 k 个 i 物品使总价值最大。

（01背包只能选一个，因此为 v[i] + dp[i-1] [j-w[i]]，

完全背包问题可以选多个，因此为 v[i] + dp[i] [j-w[i]]）

参考代码：

#include
#include
using namespace std;

struct STUFF {
	int weight;
	int value;
}*stuffs;

int **dp;

int getResult(int n, int c){
	for(int i = 1; i <= c; i++){
		dp[0][i] = (i/stuffs[0].weight)*stuffs[0].value;  // 初始化第一行 只能取第一个物品 
	}
	for(int i = 1; i < n; i++){
		for(int j = 1; j <= c; j++){
			if(stuffs[i].weight > j){
				dp[i][j] = dp[i-1][j];  // 如果买不起该物品 最大价值就是不买该物品时计算出来的最大值 
			}
			else{
				// 两种情况：1.买该物品 2.不买该物品
				// dp[i-1][j]就是不买该物品的最大价值
				// value[i]+dp[i][j-weight[i]]是买该物品时的最大价值 i物品被这里被选择了k次而不是1次 注意该重点 
				dp[i][j] = max(dp[i-1][j], stuffs[i].value+dp[i][j-stuffs[i].weight]);   
			}
		}
	}
	for(int i = 0; i < n; i++){
		for(int j = 0; j <= c; j++){
			cout << dp[i][j] << " ";
		}
		cout << endl;
	}
	return dp[n-1][c];
}

int main(){
	int n, c;
	while(cin >> n >> c){
		stuffs = new STUFF[n];
		dp = new int*[n];
		for(int i = 0; i < n; i++){
			dp[i] = new int[c+1];  // 注意是c+1 dp数组中有容量为0的情况 
		}
		for(int i = 0; i < n; i++){
			for(int j = 0; j <= c; j++){
				dp[i][j] = 0;
			}
		}
		for(int i = 0; i < n; i++){
			cin >> stuffs[i].weight >> stuffs[i].value;
		}
		int ans = getResult(n, c);
		cout << ans << endl;
		for(int i = 0; i < n; i++){
			delete[] dp[i];
		}
		delete[] dp;
		delete[] stuffs;
	}
	return 0;
} 

【END】感谢观看