FCM聚类与K-means聚类的分析比较
FCM聚类与K-means聚类的分析比较
- 一、FCM聚类
- 1.简介
- 2.FCM聚类算法原理
- 基本步骤
- 流程图
- 二、数据集介绍
- 1.数据集来源
- 2.详细介绍
- 三、FCM聚类实现
- 1.Matlab代码
- 2.运行结果(5次)
- 3.分析
- 四、K-means聚类实现
- 1.K-means算法基本原理
- 2.Matlab代码
- 3.运行结果(5次)
- 4.分析
- 五、对比分析
一、FCM聚类
1.简介
模糊C均值聚类(FCM),即模糊ISODATA,是用隶属度确定每个数据点属于某个聚类的程度的一种聚类算法。1973年,Bezdek提出了该算法,作为早期硬C均值聚类(HCM)方法的一种改进。
模糊数学是用数学方法研究和处理具有“模糊性”现象的数学。
模糊正如其字面意思,就是不清晰。比如:“今天天气很热”,它的范围难以准确定义。若要判断10°C、45°C是否是“天气很热”,答案自然是明确的!但要判断28°C-35°C左右的气温是否属于“天气很热”的集合, 就不那么好确定了。
2.FCM聚类算法原理
设有限样本集(论域)X={X1,X2,…,XN},每一个样本与s个特征Xj={Xj1,Xj2,…,X~js},即样本的特征矩阵:

欲把它分为K类(2≤K≤N),则N个样本划分为K类的模糊分类矩阵为:

其满足下列三个条件:
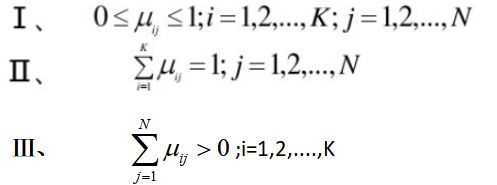
条件Ⅱ表明每一样本属于各类的隶属度之和为1 ;条件Ⅲ表明每一类模糊集不可能是空集合,即总有样本不同程度的隶属于某类。
定义K个聚类中心Z={Z1,Z2,…,ZK}。其中Zi={Zi1,Zi2,…,Zis};i=1,2,…,K 。

第i类的中心Z,即人为假想的理想样本,它对应的s个指标值是该类样本所对应的指标值的平均值:
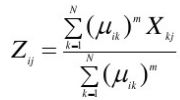
构造准则函数:
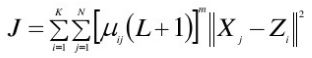
其中,||Xj-Zi||表示第j个样本与第i类中心之间的欧式距离; J表示所有待聚类样本与所属类的聚类中心之间距离的平方和。
为了确定最佳分类结果,就是寻求最佳划分矩阵U和对应的聚类中心Z ,使J达到极小。
基本步骤
(1)选择初始聚类中心Zi(0)
(2)计算初始隶属度矩阵U(0)
(3)求各类的新的聚类中心Zi(L)
(4)计算新的隶属度矩阵U(L+1)
(5) 回到第(3)步,重复至收敛
(6)类别调整:①合并②分解③删除
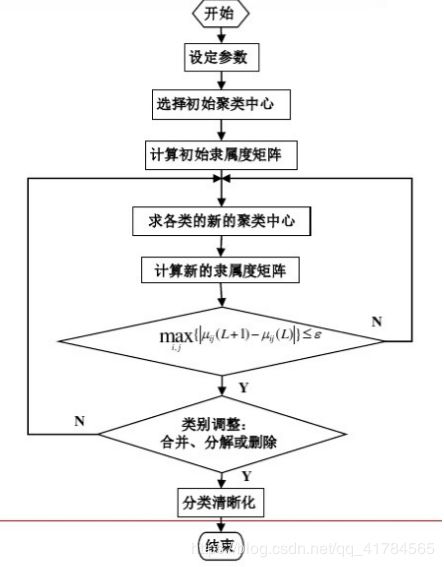
流程图
二、数据集介绍
1.数据集来源
数据采自UCI数据库,UCI数据库是加州大学欧文分校(University of CaliforniaIrvine)提出的用于机器学习的数据库,这个数据库目前共有335个数据集,其数目还在不断增加,UCI数据集是一个常用的标准测试数据集。
本数据集来自网址:http://archive.ics.uci.edu/ml/datasets/Wine+Quality
2.详细介绍
摘要
这个数据集是来自葡萄牙北部的红葡萄酒样品有关的数据集,与葡萄牙“ Vinho Verde”葡萄酒的红色变体有关。
由于隐私和物流问题,仅物理化学(输入)和感觉(输出)变量可用(例如,没有有关葡萄类型,葡萄酒品牌,葡萄酒售价等的数据)。
输入内容包括客观测试(例如PH值),输出内容基于感官数据(葡萄酒专家至少进行3次评估的中位数)。每位专家对葡萄酒质量进行评分在0(非常差)和10(非常好)之间。

相关信息
1.实例数量:2024。
2.属性数量:11 +输出属性
注意:几个属性可能是相关的,因此应用某种形式的功能选择。
3.属性信息:
输入变量(基于理化测试):
1-固定酸度
2-挥发性酸度
3-柠檬酸
4-残留糖
5-氯化物
6-游离二氧化硫
7-总二氧化硫
8-密度
9-pH
10-硫酸盐
11-酒精
输出变量(基于感官数据):
12-质量(得分在0到10之间)
4.缺少属性值:无
三、FCM聚类实现
1.Matlab代码
数据存放形式为每行用分号隔开,如下:

需读到程序中去,数据导入:
fid=fopen('wine.txt');
spec='%f %f %f %f %f %f %f %f %f %f %f %f ';
quality=textscan(fid,spec,'Delimiter',';');
data=zeros(2024,11);
flag=zeros(1,11);
for i=1:2024
k=1;
for j=1:11
flag(1,k)=quality{1,j}(i,1);
k=k+1;
end
data(i,:)=flag;
end
FCM聚类:
T=100;
c=11;
m=2;
[U, V]=myfcm(data, c, T, m, epsm);
function [U, V,objFcn] = myfcm(data, c, T, m, epsm)
% fuzzy c-means algorithm
% 输入: data: 待聚类数据,n行s列,n为数据个数,s为每个数据的特征数
% c : 聚类中心个数
% m : 模糊系数
% 输出: U : 隶属度矩阵,c行n列,元素uij表示第j个数据隶属于第i类的程度
% V : 聚类中心向量,c行s列,有c个中心,每个中心有s维特征
if nargin < 3
T = 100; %默认迭代次数为100
end
if nargin < 5
epsm = 1.0e-6; %默认收敛精度
end
if nargin < 4
m = 2; %默认模糊系数值为2
end
[n, s] = size(data);
% 初始化隶属度矩阵U(0),并归一化
U0 = rand(c, n);
temp = sum(U0,1);
for i=1:n
U0(:,i) = U0(:,i)./temp(i);
end
iter = 0;
V(c,s) = 0; U(c,n) = 0; distance(c,n) = 0;
while( iter<T )
iter = iter + 1;
% U = U0;
% 更新V(t)
Um = U0.^m;
V = Um*data./(sum(Um,2)*ones(1,s)); % MATLAB矩阵相乘
% 更新U(t)
for i = 1:c
for j = 1:n
distance(i,j) = mydist(data(j,:),V(i,:));
end
end
U=1./(distance.^m.*(ones(c,1)*sum(distance.^(-m))));
objFcn(iter) = sum(sum(Um.*distance.^2));
% FCM算法停止条件
if norm(U-U0,Inf)<epsm
break
end
U0=U;
end
myplot(U,objFcn);
function d = mydist(X,Y)
% 计算向量Y到向量X的欧氏距离的开方
d = sqrt(sum((X-Y).^2));
end
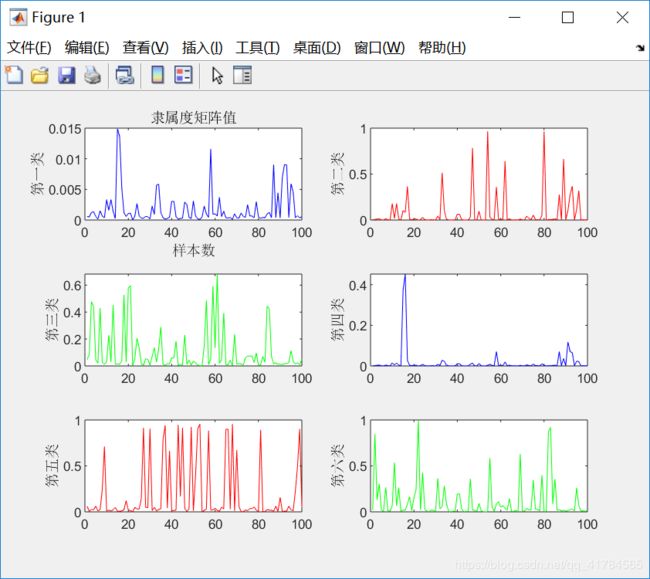
function myplot(U,objFcn)
% 将隶属度U矩阵可视化
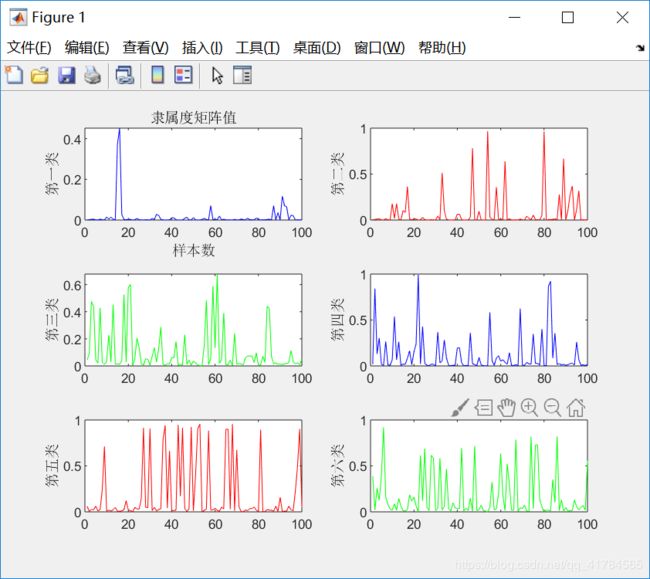
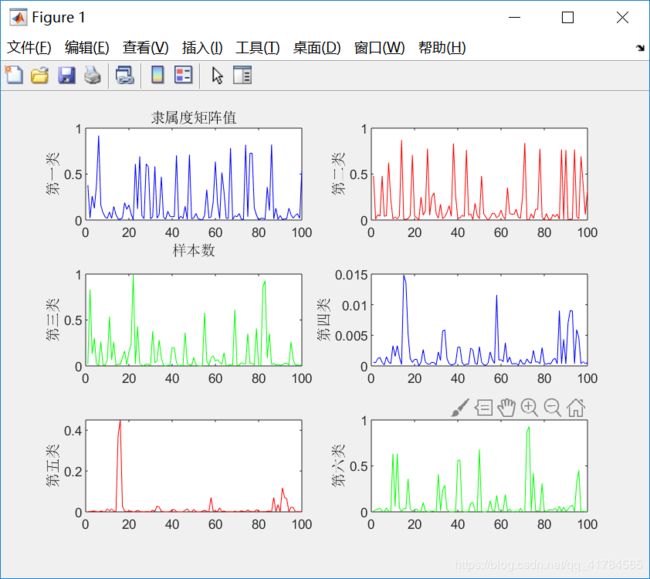
figure(1)
subplot(3,2,1);
plot(U(1,1:100),'-b');
title('隶属度矩阵值')
ylabel('第一类')
xlabel('样本数')
subplot(3,2,2);
plot(U(2,1:100),'-r');
ylabel('第二类')
subplot(3,2,3);
plot(U(3,1:100),'-g');
ylabel('第三类')
subplot(3,2,4);
plot(U(4,1:100),'-b');
ylabel('第四类')
subplot(3,2,5);
plot(U(5,1:100),'-r');
ylabel('第五类')
subplot(3,2,6);
plot(U(6,1:100),'-g');
ylabel('第六类')
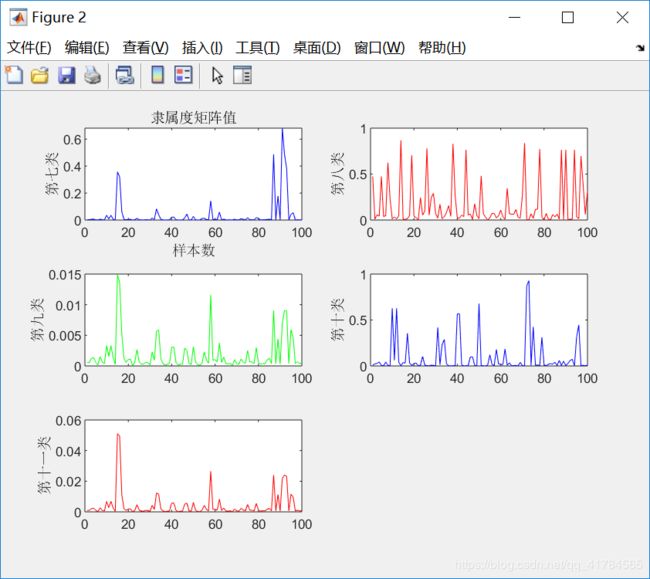
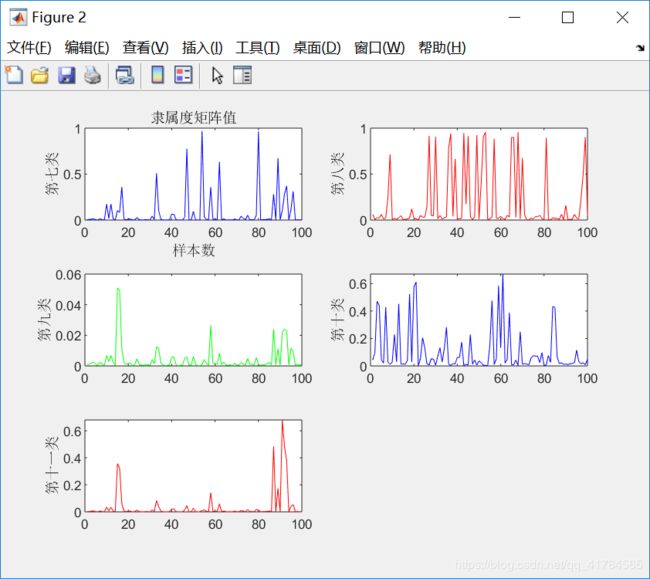
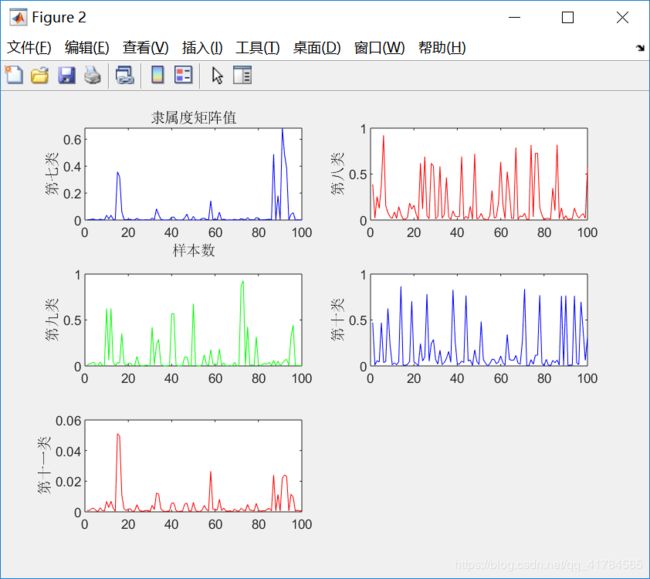
figure(2)
subplot(3,2,1);
plot(U(7,1:100),'-b');
title('隶属度矩阵值')
ylabel('第七类')
xlabel('样本数')
subplot(3,2,2);
plot(U(8,1:100),'-r');
ylabel('第八类')
subplot(3,2,3);
plot(U(9,1:100),'-g');
ylabel('第九类')
subplot(3,2,4);
plot(U(10,1:100),'-b');
ylabel('第十类')
subplot(3,2,5);
plot(U(11,1:100),'-r');
ylabel('第十一类')
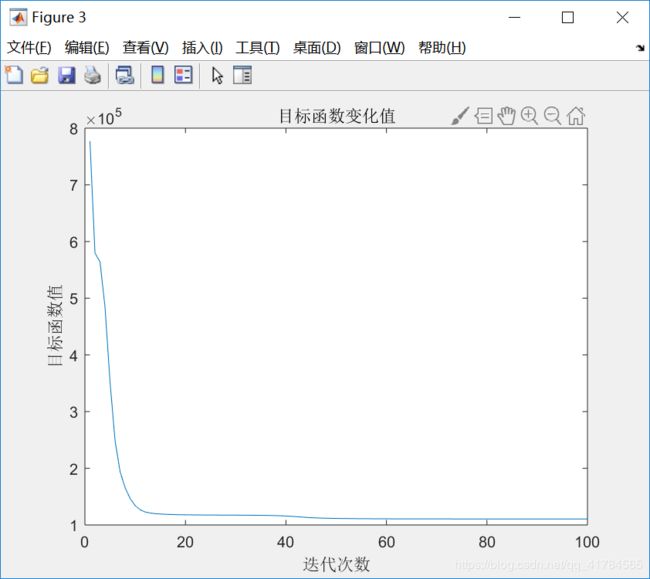
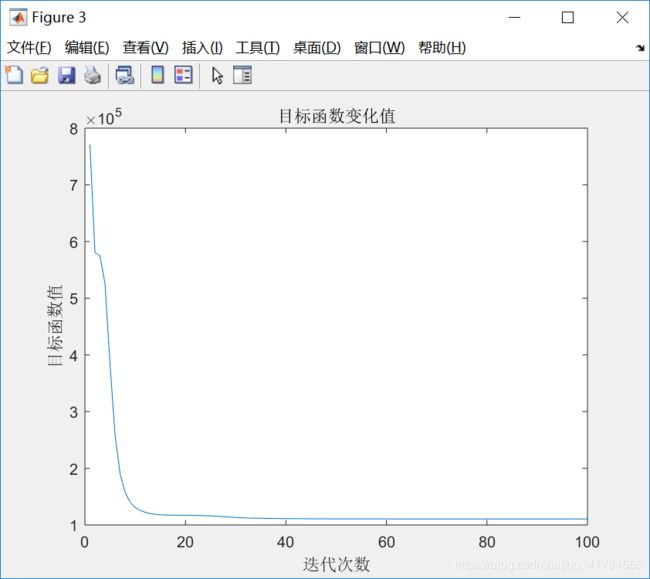
figure(3)
grid on
plot(objFcn);
title('目标函数变化值');
xlabel('迭代次数')
ylabel('目标函数值')
end
end
计算平均模糊熵:
Fuzzy=0;%平均模糊熵
for i=1:c
for j=n
Fuzzy=Fuzzy+U(i,j)*log(U(i,j));
end
Fuzzy=Fuzzy/n;
end
disp('平均模糊熵:');
disp(Fuzzy);
2.运行结果(5次)
First:
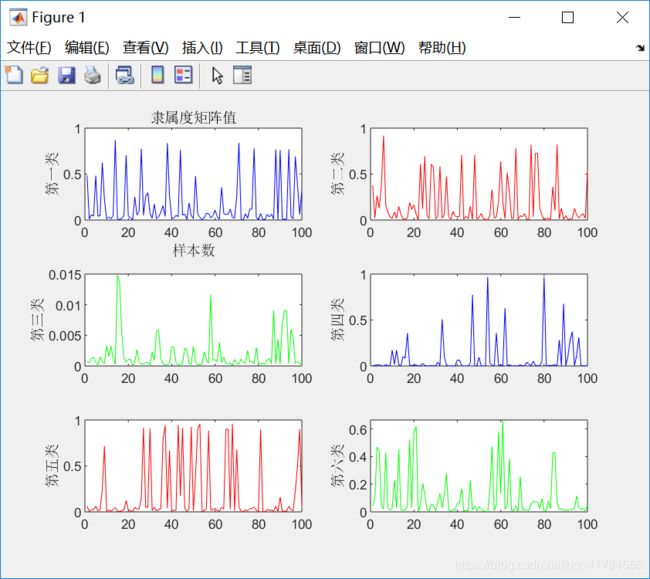
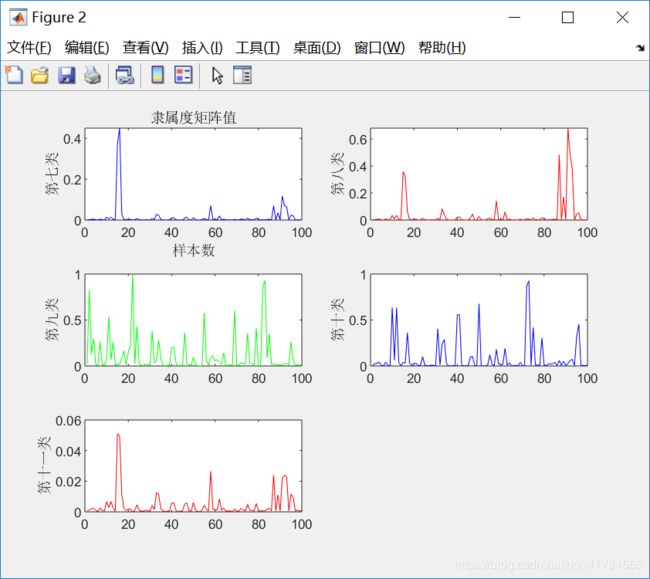
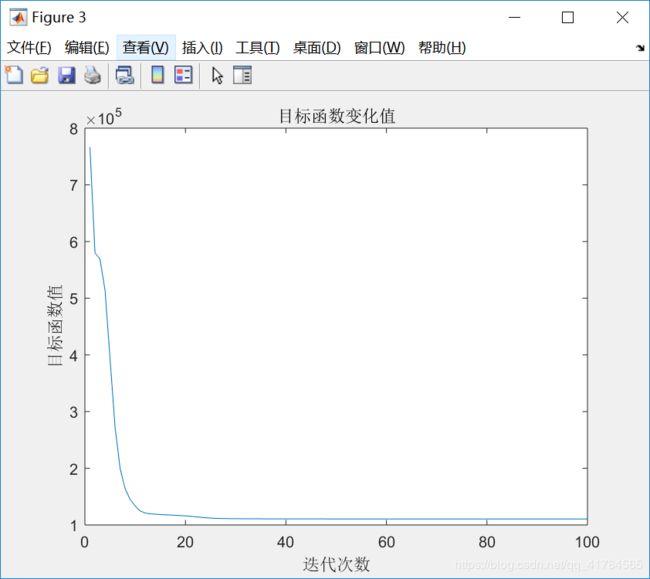
隶属度矩阵U(部分):
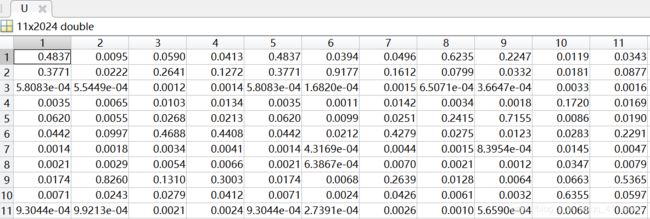
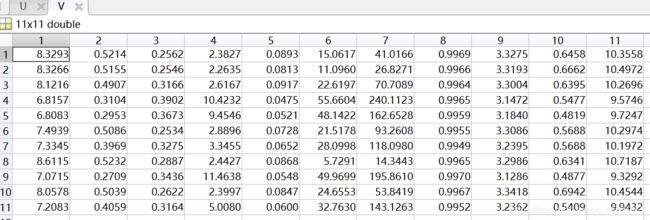
聚类中心V:
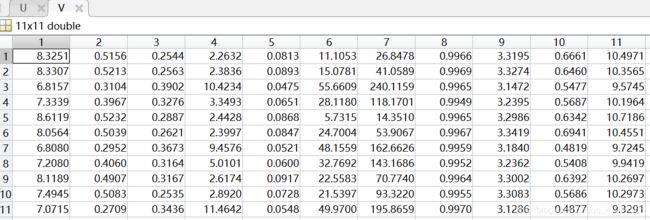
Second:
隶属度矩阵U(部分):
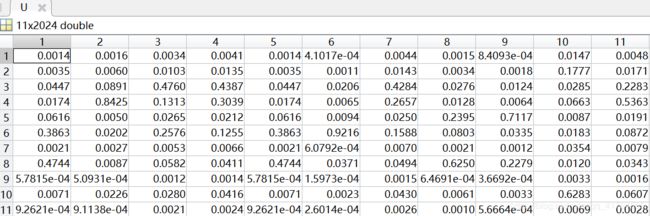
聚类中心V:
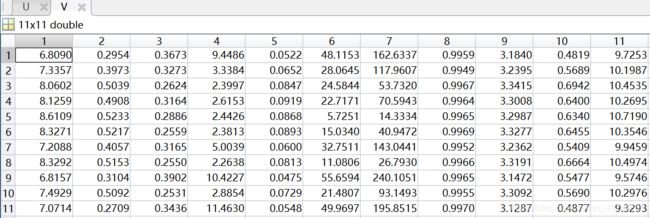
Third:

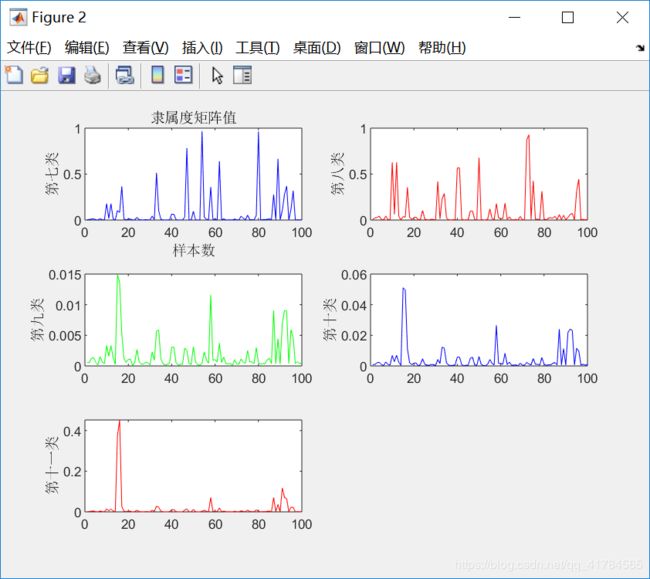
隶属度矩阵U(部分):
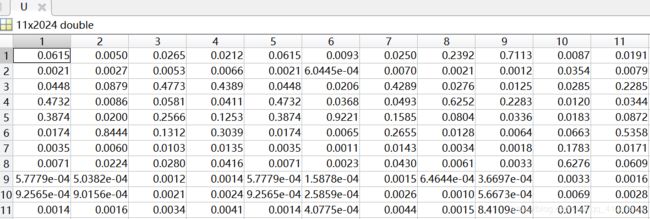
聚类中心V:
Fourth:
隶属度矩阵U(部分):
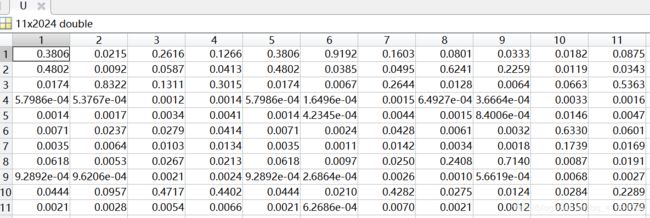
聚类中心V:
Fifth:
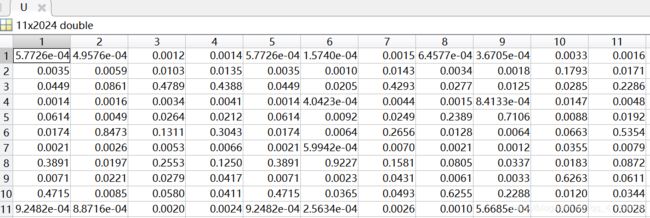
隶属度矩阵U(部分):
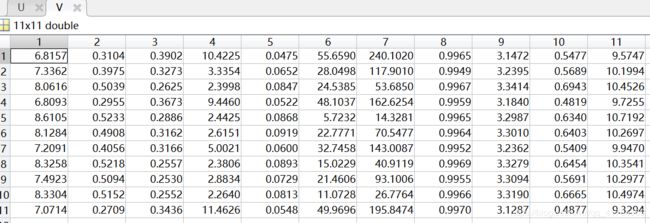
聚类中心V:
3.分析
①采用FCM算法对红酒的质量进行模糊聚类,因为专家对酒的质量进行打分范围在0(非常差)~10(非常好)之间,所以对酒的质量分类分为11类,因此设定c=11。即数据样本总数为2024,每个样本有11个特征,将这些样本划分为11类。根据上述结果展示可知,由于每次给定的初始值不同,对结果有较大影响,因此运行5次可以得到互不相同的结果,从目标函数变化趋势图可以看出,大约迭代了20次左右,目标函数开始收敛,隶属度矩阵值图展示前100个样本的隶属情况,从隶属度矩阵U可以看出样本分类情况,从聚类中心向量V可以看到c行s列,即c个中心,每个中心s维特征。
②聚类效果检验:利用平均模糊熵作检验,此处取模糊系数q=2,运行5次结果如下表所示,当平均模糊熵越接近0,聚类效果越好,所以从下表的数值可以看出该聚类效果较好。
| 运行次数 | 平均模糊熵(Fuzzy) |
|---|---|
| 1 | -2.4796e-06 |
| 2 | -1.5831e-06 |
| 3 | -2.1778e-06 |
| 4 | -6.5958e-07 |
| 5 | -2.3892e-06 |
③运行速度检验:利用Matlab的“运行并计时”功能,计算运行时间:

运行5次,得到运行时间如下表所示:
| 运行次数 | 函数(wine)总时间 |
|---|---|
| 1 | 7.017s |
| 2 | 7.468s |
| 3 | 7.046 s |
| 4 | 6.881s |
| 5 | 7.505s |
四、K-means聚类实现
1.K-means算法基本原理
k均值聚类算法(k-means clustering algorithm)是一种迭代求解的聚类分析算法。其实现过程如下:
第一步:从文件中读取数据,点用元组表示;确定聚类个数k。
第二步:初始化k个聚类中心。在所获得的的样本区间范围内随机产生k个值作为初始质心。
第三步:对每个数据点进行分类,选择相似度最高的质心所在的簇作为该样本的类别,形成k个簇。
第四步:计算每个簇中所有点的平均值,更新聚类中心。
第五步:迭代3~4步,直至聚类中心不再更改或达到最大迭代次数,算法结束。
2.Matlab代码
与上述FCM聚类算法实现一样,首先进行数据导入(主程序):
fid=fopen('wine.txt');
spec='%f %f %f %f %f %f %f %f %f %f %f %f ';
quality=textscan(fid,spec,'Delimiter',';');
data=zeros(2024,11);
flag=zeros(1,11);
for i=1:2024
k=1;
for j=1:11
flag(1,k)=quality{1,j}(i,1);
k=k+1;
end
data(i,:)=flag;
end
[ subCenter,centroids ] = kMeans1(data, 11);
随机选取质心:
function [ centroids ] = randCent( dataSet, k ) %% 取得随机中心
[m,n] = size(dataSet);%取得列数
centroids = zeros(k, n);
for j = 1:n
minJ = min(dataSet(:,j));
rangeJ = max(dataSet(:,j))-min(dataSet(:,j));
centroids(:,j) = minJ+rand(k,1)*rangeJ;%产生区间上的随机数
end
end
计算相似性:
function [ dist ] = distence( vecA, vecB )
dist = (vecA-vecB)*(vecA-vecB)';%这里取欧式距离的平方
end
K-means主程序:
function [ subCenter,centroids ] = kMeans1( dataSet, k ) %% kMeans的核心程序,不断迭代求解聚类中心
[m,n] = size(dataSet);
%初始化聚类中心
centroids = randCent(dataSet, k);
subCenter = zeros(m,2); %做一个m*2的矩阵,第一列存储类别,第二列存储距离
change = 1;%判断是否改变
while change == 1
change = 0;
%对每一组数据计算距离
for i = 1:m
minDist = inf;
minIndex = 0;
for j = 1:k
dist= distence(dataSet(i,:), centroids(j,:));
if dist < minDist
minDist = dist;
minIndex = j;
end
end
if subCenter(i,1) ~= minIndex
change = 1;
subCenter(i,:)=[minIndex, minDist];
end
end
%对k类重新计算聚类中心
for j = 1:k
sum = zeros(1,n);
r = 0;%数量
for i = 1:m
if subCenter(i,1) == j
sum = sum + dataSet(i,:);
r = r+1;
end
end
if r~=0
centroids(j,:) = sum./r;
end
end
end
end
3.运行结果(5次)
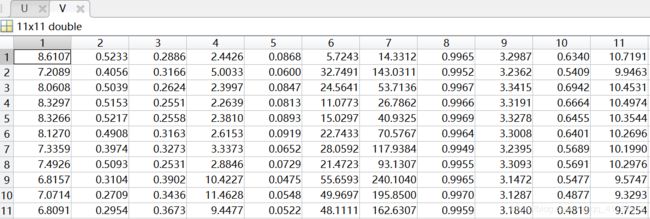
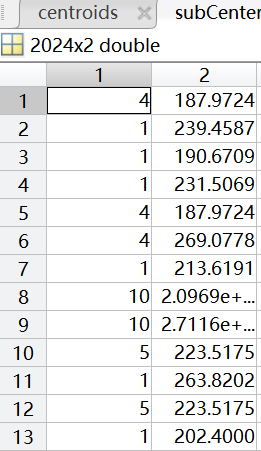
聚类中心用矩阵centroids表示,聚类情况用矩阵subCenter表示(其中第一列表示该样本所属类别(共11类),第二列表示样本到聚类中心的距离)。
First:
聚类中心:
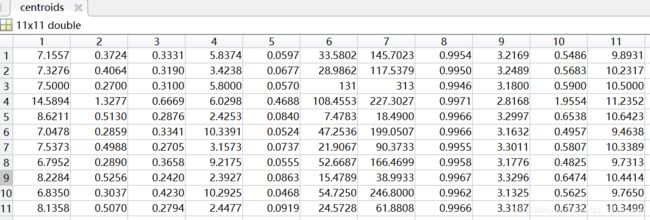
聚类情况(部分):
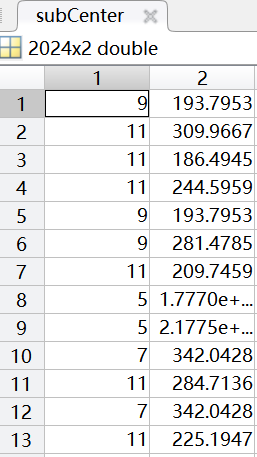
Second
聚类中心:
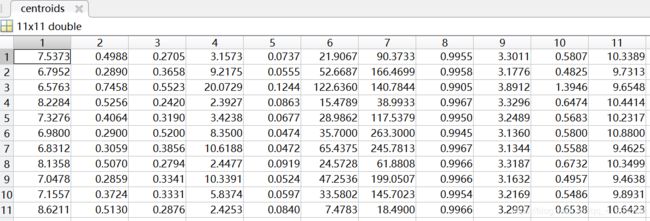
聚类情况(部分):
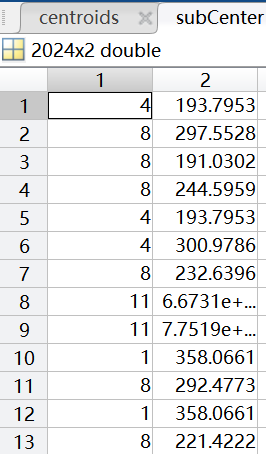
Third
聚类中心:
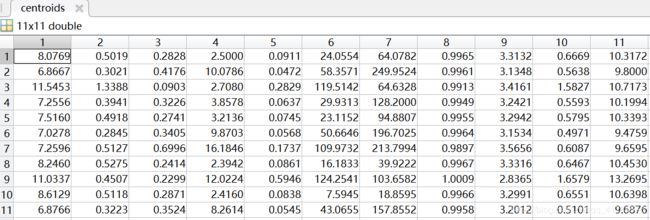
聚类情况(部分):
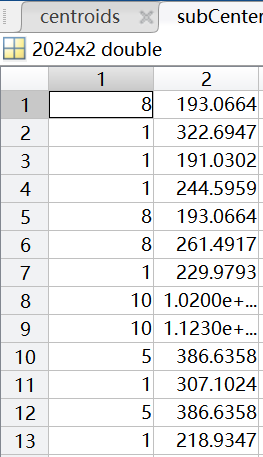
Fourth
聚类中心:
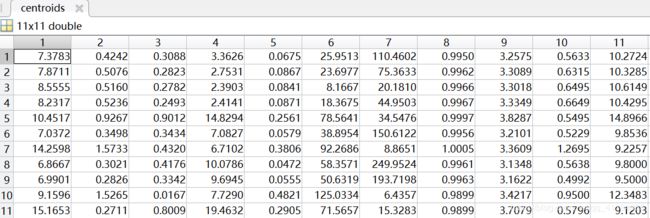
聚类情况(部分):
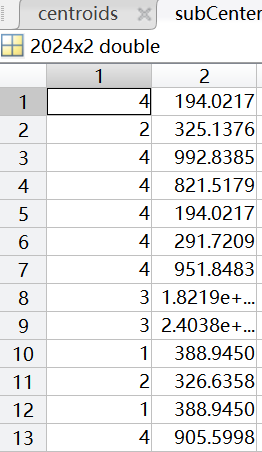
Fifth
聚类中心:
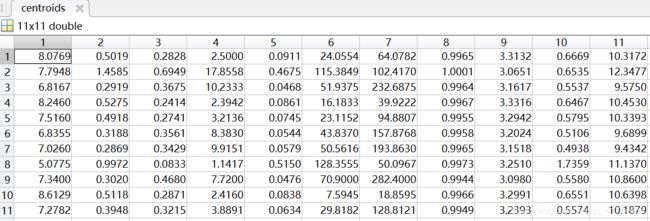
聚类情况(部分):
4.分析
采用K-means算法对数据进行聚类,多次迭代,多次更新聚类中心点,计算各簇平均值,直至聚类中心不再更改或达到最大迭代次数,算法结束,得到最终结果。
同样将数据分为11类(0~10级),聚类中心用矩阵centroids表示,矩阵的行表示类别,列表示样本的维度,即11×11;聚类情况用矩阵subCenter表示,其中行表示每个样本,第一列表示该样本所属类别(共11类),第二列表示样本到聚类中心的距离,通过比对原数据的标签,可以得到准确率大约在40%-60%。
运行速度检验:利用Matlab的“运行并计时”功能,计算运行时间,运行5次,得到运行时间如下表所示:
| 运行次数 | 函数(kmeans11)总时间 |
|---|---|
| 1 | 3.164s |
| 2 | 3.243s |
| 3 | 4.051 s |
| 4 | 3.693s |
| 5 | 4.034s |
五、对比分析
1.K-Means算法的原理很简单,对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。K-means的主要优点:原理简单,实现容易,收敛速度快,算法的可解释度比较强。但是,对于K-means算法,K值的选取不好把握;对于不是凸的数据集比较难收敛;采用迭代方法,得到的结果只是局部最优;对噪音和异常点比较的敏感。
2.ISODATA算法(即FCM聚类算法)是由K-均值算法发展而来的一种重要的聚类分析算法,这种算法对特性比较复杂而人们又缺少认识的对象进行分类,可以有效地实施人工干预,加入人脑思维信息,使分类结果更符合客观实际,可以给出相对的最优分类结果,因而具有一定的实用性。然而该算法同样存在不足之处,主要有:需要设定一些参数,若参数的初始化选取的不合适,可能影响聚类结果的正确性;当数据样本集合较大并且特征数目较多时,算法的实时性不太好。
3.速度比较:从上述两种聚类结果分析中可得,FCM聚类代码运行时间大约为7.2s,K-means聚类代码运行时间大约在3.6s。因为FCM聚类需要经过更多次的迭代,计算量大,数据更加细腻,因此速度会稍慢些,而K-means聚类数据简单,速度快。
4.精度比较:由于本次实验所找的数据集本身带有标签,已做好分类,所以将实验结果同原有数据做比较,可以看出K-means聚类准确率大约在40%-60%,FCM聚类准确度大约在45%-70%,求得其平均模糊熵约为-2e-06,聚类效果较好,可得FCM聚类的精度会稍高于K-means。