个人笔记-《数字图像处理》(冈萨雷斯) 第三版- 第二章 数字图像基础（二）

在数字图像处理领域，《数字图像处理(第三版)》作为主要教材已有30多年。这是目前笔者个人所记录的笔记，后续会不断更新。若要获取本书pdf版本以及更多python，深度学习，机器学习，计算机视觉等高清PDF以及 个人笔记的 word版本，可在微信公共号“分享猿”获取资源。

13.阵列相乘&矩阵相乘
阵列相乘

矩阵相乘

备注：之后所用基本上都是阵列(array)相乘

14.算子
算子 H 对给定的输入图像 f(x,y) ，产生一幅输入图像 g(x,y)：

如果

则称 H 是一个线性算子

15.算术操作
图像间数算操作是阵列操作,在相应像素之间执行。

下面是几个算术操作在图像处理中的例子
① 针对降噪的带噪声图像相加(平均)
令 g(x,y) 是无噪图像 f(x,y) 被加性噪声 η(x,y) 污染后的图像，即

这里假设在每对坐标(x,y)处，噪声是不相关的，并且其均值为零。以下步骤的目的是通过组带噪图像{ g_i (x,y) }的相加减少噪声。

然后，遵循

和

随着K的增大，在每个位置 (x,y) 处的像素值的变化(就像方差或标准差度量的那样)将减小。因为E{g ̅(x,y)}= f(x,y)，这意味着在求平均过程中所使用的带噪图像的数量K增加时，g ̅(x,y) 将通近 f(x,y)。

② 增强差别的图像相减
图像相减经常作用于增强图像之间的差
g(x,y)= f(x,y)-h(x,y)

③ 使用图像相乘和相除来校正阴影
图像相乘(或相除)的一种重要应用是阴影校正。
g(x,y)= f(x,y) ·h(x,y)
f(x,y) 表示完美图像，h(x,y) 表示阴影函数

图像相乘的另一种普通应用时模板操作，也称感兴趣区域(ROI)操作
模板图像的ROI区域为1，其他区域为0

16.灰度范围改变
大多数图像用8比特(RGB也是3个8比特通道)显示，灰度值范围为0~255
下面的操作将其他范围的转为特定 √K 比特数（范围是[0，K]）

在处理8比特图像时，置K = 255，得到一灰度范围为[0，255]的全部8比特的满标度图像。
另外在执行除法操作时，需要将较小的数加到图像像素上，以免用0去除。

17.集合操作
交∩、并∪、补 A^C={├ ω┤|w∉A} = U -A 差
图像灰度的集合操作 – 有些区别
令灰度级图像的元素用集合A来表示，这些元素是(x,y,z)，x,y是坐标，z为灰度值，
A的补集定义为 A^C={(x,y,K-z) | x,y,z∈A}
两个灰度集合A和B的并集可定义为集合

下面的三幅图展示了灰度级图像的集合操作

原图像、使用补集获得的负像、前两副图像的并集

获取此三张高清图片以及这部分 代码实现 可在文章开头的公众号内 回复“骨骼“获取

18.逻辑操作

或OR且AND非NOT分别对应集合操作中的交并补
AND-NOT 对应集合操作的减
XOR 异或

逻辑操作广泛用于图像的形态学处理

19.模糊集合
前述的集合和逻辑结果是“干脆”的概念，在这种意义下，元素要么是要么不是集合中的成员。这在某些应用中受到严重限制。
假如我们希望把世界上的所有人分为年轻人和非年轻人。使用“干脆”的集合，令U代表所有的人，令A是U的子集，表示年轻人集合。为了形成集合A。我们需要个隶属度函数，该函数可以对U中的每个元素(人)赋1值或0值。隶属度函数简单地定义为个阅值，低于该阔值的人考虑为年轻人。高于该阔值的人考虑为非年轻人。
模糊集合理论使用隶属度函数来实现这种概念，该函数在数值1(定义为年轻)和0(定义为非年轻)之间逐步过渡。使用模糊集合，我们可以声明个人的年轻度为50% (年轻和非年轻过渡的中间)。换句话说，年龄是个不精确的概念，而模糊逻辑提供处理这种概念的工具。

20.空间操作
空间操作之间在给定图像的像素上执行，我们把空间操作分为三大类
(1)单像素操作
(2)邻域操作
(3)几何空间变换

单像素操作
s=T(z) - T为变换函数

邻域操作
令 s_xy 表示输入图像 f 中任一点(x,y)为中心的一个邻域的坐标集。
输出图像 g 在经过特定操作后形成。
假如该操作是 计算大小为m*n、中心在(x,y)的矩形邻域中的像素平均值。可由下式表达：

几何空间变换
包括以下两个步骤：
(1)坐标的空间变换

(2)灰度内插
最近邻、双线性、双三次

最常用的空间坐标变换之一是仿射变换，其一般形式如下：


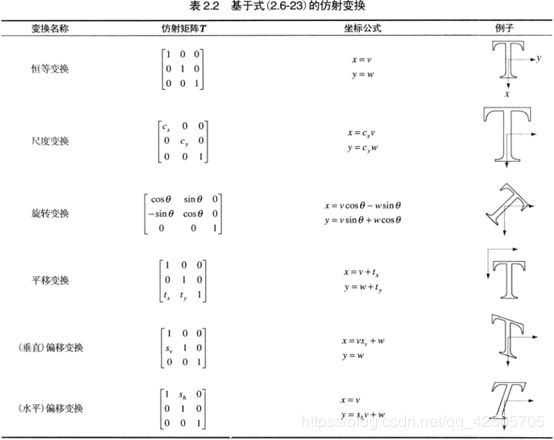
两种方法使用上式：
前向映射
反向映射(更有效)

21.图像配准
在图像配准中，根据输入图像和输出图像(参考图像)找到特定变换T
约束点(控制点)：在输入图像和参考图像中其位置恰好已知的相应点。

22.向量和矩阵操作
整个图像可当作矩阵(或向量)来处理，这是很重要的。
如，将一MN图像描述为MN1维向量，之后可用下列表示图像的线性处理：
g = Hf + n
f 表示输入图像的MN1向量，n 表示MN噪声模式的MN1向量，g 表示处理后图像的MN1向量，H 是用于对输入图像进行线性操作的MN*MN矩阵。
上式对图像复原有帮助。

23.图像变换



除傅里叶变换之外，还有沃尔什变换、哈达玛变换、离散余弦变换、哈尔变换和斜变换等。

24.概论方法
均值和方差对于图像的视觉特效有明显的直接关系，高阶矩更敏感。