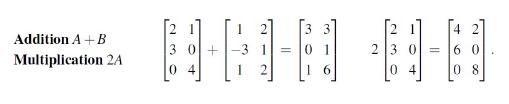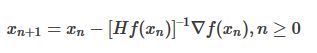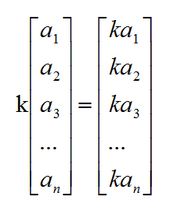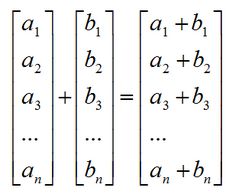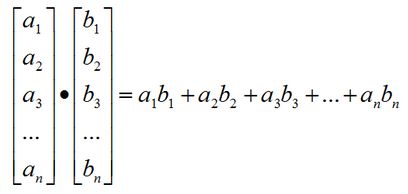机器学习中的数学(四)--线性代数
写在前面
《机器学习中的数学》系列主要列举了在机器学习中用到的较多的数学知识,包括微积分,线性代数,概率统计,信息论以及凸优化等等。本系列重在描述基本概念,并不在应用的方面的做深入的探讨,如果想更深的了解某一方面的知识,请自行查找研究。
第四部分主要讲述了机器学习过程中应用比较多的线性代数知识,主要包括向量及其运算,矩阵及其运算,特征值与特征向量,常用的矩阵和向量求导以及主成分分析等。
1.矩阵运算
1.1 矩阵的加减
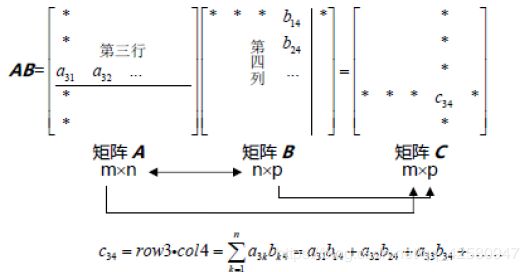
1.2 矩阵的乘法
矩阵乘法的标准计算方法是通过矩阵A第i行的行向量和矩阵B第j列的列向量点积得到的:
举例为:
注意:矩阵没有除法,矩阵的除法想当于乘以矩阵的逆矩阵.
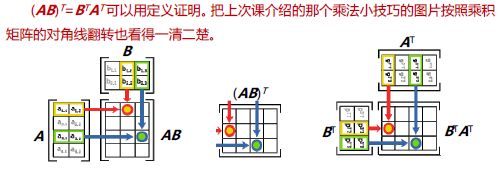
2. 矩阵的转置
3. 矩阵的逆
4. 矩阵的求导
说明:关于对x的求导的结果为什么是矩阵A的转置而不是矩阵A本身,个人理解是:对矩阵或者对向量求导,实际上就是对矩阵或者向量的每一元素分别求导,至于怎么排列只是为了计算方便。换句话说,求导结果可以使矩阵A也可以是矩阵A的转置,这取决与之后怎么运算比较方便。
5. 海森矩阵(Hessian Matrix)
凸函数的海森矩阵是半正定的(特征值都是大于等于0的)。
牛顿法中就用到了海森矩阵。
6. 向量极其运算
6.1 向量与标量
虽然向量与标量不能相加减,但是可以相乘,至于标量与向量的除法可以看做乘以标量的导数。其几何解释为:向量乘以标量或者除以标量,相当于因子k来缩放向量的长度。
向量的加法和减法的前提:如果两个向量的维数相同,那么他们能够相加减,运算结果的向量的维数和原向量相同。向量的加法等于两个向量的分量相加,向量的减法相当于加上一个负向量。
向量极其运算的几何意义:
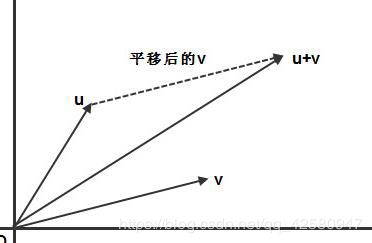
向量加法的几何意义:
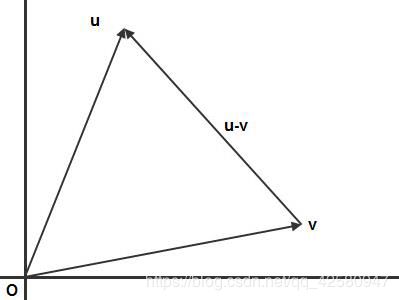
向量减法的几何意义:
6.2 向量与向量(内积).
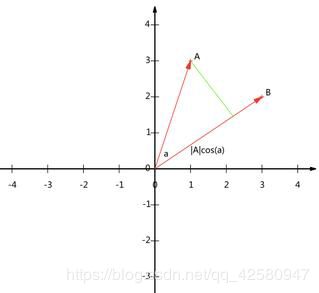
向量与向量的乘法称为向量的内积,如下图所示:
点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及b向量在a向量方向上的投影,如果两个向量垂直,内积则为零。
举例:
如果|B|=1,则上式可以转化成如下式子:
也就是说,设向量B的模为1,则A与B的内积值等于A向B所在直线投影的矢量长度。如下图所示:
6.3 向量的相关性
如果向量满足如下式子
仅当:
![]()
时才成立,则称向量是线性无关的。在二维空间中,两个向量只要不在一条直线上就是线性无关的。在三维空间中,三个向量线性无关的条件是是他们不在一个平面上。
6.4 空间的维数和基
维数:通俗的定义一下空间的维数即每一点的元素个数,例如:(1,2,3)是三维空间的一个点;(1,2)是二维空间的一个点。
基:我们可以通俗的认为,基就是“坐标系”。n维空间的计是由n个线性无关的向量构成,没有最好的基,只有最合适的基。我们要根据不同的情况建立不同的基。
7. 主成分分析
主成分分析是一种统计方法,是通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
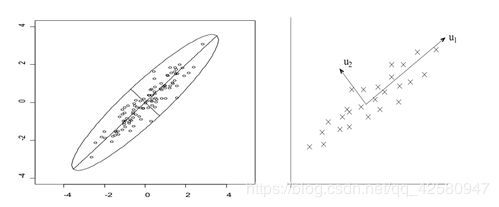
主成分分析的目的是将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来代替原来的指标。如上图所示,左边的一组数据在标准的直角坐标系中具有一定的相关性,但是如果选择如右图所示的基之后,在v1和v2上的数据的投影的方差具有明显的差异,这就将元数据分解成一组新的互相无关的指标。
其原理就是对原始的空间中顺序地找一组相互正交的坐标轴,第一个轴是使得方差最大,第二个轴是在与第一个轴正交的平面中使得方差最大,这样假设在N维空间中,我们可以找到N个这样的坐标轴。我们取前r个去近似这个空间,这样就从一个N维的空间压缩到r维的空间了,但是我们选择的r个坐标轴能够使得空间已经压缩的数据的损失最小。
8.特征值
如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式:
![]()
这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式:
A必须为实对称矩阵,实对称矩阵才有正交基让其对角化。
特征值分解在机器学习中的应用:在机器学习特征提取中,意思就是最大特征值对应的特征向量方向上包含最多的信息量,如果某几个特征值很小,说明这几个方向信息量很小,可以用来降维,也就是删除小特征值对应方向的数据,只保留大特征值方向对应的数据,这样做以后数据量减小,但有用信息量变化不大,PCA降维就是基于这种思路。