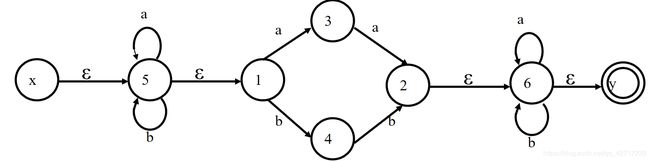
编译原理 第四章 学习笔记1
FA—有穷自动机—Finite Automata
NFA—不确定的有穷自动机—Nondeterministic Finite Automata
DFA—确定的有穷自动机—Deterministic Finite Automata
| DFA | a | b | F |
|---|---|---|---|
| [x51] | [513] | [514] | |
| [513] | [51326y] | [514] | |
| [514] | [513] | [51426y] | |
| [51326y] | [51326y] | [5146y] | 1 |
| [51426y] | [5136y] | [51426y] | 1 |
| [5146y] | [5136y] | [51426y] | 1 |
| [5136y] | [51326y] | [5146y] | 1 |
| DFA | a | b | F |
|---|---|---|---|
| 0 | 1 | 2 | |
| 1 | 3 | 2 | |
| 2 | 1 | 4 | |
| 3 | 3 | 5 | 1 |
| 4 | 6 | 4 | 1 |
| 5 | 6 | 4 | 1 |
| 6 | 3 | 5 | 1 |

2、FA与正则文法的关系
定理1:对任意的正则文法G=( VN, VT, P, S),都存在一个有穷自动机A,使得L(A)=L(G)
定理2:对任一DFA(或NFA),都存在一个正则文法G,使L(G)=L(A)
具体步骤:
(1)对于 A->a的产生式,按归约理解,句子中的第1个字符,都是用A->a的产生式进行归约的.对应到FA中,FA从开始状态出发,读到句子的第一个字符a,将它归约为A。此时引入初态 q, 定义为:f(q,a)=A.
(2)对于 A->Ba的产生式,FA应该在状态B读入 a,其状态转为A , 即 f(B,a)=A. 也可理解为在状态B时,FA已将当前句子处理过的前缀归约成了B,此时它读入 a时,要将Ba归约为A。
(3)按归约来说,如果一个输入串是文法G产生语言的合法句子,它最终应该被归约成开始符号。所以G的开始符号就是FA M的终止状态。
【EG】构造下述文法G[S]的自动机:
S—>A0 (1)
A—>A0 | S1 | 0 (2)
该自动机是确定的吗?若不确定,则对它确定化。该自动机相应的语言是什么?
| NFA | 0 | 1 | F |
|---|---|---|---|
| q | A | ||
| A | AS | ||
| S | A | 1 |
| DFA | 0 | 1 | F |
|---|---|---|---|
| [q]-1 | [A]-2 | ||
| [A]-2 | [AS]-3 | ||
| [AS]-3 | [AS]-3 | [A]-2 | 1 |
3、正则式与FA的等价性
【EG】已知L(G)={x | x 属于{0,1}* ,且不含两个相邻的1}, 求文法G。
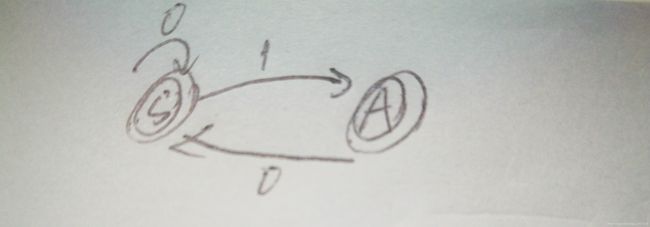
画出对应的FA,可知文法为:
S—>0S | 1A | 空
A—>0S | 空
两个定理:
(1)对于上的NFA M,可构造一个上的正则式r,使L®=L(M);
(2)对于上的每个正则式r,可构造上的NFA M,使L(M)=L®。
【EG】已知FA,求正则式
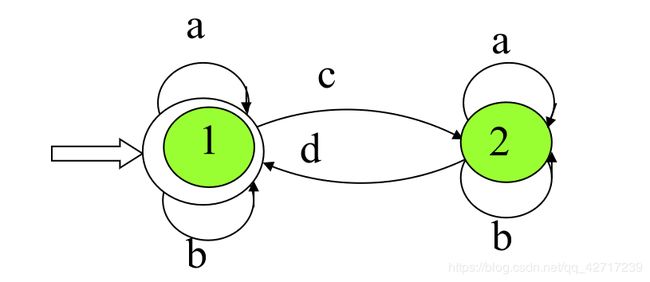
正则式:(a | b | c (a|b)* d)*
【EG】已知FA,求正则式。
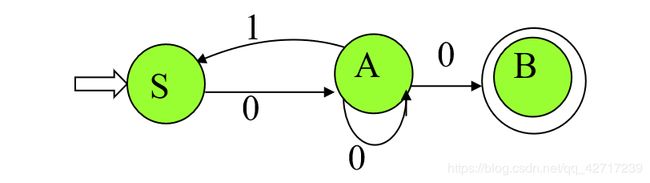
正则式:0(0 | 10)*0
简单的解释一下:S->A和A->B的是两个不可省略的过程,也就是我们写出正则式前后的两个0,所以所有的文章都出在A上面,所以我们只需要看A要经历哪些状态再次回到A,才能保证S顺利的到达B。A可以一直0循环,也可以先到S再回来并且不断循环,所以(0|10) *。由此我们可以确定正则式。
4、正则式构造等价NFA
【EG】已知正则式r=b*(d|ad)(b|ad)+构造等价的NFA M。

【EG】已知正则式r= 1 (01) * (0* | 1* ) 0 ,构造等价的NFA M。

5、DFA的化简(DFA最小化)
1.化简的FA:是指没有多余状态且状态中没有两个是互相等价的。
2.多余状态:从DFA的开始状态出发,任何输入串也不能到达的那个状态。
3.在DFA中,状态s和t状态等价的条件是:
(1)一致性条件——s和t必须同时为可接受态或不可接受态。
(2)蔓延性条件——对于所有输入符号, s和t必须转换到等价的状态集里。
如果DFA的状态s和t不等价,则称s和t是可区分的。
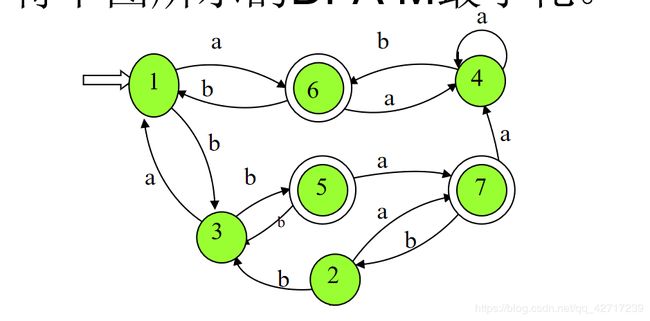
| a | b | F | |
|---|---|---|---|
| 1 | 6 | 3 | |
| 2 | 7 | 3 | |
| 3 | 1 | 5 | |
| 4 | 4 | 6 | |
| 5 | 7 | 3 | 1 |
| 6 | 4 | 1 | 1 |
| 7 | 4 | 2 | 1 |
接下来划分集合
P=({1,2,3,4},{5,6,7})=({1,2},{3,4},{5},{6,7})=({1,2},{3},{4},{5},{6,7})
1、2相同,6、7相同

【EG】把图确定化、最小化
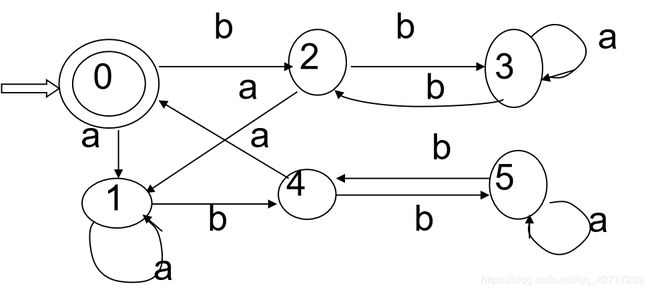
| DFA | a | b | F |
|---|---|---|---|
| 0 | 1 | 2 | 1 |
| 1 | 1 | 4 | |
| 2 | 1 | 3 | |
| 3 | 3 | 2 | |
| 4 | 0 | 5 | |
| 5 | 5 | 4 |
P=({0},{1,2,3,4,5})=({0},{4},{1,2,3,5})=({0},{4},{1,5},{2},{3})
所以1和5是等价的