《算法概论》实验—图：用最大流与最小割算法解决实际问题

最大流问题：
在最大流问题中，容量c和流量f满足3个性质：
容量限制：For each e ∈E：0≤f(e)≤c(e)
斜对称性：f(u,v)=-f(v,u)
流量平衡：For each v ∈V –{s, t}: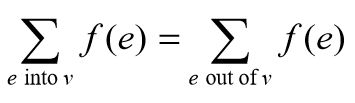
求解最大流问题的算法：增广路径算法。
算法思想：从所有边的流量均为0开始不断增加流量，保持每次增加流量后都满足容量限制、斜对称性和流量平衡三个条件.
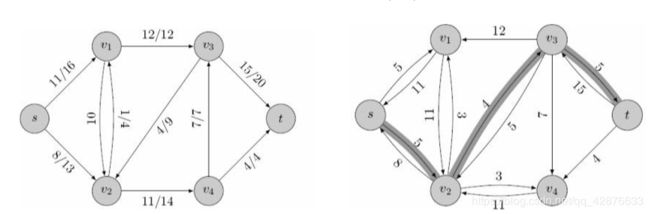
计算出每条边上容量与流量之差（残量），得到残量图，其中将流量值作为反向边的流量值，如下图所示。

                                

显然，残量图中的边数可以达到原图中的两倍。如原图中c=16，f=11的边在 残量网络中对应正反两条边，残量分别为16-11=5和0-(-11)=11（回顾前面讲的，残量：每条边上容量与流量之差）。

残量边这里还有待补充的，我感觉自己还没很清楚，看图可以知道，已经有的流值直接加在了反向边上，残量才是顺着往前的

前面说了，算法的思想是：在满足那三个条件的情况下，从所有边的流量均为0开始不断增加流量。这就是增广的过程：找到所有从s到t的道路上，所有残量最小的值d（瓶颈值），然后把对应所有边上流量增加d即可。不难验证，如果增广前的流量满足3个 条件，增广后仍然满足。显然，只要残量网络中存在增广路，流量就可以增大。可以证明它 的逆命题也成立：如果残量网络中不存在增广路，则当前流就是最大流。这就是著名的增广路定理。

最小割最大流定理

s-t割：把所有顶点分成两个集 合S和T=V-S，其中源点s在集合S中，汇点t在集合T中。如果把“起点在S中，终点在T中”的边全部删除，就无法从s到达t了。这样的集合划分 (S,T)称为一个s-t割。

割的容量：即起点在S中，终点在T中的所 有边的容量和。

从另外一个角度看待割，从s运送到t的物品必然通过跨越S和T的 边，所以从s到t的净流量等于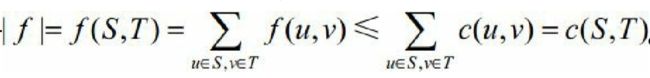

这个很好算。由此可以得出结论： 对于任意s-t流f和任意s-t割(S, T)，有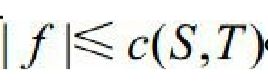 

下面来看残量网络中没有增广路的情形。既然不存在增广路，在残量网络中s和t并不连通（回顾前面讲的增广路）。当BFS没有找到任何s-t道路时，把已标号结点（a[u]>0的结点u）集合看成S，令T=V-S， 则在残量网络中S和T分离，因此在原图中跨越S和T的所有弧均满载（这样的边才不会存在于 残量网络中），且没有从T回到S的流量（这个是为啥），因此成立|f|≤(S,T)成立

一、二部图最大匹配（Bipartite Matching）
 

#include
#include
#include
#include
using namespace std;
const int MAX_L = 20;
const int MAX_R = 20;
const int MAXN = 40;
const int INF = 1000000;
int L, R;
bool can[MAX_L][MAX_R];//可以匹配信息的存储
struct Edge
{ 
    int from, to, cap, flow;
    Edge(int u, int v, int c, int f) :from(u), to(v), cap(c), flow(f){} 
};
    int n, m;
    vector edges;//边数的两倍
    vector G[MAXN];// //邻接表，G[i][j]表示结点i的第j条边在e数组中的序号 
    int a[MAXN];                //起点到i的最小残量
    int p[MAXN];                //最短路树上p的入弧编号
    void init(int n)
    {
        for (int i = 0; i < n; i++)
            G[i].clear();
        edges.clear();
    }
    void AddEdge(int from, int to, int cap)
    {
        edges.push_back(Edge(from, to, cap, 0));
        edges.push_back(Edge(to, from, 0, 0)); //反向弧,这里有个技巧，每条弧和对应的反向弧保存在一起，按照这个存储，边i的反向边是i^1   
        m = edges.size();
        G[from].push_back(m - 2);//再加入一条从点from出发的边，因为新加的边和反向边已经加到edges里了，所以序号为m-2 ，下同
        G[to].push_back(m - 1);
    }
    int Maxflow(int s, int t) {
        int flow = 0;//初始化最大流是0
        for (;;)
        {
            memset(a, 0, sizeof(a)); //初始时残量自然为0  
            queue Q;
            Q.push(s);//将起始点加入栈中     
            a[s] = INF;
            while (!Q.empty())
            {
                int x = Q.front();
                Q.pop(); //取出栈顶元素    
                for (int i = 0; i < G[x].size(); i++)//遍历栈顶元素的所有边 
                {
                    Edge& e = edges[G[x][i]];//e为栈顶点的第i条边  
                    if (!a[e.to] && e.cap > e.flow)//如果到达这条边的邻接点路径的最小残量残量不为0（有增广路径）且边的容量大于流值 
                    {
                        p[e.to] = G[x][i];//G[i][j]表示结点i的第j条边在e数组中的序号 ,p[e.to]里存的是这个序号  
                        a[e.to] = min(a[x], e.cap - e.flow);//到这条边终点的最小残量等于到点x的最小残量和当边e残量的最小值  
                        Q.push(e.to);//处理完之后将栈顶元素在该边的邻接点也加入到栈中，如此下来，所有栈顶元素能产生增广路径的邻接点都会加到栈里
                    }
                }
                if (a[t]) break;//当栈为空，或者
            }
            if (!a[t]) break; //到达终点的路径残量为0时，for循环终止
            for (int u = t; u != s; u = edges[p[u]].from)//从点t开始回溯
            {
                edges[p[u]].flow += a[t];//给每条路径的流值加上最小残量    
                edges[p[u] ^ 1].flow -= a[t];//给每条路径的反向边的流值减去这个最小残量 
            }
            flow += a[t];//给最大流加上最小残量 
        }
        return flow;
    }
void solve()
    {
    int s = L + R, t = s + 1;//main中需要有的数据：L,R，左右的个数，还有bool can[MAX_N][MAX_K];
    for (int i = 0; i < L; i++)
    {
        AddEdge(s, i, 1);
    }
    for (int i = 0; i < R; i++)
    {
        AddEdge(L + 1, t, 1);
    }
    for (int i = 0; i < L; i++)
    {
        for (int j = 0; j < R; j++)
        {
            if (can[i][j])
            {
                AddEdge(i, L + j, 1);
            }
        }
    }
    printf("%d\n", Maxflow(s, t));
}
int main()
{
    cin >> L >> R;
    for (int i = 0; i < L; i++)
    {
        for (int j = 0; j < R; j++)
        {
            cin >> can[i][j];
        }
    }
    solve();
    return 0;
}
/*
5 5
1 1 0 0 0
0 1 0 0 0
1 0 1 1 0
0 1 0 0 1
0 1 0 0 1
最大匹配数应该是4
*/

二、项目选择（Project Selection）
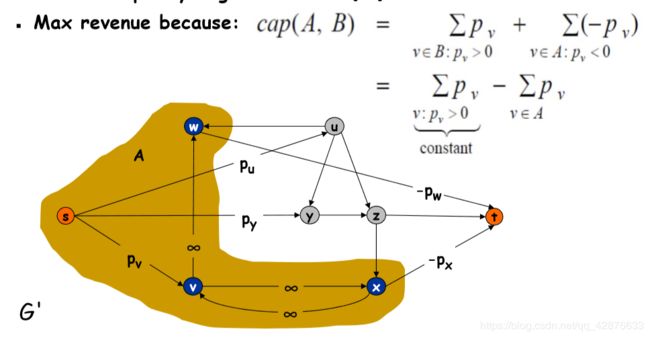
算法思想：将最大问题（最大收益）转换成最小问题（最小割），为什么呢？让我们来看一个推导：

cap(A-B)=a1-a2，显然a1是一个常数，a2就是项目的收益，我们如果想要让a2达到最大，那么cap(A-B)自然要最小，于是问题就转换成了求最小割，最后最小割求出来，只要将最小割里的pv值加起来就可以了。

#include
#include
#include
#include
using namespace std;
const int MAX_V = 50;
const int MAXN = 100;
const int INF = 1000000;
int V;
int L, R;
bool can[MAX_V][MAX_V];//可以匹配信息的存储
int val[MAX_V];
struct Edge
{
	int from, to, cap, flow;
	Edge(int u, int v, int c, int f) :from(u), to(v), cap(c), flow(f) {}
};
int n, m;
vector edges;//前向边和反向边的合集 
vector G[MAXN];// //邻接表，G[i][j]表示结点i的第j条边在e数组中的序号 
int a[MAXN];                //起点到i的最小残量
int p[MAXN];                //最短路树上p的入弧编号
void init(int n)
{
	for (int i = 0; i < n; i++)
		G[i].clear();
	edges.clear();
}
void AddEdge(int from, int to, int cap)
{
	edges.push_back(Edge(from, to, cap, 0));
	edges.push_back(Edge(to, from, 0, 0)); //反向弧,每条弧和对应的反向弧保存在一起，按照这个存储，边i的反向边是i^1   
	m = edges.size();
	G[from].push_back(m - 2);//再加入一条从点from出发的边，因为新加的边和反向边已经加到edges里了，所以序号为m-2 ，下同
	G[to].push_back(m - 1);
}
void Maxflow(int s, int t) {
	int flow = 0;//初始化最大流是0
	for (;;)
	{
		memset(a, 0, sizeof(a)); //初始时残量自然为0  
		queue Q;
		Q.push(s);//将起始点加入栈中     
		a[s] = INF;
		while (!Q.empty())
		{
			int x = Q.front();
			Q.pop(); //取出栈顶元素    
			for (int i = 0; i < G[x].size(); i++)//遍历栈顶元素的所有边 
			{
				Edge& e = edges[G[x][i]];//e为栈顶点的第i条边  
				if (!a[e.to] && e.cap > e.flow)//如果到达这条边的邻接点路径的最小残量残量为0且边的容量大于流值，意思就是没有访问过的边 
				{
					p[e.to] = G[x][i];//G[i][j]表示结点i的第j条边在e数组中的序号 ,p[e.to]里存的是这个序号  
					a[e.to] = min(a[x], e.cap - e.flow);//到这条边终点的最小残量等于到点x的最小残量和当边e残量的最小值  
					Q.push(e.to);//处理完之后将栈顶元素在该边的邻接点也加入到栈中，如此下来，所有栈顶元素能产生增广路径的邻接点都会加到栈里
				}
			}
			if (a[t]) break;//如果栈不空或者到达点t的路径中残量不为零（找到了增广路径），就终止循环，否则就继续
		}
		if (!a[t]) break; //到达终点的路径残量为0时。及不存在增广路径时，for循环终止，否则执行下面的过程
		for (int u = t; u != s; u = edges[p[u]].from)//从点t开始回溯
		{
			edges[p[u]].flow += a[t];//给每条路径的流值加上最小残量    
			edges[p[u] ^ 1].flow -= a[t];//给每条路径的反向边的流值减去这个最小残量 
		}
		flow += a[t];//给最大流加上最小残量 
	}
	//return flow;
}
void solve()
{
	int s = V, t = V + 1;//main中需要有的数据：L,R，左右的个数，还有bool can[MAX_N][MAX_K];
	for (int i = 0; i < V; i++)
	{
		if (val[i] > 0)
		{
			AddEdge(s, i, val[i]);
		}
		else
			AddEdge(i, t, -val[i]);
	}
	for (int i = 0; i < V; i++)
	{
		for (int j = 0; j < V; j++)
		{		
			if (can[i][j])
			{
				AddEdge(i, j, INF);
			}
		}
	}
	Maxflow(s, t);
	int count = 0;
	printf("最佳项目选择的方案为：");
	for (int i = 0; i < V; i++)//这样刚好不算s和t
	{
		if (a[i] > 0)
		{
			count += val[i];
			printf("%d ", i + 1);//项目命名比数组多一
		}
	}
	printf("\n最佳收益为：%d",count);
}
int main()
{
	cin >> V;
	for (int i = 0; i < V; i++)
	{
		for (int j = 0; j < V; j++)
		{
			cin >> can[i][j];
		}
	}
	for (int j = 0; j < V; j++)
	{
		cin >> val[j];
	}
	solve();
	return 0;
}
/*
6
0 1 0 1 1 0
0 0 0 0 1 0
0 0 0 1 0 1
0 0 0 0 0 0
0 0 0 0 0 1
0 0 1 0 0 0
8 10 7 -6 -4 -3
*/

三、调查设计（Survey Design）
我哭泣了，还是不会，先搁这儿

（目前仅作为个人总结，内容还有待完善）