分支定界法(matlab实现)

分支定界法

背景

今天利用matlab来实现求解完全整数规划问题和混合整数规划问题的分支定界法。
这里求解的模型为目标函数最小化模型:

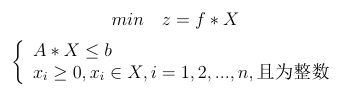
基本理论

• 分支定界法：用以求解整数规划问题的一种方法。
• 求解步骤：
  首先我们规定求解的整数规划问题为A，相应的线性规划问题为B

1. 对问题B进行求解
   1. 若B无可行解，则A也无可行解，停止计算
   2. 若B有最优解，且符合整数条件，该最优解为A的最优解，停止计算
   3. 若B有最优解，但不符合整数条件，记它的目标函数值为z*，作为最优值的下界
2. 找出问题A的一个整数可行解，其目标函数值作为最优解的上界
3. 进行迭代
   1. 分支，在B的最优解中任选一个不符合整数条件的变量$x_j$，其值为$b_j$，构造两个约束条件，$x_j\le [b_j]$、$x_j\ge [b_j]+1$，分别加入到问题B中，形成两个子问题$B_1$、$B_2$。不考虑整数条件求解这两个子问题。即分支
   2. 定界。对每个后继问题表明其求解的结果，与其他问题进行比较，将最优目标函数值最小者（不包括问题B）作为新的下界，在已符合整数条件的各分支中，找出目标函数值最小者作为新的上界。
   3. 剪枝，将目标函数值不在上界、下界中的分支剪去
   4. 重复1 2 3，直到得到最优解
      注意事项：在对两分支进行分解时，优先选择目标函数值最小的分支进行分解。

分支定界法中，通过定界进而进行剪枝，对分支进行了筛选，使我们仅在一部分可行解中寻求最优解，而不是全部穷举出来再寻找，其求解效率更高。

代码实现

因为分支定界法的求解过程与二叉树结构相同，所以我们利用二叉树这种数据结构来存储每一个线性规划问题的解及对应的目标函数值。

代码如下：

1. 首先是主函数：

% main.m
% 分支定界法
% -----------------------------------------------
% 求解模型：
% min z = f * x
% A * x <= b
% x >= 0,且为整数
% ---------------------------------------------------
clear global;
clear;
clc;

global result; % 存储所有整数解
global lowerBound; % 下界
global upperBound; % 上界
global count; % 用以判断是否为第一次分支

count = 1;

f = [-40, -90];
A = [8, 7;
    7, 20;];
b = [56; 70];
Aeq = [];
beq = [];
lbnd = [0; 0];
ubnd = [inf; inf];

BinTree = createBinTreeNode({f, A, b, Aeq, beq, lbnd, ubnd});
if ~isempty(result)
    [fval,flag]=min(result(:,end)); % result中每一行对应一个整数解及对应的函数值
    Result=result(flag,:);
    disp('该整数规划问题的最优解为：');
    disp(Result(1,1:end-1));
    disp('该整数规划问题的最优值为：');
    disp(Result(1,end));
else
    disp('该整数规划问题无可行解');
end

2. 创建二叉树函数

% createBinTreeNode.m
% 构建二叉树，每一结点对应一解
function BinTree = createBinTreeNode(binTreeNode)

global result;
global lowerBound;
global upperBound;
global count;

if isempty(binTreeNode)
    return;
else
    BinTree{1} = binTreeNode;
    BinTree{2} = [];
    BinTree{3} = [];
    
    [x, fval, exitflag] = linprog(binTreeNode{1}, binTreeNode{2}, binTreeNode{3}, ...
        binTreeNode{4}, binTreeNode{5}, binTreeNode{6}, binTreeNode{7});
    if count == 1
%         upperBound = 0; % 初始下界为空
        lowerBound = fval;
        count = 2;
    end
    
    if ~IsInRange(fval)
        return;
    end

    if exitflag == 1
        flag = [];
        % 寻找非整数解分量
        for i = 1 : length(x)
            if round(x(i)) ~= x(i)
                flag = i;
                break;
            end
        end
        % 分支
        if ~isempty(flag)
            lowerBound = max([lowerBound; fval]);
            OutputLowerAndUpperBounds();
            lbnd = binTreeNode{6};
            ubnd = binTreeNode{7};
            lbnd(flag, 1) = ceil(x(flag, 1)); % 朝正无穷四舍五入
            ubnd(flag, 1) = floor(x(flag, 1));
            
            % 进行比较，优先选择目标函数较大的进行分支
            [~, fval1] = linprog(binTreeNode{1}, binTreeNode{2}, binTreeNode{3}, ...
        binTreeNode{4}, binTreeNode{5}, binTreeNode{6}, ubnd);
            [~, fval2] = linprog(binTreeNode{1}, binTreeNode{2}, binTreeNode{3}, ...
        binTreeNode{4}, binTreeNode{5}, lbnd, binTreeNode{7});
            if fval1 < fval2                
                % 创建左子树          
                BinTree{2} = createBinTreeNode({binTreeNode{1}, binTreeNode{2}, binTreeNode{3}, ...
            binTreeNode{4}, binTreeNode{5}, binTreeNode{6}, ubnd});

                % 创建右子树
                BinTree{3} = createBinTreeNode({binTreeNode{1}, binTreeNode{2}, binTreeNode{3}, ...
            binTreeNode{4}, binTreeNode{5}, lbnd, binTreeNode{7}});
            else
                % 创建右子树
                BinTree{3} = createBinTreeNode({binTreeNode{1}, binTreeNode{2}, binTreeNode{3}, ...
            binTreeNode{4}, binTreeNode{5}, lbnd, binTreeNode{7}});
                % 创建左子树          
                BinTree{2} = createBinTreeNode({binTreeNode{1}, binTreeNode{2}, binTreeNode{3}, ...
            binTreeNode{4}, binTreeNode{5}, binTreeNode{6}, ubnd});
            end
        else
            upperBound = min([upperBound; fval]);
            OutputLowerAndUpperBounds();
            result = [result; [x', fval]];
            return;
        end
    else
        % 剪枝
        return;
    end  
end

3. 判断目标函数值是否在上下界范围中

% IsInRange.m
% 判断分支问题的解是否在上下界的范围中，若不在，剪去
function y = IsInRange(fval)
    global lowerBound;
    global upperBound;

    if isempty(upperBound) & fval >= lowerBound
        y = 1;
    else if  (fval >= lowerBound & fval <= upperBound)
        y = 1;
    else
        y = 0;
    end
end

4. 打印输出上下界

% 打印输出上下界
function y = OutputLowerAndUpperBounds()

global lowerBound;
global upperBound;

disp("此时下界、上界分别为");
disp(lowerBound);
if isempty(upperBound)
    disp('  无上界')
else
    disp(upperBound);
end

end

计算实例

• 计算结果如下：