梯度下降法(Gradient Descent)
梯度下降法(Gradient Descent)
- 梯度下降法
- 批量梯度下降法
- 随机梯度下降法
- scikit-learn中的随机梯度下降法
- 小批量梯度下降法
梯度下降法
梯度下降法,不是一个机器学习算法(既不是再做监督学习,也不是非监督学习,分类、回归问题都解决不了),是一种基于搜索的最优化方法。
梯度下降法作用是,最小化一个损失函数;而如果我们要最大化一个效用函数,应该使用梯度上升法。

这个二维平面描述了,当我们定义了一个 损 失 函 数 J 损失函数J 损失函数J 后,那么每取一个 参 数 t h e t a 参数theta 参数theta, 损 失 函 数 J 损失函数J 损失函数J 就会取到一个值。
如下图,对于某一个点,存在一个 参 数 t h e t a 参数theta 参数theta,相应的就有一个 损 失 函 数 J 损失函数J 损失函数J。
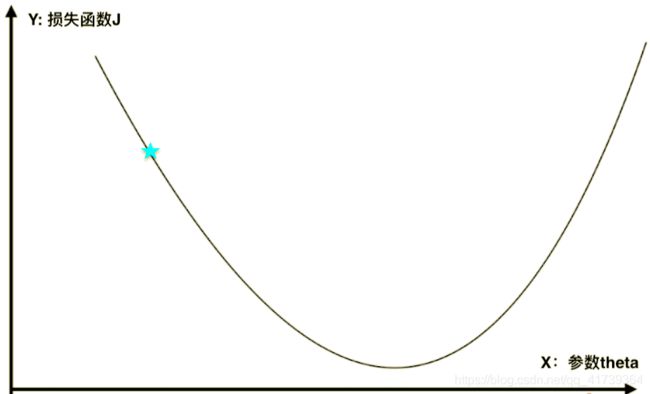
如果蓝点的导数不为零,那么这一点肯定不在一个极值点上 d J d θ \frac{dJ}{d\theta} dθdJ。
- 在直线方程中,导数代表斜率;
- 在曲线方程中,导数代表切线斜率;
- 在这里,导数代表变化比例, θ 单 位 变 化 时 , J 相 应 的 变 化 是 多 少 \theta单位变化时,J相应的变化是多少 θ单位变化时,J相应的变化是多少。
更进一步,导数(梯度)可以代表方向,对应J增大/减小的方向。
因为我们要寻找的是 损 失 函 数 J 损失函数J 损失函数J 的最小值,那就是负方向: − d J d θ -\frac{dJ}{d\theta} −dθdJ。
此外,移动还会有步长: − η d J d θ -\eta\frac{dJ}{d\theta} −ηdθdJ。
移动步长 η \eta η 是一个常数,通常是 0.1 0.1 0.1,这是一个超参数,需要调参得到最佳 η \eta η。
整个过程,每次向负方向移动 η \eta η,再求导数,再移动,不断循环,直到找到最低点。
在我们举的例子里,用的一维函数,直接用导数即可;但在多维函数中,需要对各个方向的分量分别求导,最终得到的方向就是梯度。
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:
一个人被困在山上,需要从山上下来(找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,而后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。而后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。

我们同时可以假设这座山最陡峭的地方是无法通过肉眼立马观察出来的,而是需要一个复杂的工具来测量,同时,这个人此时正好拥有测量出最陡峭方向的能力。所以,此人每走一段距离,都需要一段时间来测量所在位置最陡峭的方向,这是比较耗时的。那么为了在太阳下山之前到达山底,就要尽可能的减少测量方向的次数。这是一个两难的选择,如果测量的频繁,可以保证下山的方向是绝对正确的,但又非常耗时,如果测量的过少,又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率,来确保下山的方向不错误,同时又不至于耗时太多!
就是有一个小问题:

从图中的初始点出发,梯度下降找到的只是局部最优解。
解决方法也很简单:
- 多次运行,随机初始化初始点(初始点也是一个超参数)
假设现在有一张地图,你对这张地图上的地形一无所知,但是如果你报出地图上任何一个位置坐标,系统都能告诉你这个地点的高度是多少。你的任务是在有限的时间内,通过这种问答的试探方法,在地图上找到尽可能高的一座山。你怎么办呢?
最笨的办法是从地图左上角开始一个点一个点的问,可是这样速度太慢了。
-
是随机地选取若干个点,得到每个点的高度,只要时间还有你就不停地问,时间到了就选择你遇到的最高的一点。这个方法的效率也不行,完全靠运气。
-
还有一个办法是从某一点开始,考察这个点临近一米处各个点的高度,选择最高的一点,而后从这个新点出发,再选择它周围最高的一点。这其实就是一个爬山的办法 —— 这个办法能确保你找到最初一点附近的一座山。
-
而最好的办法(梯度下降法),是把随机选点和爬山结合起来。先随机选一些点,找到其中最高的一点,再在这个点附近若干公里的范围内随机选点,又选择其中最高的一点,而后从这点出发爬山。
用这个办法,你未必能发现地图上最高的山,但是一定能在有限的时间内发现一座比较高的山。而如果你一开始的某个点落在了青藏高原上,这个办法可以确保你发现喜马拉雅山。
起始点对梯度下降法是十分重要的,在函数有很多局部最优解的情况下,多次随机选点,也不一定能找到最优解,但一定可以发现更好的解。
import numpy as np
import matplotlib.pyplot as plt
plot_x = np.linspace(-1, 6, 141)
# 头尾 140 个点
plot_y = (plot_x-2.5)**2-1
# 二次曲线(损失函数),目标找到这条曲线最小值
plt.plot(plot_x, plot_y)
plt.show()
# 求损失函数对应的导数,看当前 theta 对应的导数是多少
def dJ(theta):
return 2*(theta-2.5)
# 求损失函数,看当前 theta 对应的损失函数是多少
def J(theta):
return (theta-2.5)**2-1
# 实现梯度下降法
eta = 0.1
theta = 0.0
epsilon = 1e-8
while 1:
gradient = dJ(theta) # 求梯度(一维函数的梯度就是导数)
last_theta = theta
theta = theta - eta * gradient # 梯度 * (-eta),往负的方向走,步长为 eta
if( abs(J(theta) - J(last_theta)) < epsilon ): # 判断是否是最低点(这一次损失函数比上一次小),浮点数运算有精度问题,不能直接判断
break
print(theta)
print(J(theta), J(last_theta))
输出:
2.499891109642585
-0.99999998814289 -0.9999999814732657
我们可视化一下,这个走法:
# 求损失函数对应的导数,看当前 theta 对应的导数是多少
def dJ(theta):
return 2*(theta-2.5)
# 求损失函数,看当前 theta 对应的损失函数是多少
def J(theta):
return (theta-2.5)**2-1
# 实现梯度下降法
eta = 0.1
theta = 0.0
epsilon = 1e-8
theta_history = [theta]
while 1:
gradient = dJ(theta) # 求梯度(一维函数的梯度就是导数)
last_theta = theta
theta = theta - eta * gradient # 梯度 * (-eta),往负的方向走,步长为 eta
theta_history.append(theta)
if( abs(J(theta) - J(last_theta)) < epsilon ): # 判断是否是最低点(这一次损失函数比上一次小),浮点数运算有精度问题,不能直接判断
break
plt.plot(plot_x, J(plot_x))
plt.plot(np.array(theta_history), J(np.array(theta_history)), color='r', marker='+')
plt.show()
输出:

+号是每次的步点,一开始步长大,后面步长就越来越小。虽然公式一直都是乘 eta,而 eta 是不变的常数,但是梯度一开始比较大(比较陡),后面月亮越平缓,步子也就小了。
批量梯度下降法
前置:线性回归(Linear Regression)
-
第一部分:多元线性回归: y = a 1 x 1 + a 2 x 2 + ⋅ ⋅ ⋅ + a n x n + b y=a_{1}x_{1}+a_{2}x_{2}+···+a_{n}x_{n}+b y=a1x1+a2x2+⋅⋅⋅+anxn+b
-
第二部分:为了推导方便,我们构造一个 X 0 i X_{0}^{i} X0i,这个恒等于 1 1 1。
-
第一部分: X b X_{b} Xb 是在 X X X 的基础上,添加了一列 1 ( X 0 i ) 1 (X_{0}^{i}) 1(X0i)。
-
第二部分: y ^ = X i ⋅ θ − > y ^ = X b ⋅ θ \hat{y}=X_{i}·\theta~ -> ~\hat{y}=X_{b}·\theta y^=Xi⋅θ −> y^=Xb⋅θ

-
第一部分:经过变换,就从原损失函数 ∑ i = 1 m ( y i − y ^ i ) 2 \sum\limits_{i=1}^m(y_{i} - \hat{y}_{i})^{2} i=1∑m(yi−y^i)2中推导出了新损失函数 ∑ i = 1 m ( y − X b ⋅ θ ) T ( y − X b ⋅ θ ) \sum\limits_{i=1}^m(y-X_{b}·\theta)^{T}(y-X_{b}·\theta) i=1∑m(y−Xb⋅θ)T(y−Xb⋅θ)。

-
第一部分:推导出来的结果,也称为多元线性回归的正规方程解。
好,看看线性回归里面的梯度下降法。
-
梯度下降的Y轴:多元线性回归的损失函数: J = ∑ i = 1 m ( y i − y ^ i ) 2 J = \sum\limits_{i=1}^m(y_{i} - \hat{y}_{i})^{2} J=i=1∑m(yi−y^i)2。
-
梯度下降的X轴:参数 θ \theta θ,从一个数字 θ \theta θ 变成一组向量 θ \theta θ。
我们的目标:使得损失函数 J = ∑ i = 1 m ( y i − y ^ i ) 2 J = \sum\limits_{i=1}^m(y_{i} - \hat{y}_{i})^{2} J=i=1∑m(yi−y^i)2 尽可能小。
-
y ^ i = θ 0 X 0 i + θ 1 X 1 i + θ 2 X 2 i + ⋅ ⋅ ⋅ + θ n X n i \hat{y}_{i}=\theta_{0}X_{0}^{i}+\theta_{1}X_{1}^{i}+\theta_{2}X_{2}^{i}+···+\theta_{n}X_{n}^{i} y^i=θ0X0i+θ1X1i+θ2X2i+⋅⋅⋅+θnXni (y 的预测值)
-
∑ i = 1 m ( y i − θ 0 X 0 i + θ 1 X 1 i + θ 2 X 2 i + ⋅ ⋅ ⋅ + θ n X n i \sum\limits_{i=1}^m(y_{i} - \theta_{0}X_{0}^{i}+\theta_{1}X_{1}^{i}+\theta_{2}X_{2}^{i}+···+\theta_{n}X_{n}^{i} i=1∑m(yi−θ0X0i+θ1X1i+θ2X2i+⋅⋅⋅+θnXni (代入 y 的预测值)
我们的目标:使得 J = ∑ i = 1 m ( y i − θ 0 X 0 i + θ 1 X 1 i + θ 2 X 2 i + ⋅ ⋅ ⋅ + θ n X n i J = \sum\limits_{i=1}^m(y_{i} - \theta_{0}X_{0}^{i}+\theta_{1}X_{1}^{i}+\theta_{2}X_{2}^{i}+···+\theta_{n}X_{n}^{i} J=i=1∑m(yi−θ0X0i+θ1X1i+θ2X2i+⋅⋅⋅+θnXni 尽可能小。
按照梯度下降法的思路: J = d J d θ J=\frac{dJ}{d\theta} J=dθdJ:

求 向量 θ \theta θ 的 损失函数 J J J 就是对 θ \theta θ 每一个维度的未知量求导。

这种梯度下降法,又称为批量梯度下降法,每一次计算的过程,都需要将信息批量的计算,求和 m m m次。
所以就有一个缺陷,样本量 m m m越大,计算的结果也就越大,这不合理。
因此,我们还需要修改一下公式,去除 样本量 m m m 的影响 — 损失函数除以 样本量 m m m 即可。

这个方法也是多元线性回归中的 均方误差 MSE(Mean Squared Error)。
import numpy as np
np.random.seed(666)
x=2*np.random.random(size=100)
# 添加噪音
y=x*3.+4.+np.random.normal(size=100)
X=x.reshape(-1,1)
# 损失函数
def J(theta, X_b, y):
try:
return np.sum((y-X_b.dot(theta))**2)/len(X_b)
except:
return float('inf')
def dJ(theta, X_b, y):
res=np.empty(len(theta))
res[0]=np.sum(X_b.dot(theta)-y)
for i in range(1,len(theta)):
res[i]=(X_b.dot(theta)-y).dot(X_b[:,i])
# 点乘 5X1点乘 5X1,对应想乘然后加起来(1,2,3)点乘(1,2,3)=1*1+2*2+3*3
return res*2/len(X_b)
def liner_gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
theta=initial_theta
i_iter=0
while i_iter<n_iters:
gradient=dJ(theta,X_b,y)
last_theta=theta
theta=theta-eta*gradient
if(abs(J(theta,X_b,y)-J(last_theta,X_b,y))<epsilon):
break
i_iter+=1
return theta
X_b=np.hstack( [ np.ones((len(X),1)), X ] )
initial_theta=np.zeros(X_b.shape[1])
eta=0.01
theta=liner_gradient_descent(X_b, y, initial_theta,eta)
print(theta)
输出结果:
[4.02145786 3.00706277]
# [截距,系数]
随机梯度下降法
批量梯度下降法,每一次计算的过程,都需要将信息批量的计算,那我们可不可以每次只对其中的一个样本进行计算呢?
- 每次都随机取一个 X i X_{i} Xi,计算出 2 ⋅ ( X b i ) T ⋅ ( X b i θ − y i ) 2·(X^{i}_{b})^{T}·(X_{b}^{i}\theta-y^{i}) 2⋅(Xbi)T⋅(Xbiθ−yi) 的方向。
这个思路就叫做随机梯度下降法。

只是目前在学习速度上还有一个问题,如上图,在最内圈总是在最小值周围徘徊,随机的过程不够好。
我们要设计一个函数,让学习率随循环次数的增多而减少,最简单的方法就是倒数 η = 1 i − i t e r s \eta=\frac{1}{i-iters} η=i−iters1。
不过倒数这种方法也有问题,当循环次数很小时,学习率 η \eta η 下降速度极快。
比如,循环次数从1变到2, η \eta η一下就下降了50%,可循环次数从10000变到20000, η \eta η只是下降了万分之一。
所以,在分母上需要加一个常数,缓解这种情况:
- η = 1 i − i t e r s + b \eta=\frac{1}{i-iters+b} η=i−iters+b1
此外,分子如果固定取 1,可能也达不到理想的效果,分子也取一个常数:
- η = a i − i t e r s + b \eta=\frac{a}{i-iters+b} η=i−iters+ba
import numpy as np
np.random.seed(666)
m = 100
x=2*np.random.random(size=m)
# 添加噪音
y=x*3.+4.+np.random.normal(size=m)
X=x.reshape(-1,1)
def dJ_sgd(theta, X_b_i, y_i):
return X_b_i.T.dot(X_b_i.dot(theta) - y_i) * 2
def sgd(X_b, y, initial_theta, n_iters):
t0 = 5
t1 = 50
def learning_rate(t):
return t0 / (t + t1)
theta = initial_theta
for cur_iter in range(n_iters):
rand_i = np.random.randint(len(X_b))
grandient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
theta = theta - learning_rate(cur_iter) * grandient
return theta
X_b = np.hstack([np.ones((len(X), 1)), X])
initial_theta = np.zeros(X_b.shape[1])
theta = sgd(X_b, y, initial_theta, n_iters=len(X_b)//3)
print(theta)
输出结果:
[3.88215565 3.00499449]
# [截距,系数] , m = 100
对比批量梯度下降法的 [4,3] 也很接近了,随机梯度就是批量梯度的近似,运算速度上更快,适用于精度换时间。
如果要发挥随机梯度的威力,代码中的 m m m需要大数支持,比如m=100变成m=10000,精度变成了:
[3.98882831 3.03079223]
# m = 10000
scikit-learn中的随机梯度下降法
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston = datasets.load_boston()
X, y = boston.data, boston.target
X = X[y < 50.0]
y = y[y < 50.0]
X_train, X_test, y_train, y_test=train_test_split(X, y)
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor()
sgd_reg.fit(X_train_standard, y_train)
ans = sgd_reg.score(X_test_standard, y_test)
print(ans)
小批量梯度下降法
除了批量梯度下降(每次都要对所有样本看一遍)、随机梯度下降(每次只要看一个样本,速度快,但不稳定可能会向反方向前进)。
所以,我们就想取俩者的精华,不用每次看全部,也不只看一个,看一部分不是更好吗!
这就是小批量梯度下降法。
def fit_sb_gd(self, X, y, n_iters=5, s=10):
def dJ(theta, X_b_s, y_i_s):
return X_b_s.T.dot(X_b_s.dot(theta) - y_i_s) * 2 / len(X_b_s)
def sb_gd(initial_theta, X_b, y, n_iters, t0=5, t1=50):
def learnint_rate(t):
return t0 / (t + t1)
theta = initial_theta
m = len(X_b)
for i in range(int(n_iters)):
rand_index = np.random.permutation(m)
X_rand = X_b[rand_index,:]
y_rand = y[rand_index]
for j in range(0, m, s):
max_index = np.min((j+s, m))
gradient = dJ(theta, X_rand[j:max_index], y_rand[j:max_index])
theta = theta - learnint_rate(i * m + (j+max_index) // 2) * gradient
return theta
X_b = np.hstack([ np.ones((len(X), 1)) , X])
initial_theta = np.zeros(X_b.shape[1])
self._theta = sb_gd(initial_theta, X_b, y, n_iters)
self.coef_ = self._theta[1:]
self.inteceptor_ = self._theta[0]
return self




