opencv与计算机视觉
opencv与计算机视觉
计算机视觉:是一门研究如何使机器“看”的科学,更进一步的说,就是是指用摄影机和电脑代替人眼对目标进行识别、跟踪和测量等机器视觉,并进一步做图形处理,使电脑处理成为更适合人眼观察或传送给仪器检测的图像。(百度百科)
opencv:简单的说就是为你提供一个处理图片和视频的框架,可以使用opencv或者自己的算法,不用担心分配和释放图片的内存,所以opencv最强大的地方在于它强大的内存管理和自身的架构。
用计算机对图像进行处理的技术–图像处理
常用方法
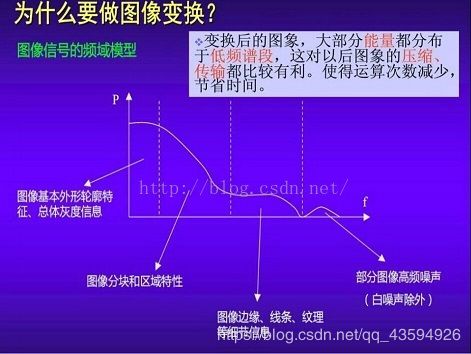
(1)图像变换:由于图像阵列很大,直接在空间域中进行处理,涉及计算量很大。因此,往往采用各种图像变换的方法,如傅立叶变换 离散余弦变换(高斯模糊)。
(2 )图像编码压缩:图像编码压缩技术可减少描述图像的数据量(即比特数),以便节省图像传输、处理时间和减少所占用的存储器容量。
(3)图像增强和复原:图像增强和复原的目的是为了提高图像的质量,如去除噪声,提高图像的清晰度等。图像增强不考虑图像降质的原因,突出图像中所感兴趣的部分。如强化图像高频分量,可使图像中物体轮廓清晰,细节明显;如强化低频分量可减少图像中噪声影响。图像复原要求对图像降质的原因有一定的了解,一般讲应根据降质过程建立“降质模型”,再采用某种滤波方法,恢复或重建原来的图像。
常用方法:灰度增强(直方图均衡化),线性滤波器。
(4)图像分割:图像分割是数字图像处理中的关键技术之一。图像分割是将图像中有意义的特征部分提取出来,其有意义的特征有图像中的边缘、区域等。
图像边缘处理方法:边缘检测
(5)图像描述
(6)图像分类(识别):图像分类(识别)属于模式识别的范畴,其主要内容是图像经过某些预处理(增强、复原、压缩)后,进行图像分割和特征提取,从而进行判决分类。图像分类常采用经典的模式识别方法,有统计模式分类和句法(结构)模式分类。
矩阵变换 傅里叶变换与高斯模糊
1.傅里叶变换

1.1 能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅立叶变换具有多种不同的变体形式,如连续傅立叶变换和离散傅立叶变换。傅立叶变换是一种分析信号的方法,它可分析信号的成分可用这些成分合成信号
1.2 性质:线性性质 尺度变换性质 对偶性 平移性质 微分关系 时域卷积定理 频域卷积定理
2.高斯模糊
2.1所谓高斯模糊,就是指一个图像与二维高斯分布的概率密度函数做卷积。它的效果如下:

高斯模糊常常用来模拟人眼中的物体变远、变快的效果。在照片处理中,我们常常将背景施以高斯模糊,使得背景仿佛变远了,从而突出前景的人物或物体。高斯模糊对于图像来说就是一个低通滤波器。
2.2机理:高斯模糊是一种图像模糊滤波器,它用正态分布计算图像中每个像素的变换。N维空间正态分布方程为
其中r是模糊半径,σ是正态分布的标准偏差。在二维空间中,这个公式生成的曲面的等高线是从中心开始呈正态分布的同心圆。分布不为零的像素组成的卷积矩阵与原始图像做变换。每个像素的值都是周围相邻像素值的加权平均。原始像素的值有最大的高斯分布值,所以有最大的权重,相邻像素随着距离原始像素越来越远,其权重也越来越小。这样进行模糊处理比其它的均衡模糊滤波器更高地保留了边缘效果。
2.3应用:图像卷积滤波
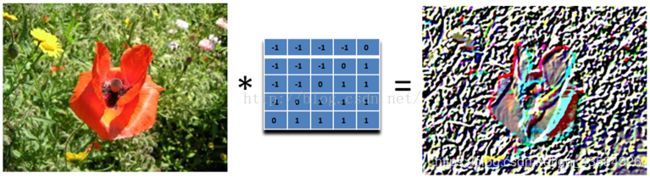
它是图像处理最基本的方法,可以产生不同的效果。比如

可以看到原图像经过二维的图像滤波矩阵(卷积核)处理后可以变换成为另一个图像,对于原图像的每一个像素点来说,计算它的领域之内的像素和滤波矩阵对应元素的乘积,相加得到的值作为当前中心像素位置的值,这样就完成了滤波的功能。
对于滤波器的要求
① 滤波器的大小应该是奇数,这样它才有一个中心,例如3x3,5x5或者7x7。有中心了,也有了半径的称呼,例如5x5大小的核的半径就是2。
② 滤波器矩阵所有的元素之和应该要等于1,这是为了保证滤波前后图像的亮度保持不变。当然了,这不是硬性要求了。
③ 如果滤波器矩阵所有元素之和大于1,那么滤波后的图像就会比原图像更亮,反之,如果小于1,那么得到的图像就会变暗。如果和为0,图像不会变黑,但也会非常暗。
④ 对于滤波后的结构,可能会出现负数或者大于255的数值。对这种情况,我们将他们直接截断到0和255之间即可。对于负数,也可以取绝对值。
2.4卷积核的一些用法
2.4.1 空卷积核
滤波后得到的图和原图是一样的。因为只有中心点的值是1。邻域点的权值都是0,对滤波后的取值没有任何影响。
图像的锐化和边缘检测很像,首先找到边缘,然后把边缘加到原来的图像上面,这样就强化了图像的边缘,使图像看起来更加锐利了。这两者操作统一起来就是锐化滤波器了,也就是在边缘检测滤波器的基础上,再在中心的位置加1,这样滤波后的图像就会和原始的图像具有同样的亮度了,但是会更加锐利。

我们把核加大,就可以得到更加精细的锐化效果
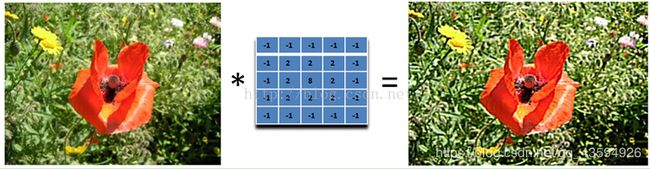
另外,下面的滤波器会更强调边缘
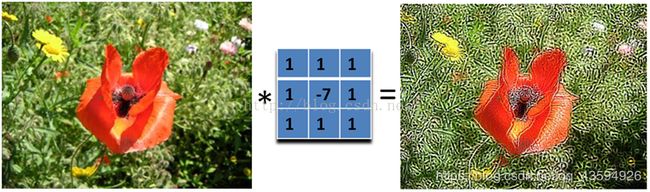
2.4.3浮雕
浮雕滤波器可以给图像一种3D阴影的效果。只要将中心一边的像素减去另一边的像素就可以了。这时候,像素值有可能是负数,我们将负数当成阴影,将正数当成光,然后我们对结果图像加上128的偏移。这时候,图像大部分就变成灰色了。
下面是45度的浮雕滤波器
我们可以将当前像素和它的四邻域的像素一起取平均,然后再除以5,或者直接在滤波器的5个地方取0.2的值即可
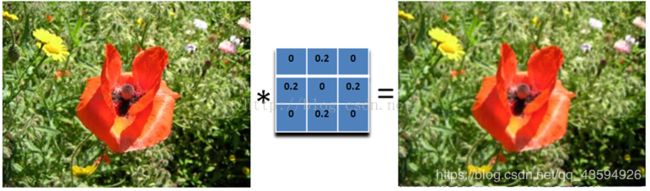
可以看到,这个模糊还是比较温柔的,我们可以把滤波器变大,这样就会变得粗暴了:注意要将和再除以13.

可以看到均值模糊也可以做到让图片模糊,但是它的模糊不是很平滑,不平滑主要在于距离中心点很远的点与距离中心点很近的所带的权重值相同,产生的模糊效果一样,而想要做到平滑,让权重值跟随中心点位置距离不同而不同,则可以利用正态分布(中间大,两端小)这个特点来实现。
高斯模糊
有了前面的知识,我们知道如果要想实现高斯模糊的特点,则需要通过构建对应的权重矩阵来进行滤波。
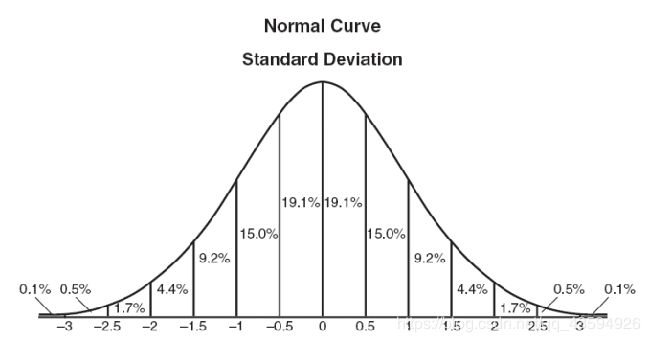
3.1正态分布
计算平均值的时候,我们只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值。正态分布显然是一种可取的权重分配模式。
3.2 高斯函数–用来描述正态分布
上面的正态分布是一维的,而对于图像是二维的,所以我们需要二维的正态分布。
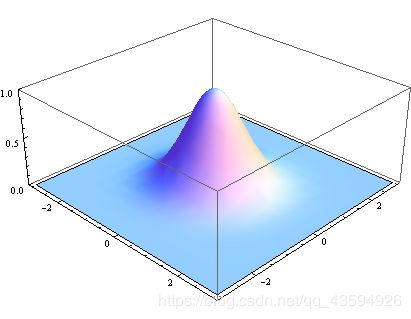
正态分布的密度函数叫做"高斯函数"(Gaussian function)。它的一维形式是:
其中,μ是x的均值,σ是x的方差。因为计算平均值的时候,中心点就是原点,所以μ等于0。
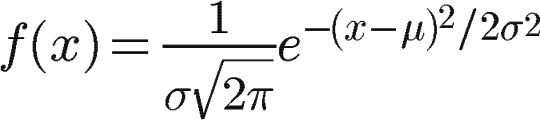
根据一维高斯函数,可以推导二维高斯函数:
3.3获取权重矩阵
假设中心点坐标为(0,0)

为了计算权重矩阵,需要设定σ的值。假定σ=1.5,则模糊半径为1的权重矩阵如下:
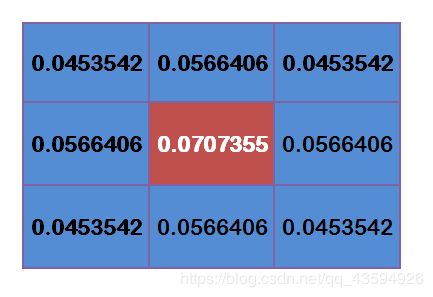
这9个点的权重总和等于0.4787147,如果只计算这9个点的加权平均,还必须让它们的权重之和等于1,因此上面9个值还要分别除以0.4787147,得到最终的权重矩阵。
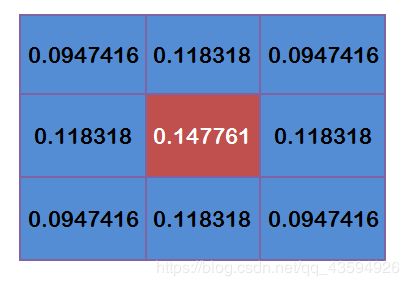
除以总值这个过程也叫做”归一问题“
目的是让滤镜的权重总值等于1。否则的话,使用总值大于1的滤镜会让图像偏亮,小于1的滤镜会让图像偏暗。
接下来计算高斯模糊的值就好啦。
代码
导入头文件
#include 调用摄像头
VideoCapture video(0);
while (true)
{
Mat frame;//视频的每一帧
video >> frame; //将视频写入每一帧
cvtColor(frame,frame,COLOR_RGB2GRAY);
cvNamedWindow("frame", WINDOW_AUTOSIZE);
imshow("frame",frame);
waitKey(30);
}
高斯模糊实现
Mat srcImage = imread("D:\\Desktop\\lena.jpg", 1); //读取图片
cvtColor(srcImage, srcImage,COLOR_BGR2GRAY); //转为灰度图像
namedWindow("srcImage", WINDOW_AUTOSIZE); //新建窗口
imshow("srcImage", srcImage); //显示图像
//waitKey(0); //图像显示为一帧
//由于中型差分的原因,输出图像比原始图象少了两列
Mat dImage = Mat(srcImage.rows,srcImage.cols - 2,CV_8UC1);
//循环遍历整个图像
for (int i = 0; i < srcImage.rows; i++)
{
for (int j = 1; j < srcImage.cols - 1; j++)
{
//对整型数据类型进行运算,进行中型差分
dImage.at<uchar>(i, j - 1) = srcImage.at<uchar>(i, j + 1) - srcImage.at<uchar>(i, j - 1);
}
}
namedWindow("dImage", WINDOW_AUTOSIZE); //处理后图像窗口
imshow("dImage", dImage); //显示处理后的图像
waitKey(0); //图像显示为一帧
Mat srcImage = imread("D:\\Desktop\\lena.jpg", 1); //读取图片
cvtColor(srcImage, srcImage, COLOR_BGR2GRAY); //转为灰度图像
namedWindow("srcImage", WINDOW_AUTOSIZE); //新建窗口
imshow("srcImage", srcImage); //显示图像
/*高斯模糊*/
//5×5卷积模板
Mat model = Mat(5, 5, CV_64FC1);
double sigma = 80; //超参数,根据经验所得
for (int i = - 2; i <= 2 ; i++) //进行遍历
{
for (int j = -2; j <= 2; j++)
{
//正态分布
model.at<double>(i + 2, j + 2) =
exp(-(i * i + j * j) / (2 * sigma * sigma)) /
(2 * PI * sigma * sigma);
}
}
//归一化
double gaussSum = 0;
gaussSum = sum(model).val[0]; //卷积核 求和
for (int i = 0; i < model.rows; i++)
{
for (int j = 0; j < model.cols; j++)
{
model.at<double>(i, j) = model.at<double>(i, j)
/ gaussSum;
}
}
Mat dst = Mat(srcImage.rows - 4,srcImage.cols - 4,CV_8UC1);
//对整个图片进行遍历卷积
for (int i = 2; i < srcImage.rows - 2; i++)
{
for (int j = 2; j < srcImage.cols - 2; j++)
{
double sum = 0; //求和目标值
for (int m = 0; m < model.rows; m++)
{
for (int n = 0; n < model.cols; n++)
{
sum += (double)srcImage.at<uchar>(i + m - 2, j + n - 2) *
model.at<double>(m,n); //对整个卷积核进行卷积
}
}
dst.at<uchar>(i - 2, j - 2) = (uchar)sum; //结果赋值到dst图像当中
}
}
namedWindow("gaussBlur", WINDOW_AUTOSIZE);
imshow("gaussBlur", dst);
waitKey(0); //图像显示为一帧调用高斯模糊库函数
Mat dst = srcImage.clone();
//一行代码高斯模糊
GaussianBlur(srcImage, dst, Size(17, 17), 180);
namedWindow("gaussBlur", WINDOW_AUTOSIZE);
imshow("gaussBlur", dst);
waitKey(0); //图像显示为一帧运行结果
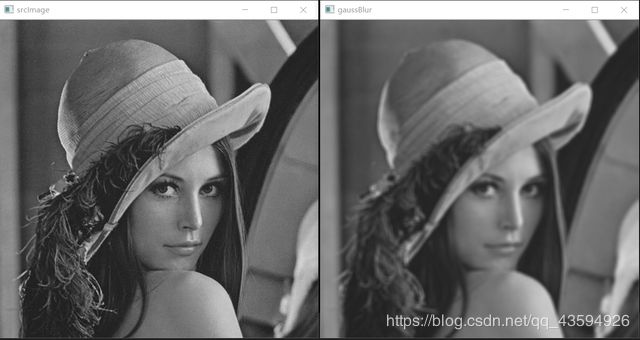
参考
[高斯模糊(https://www.cnblogs.com/invisible2/p/9177018.html)
[(https://imlogm.github.io/图像处理/image-fft/)
[(http://www.cvvision.cn/8907.html)
[https://www.jianshu.com/p/191d1e21f7ed?tdsourcetag=s_pcqq_aiomsg)
百度百科
培训感受
感觉学长们很厉害,可以把很多东西深入浅出的讲解,让我们这些小白对图像处理方面有一些全新的认识和了解,给我们提供了又一个新的方向,但是我知道,师傅领进门修行在个人,希望自己做好手边的每一件事情,谢谢各位前辈的指点(●ˇ∀ˇ●)
要努力( •̀ ω •́ )