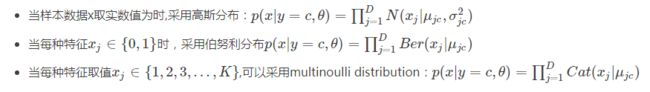分类问题:概率生成模型
1、分类问题及其解决方法
1)首先,什么是分类问题
2)接着,分类问题该如何解决呢
2、建立概率生成模型的步骤(以朴素贝叶斯分类器为例)
step1:求先验概率
step2:确定数据属于哪一个分布,用最大似然估计出分布函数的参数
step3:求出后验概率
3、生成模型解决分类问题的总结以及逻辑回归方法(判别模型)的引出
1、 分类问题及解决方法
1) 首先,什么是分类问题
input 为一系列参数或信息,output 为一个类别
2) 接着,分类问题如何解决
课程以神奇宝贝的系别分类为例,判断一直精灵属于 水系 还是 普通系
对于二分类问题,定义一个function,当函数值大于0就划分为类别1,否则就为类别2.
Loss function(损失函数)定义为在测试数据上误分类的次数。
Ideal Alternatives(理想方案)
问题在于这个 function 是怎样的?
实际上,它可以是一个概率模型 P(C1| X),当 P(C1| X)>0.5,就说明x 是class 1的。
下面需要了解这个模型是如何生成的
2、建立概率生成模型的步骤(以朴素贝叶斯分类器为例)
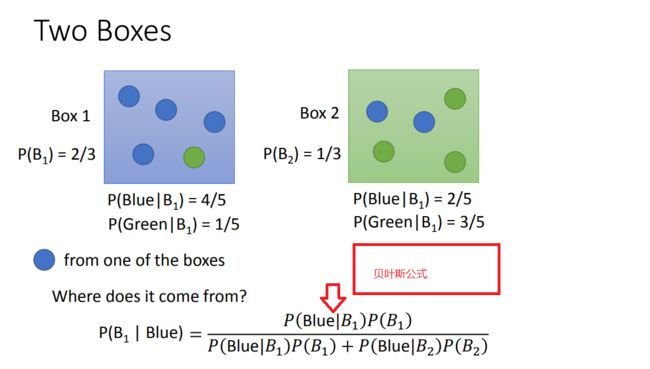
首先,举个栗子引出贝叶斯,有两个盒子,每个盒子里面各有一定数量的蓝球和绿球,现在我取到一个蓝球,
问这个蓝球是来自于第一个盒子的概率。这就要用到贝叶斯公式(由果求因)
然后,把这个公式应用于我们的分类问题:假设有两个类别(水系和普通系),每个类别有不同的精灵,
现在我抓到一个精灵,那么它是属于水系和普通系的概率分别是多少。
进一步,在开始做生成模型之前,掌握以下概念
先验概率:统计历史上的经验和数据得到的概率,比如我们出门的时候,堵车的概率就是先验概率 。
这里是P(c1)——样本中的精灵是水系的概率
P(x|c1):有因求果的条件概率 ,也就是P(堵车|交通事故)。
这里是指水系中是比卡丘的概率
似然估计:好像(交通事故会引起堵车)是正确的。
这里要估计P(x|c1)
后验概率:有果求因,也就是P(交通事故|堵车)。
这里指抓到的比卡丘是水系的概率
stpe 1:求先验概率
假设编号小于400的精灵作为 training data ,其中79只水系,61只普通系。
stpe 2:选择概率分布函数,用最大似然估计出分布函数得到参数
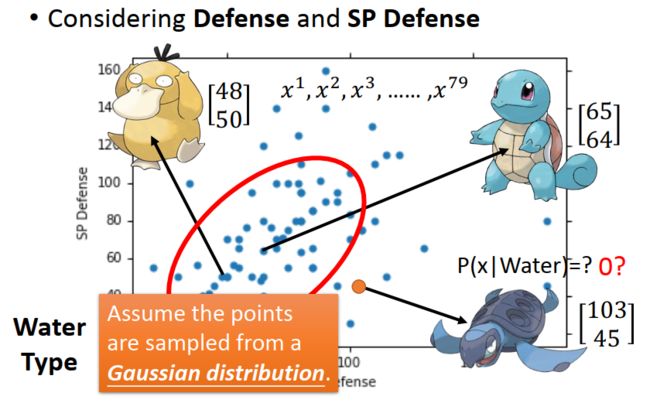
1、首先,我们目标是求水系样本中的79个精灵中,抓到其中一种精灵的概率(P(x|c1)),那么这个概率应该是跟精灵的属性有关的。
这里我们选择两种属性讨论,此时数据中(x,水系)中的x应该是一个向量(【x1,x2】,水系)
以Defense 和 SP Defense 为例, x=[a, b]T
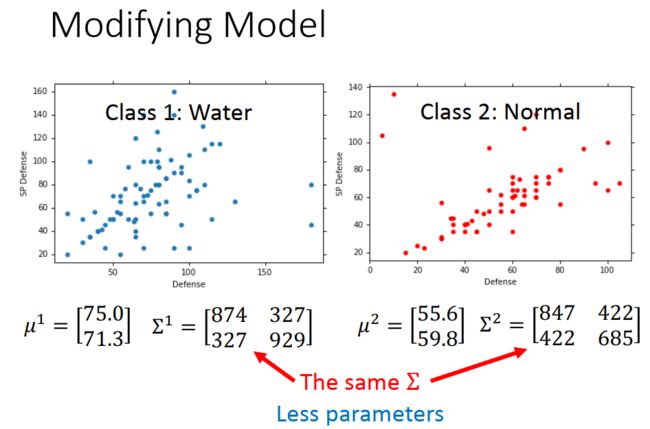
2、然后,这里选择高斯分布(二维):也就是说在水系样本中的79个精灵中,抓到其中一种精灵的概率(P(x | c1))呈高斯分布。
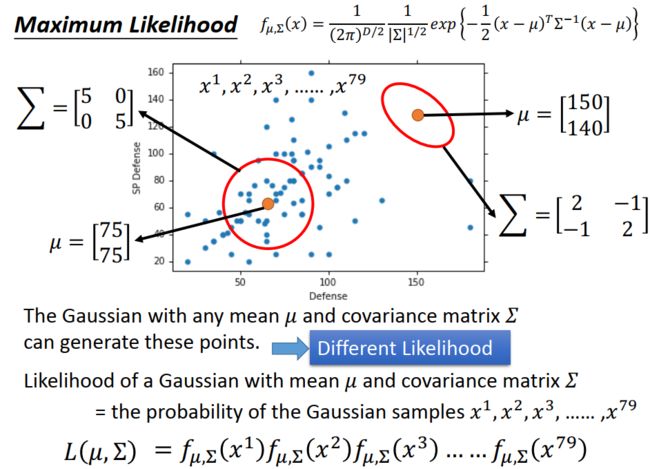
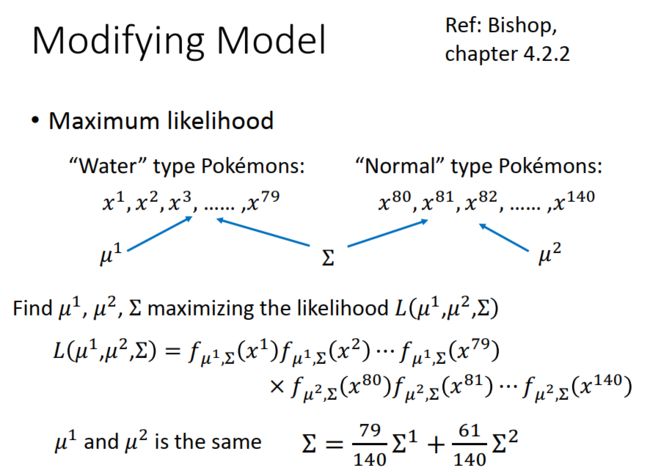
3、接着,用最大似然估计法算出分布函数的参数
似然函数:x1,x2...x79同时出现的概率函数。
最大似然估计:使似然函数最大时的参数估计。
4、同理,我们估计出了水系和普通系的概率分布函数的参数(也就是求出了P(x|c1)、P(x|c2))
Step 3:求后验概率
结果分析:
改进一下:
改进后结果:
3、生成模型解决分类问题的总结以及逻辑回归方法(判别模型)的引出
1) 总结,如何解决分类问题
2)逻辑回归方法(判别模型)的引出