Matlab对语音信号做fft及对语音信号进行分帧加窗

本文主要读取语音信号，画出语音波形，并对语音信号进行fft变换，画出频谱图。再对原语音信号进行分帧，并使用了三种窗函数（矩形窗，海宁窗，海明窗）对其中的一帧进行加窗，查看结果。

• 注：本文所用的matlab版本为matlab 2017a
  首先读取音频文件：

[x1,fs]=audioread('lantian.wav');  %读取音频文件lantian.wav,fs返回采样频率,x1为读取的语音信号

返回语音信号的采样频率，总的采样点数，语音时长等信息：

info=audioinfo('lantian.wav') 

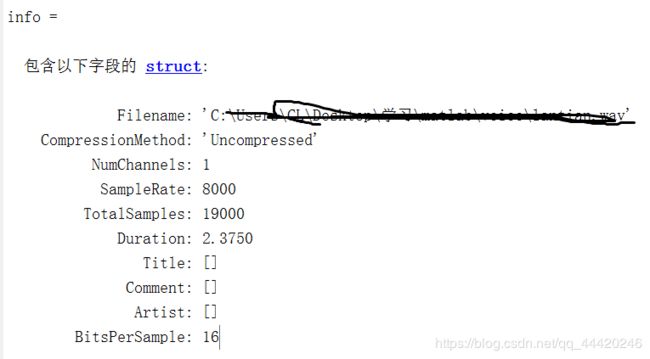
可以看到，该语音采样频率为8000，语音总的采样点数为19000，语音时长为2.375秒。
矩形窗函数：

boxcar(n)  %调用格式：w=boxcar(n)，根据长度 n 产生一个矩形窗 w

海宁窗函数：

hanning(n)  %调用格式：w=hanning(n)，根据长度 n 产生一个汉宁窗 w

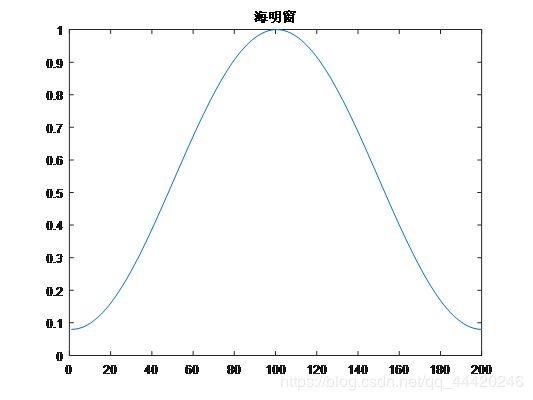
海明窗函数：

hamming(n)  %调用格式：w=hamming(n)，根据长度 n 产生一个海明窗 w

画语音信号波形图：

figure()
subplot(211);
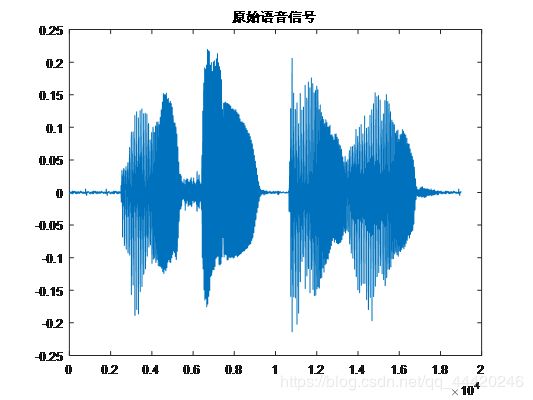
plot(x1);
title('原始语音信号');

波形图如下：

对语音信号进行fft变换：

---

FFT物理意义如下：
一个模拟信号,经ADC采样后，就变成了数字信号，采样频率要大于信号频率的两倍，采样得到的数字信号，就可以做FFT变换了。N个采样点，经过FFT之后，就可得到N个点的FFT结果。为了方便进行FFT运算，通常N取2的整数次方。
假设采样频率为Fs,信号频率为F,采样点数为N。那么FFT之后记过就是一个为N点的复数。每个点就对应有一个频率点。这个点的模值，就是该频率值下的幅度特性。
假设原始信号的峰值为A,它跟原始信号的幅度的关系为, FFT的结果的每个点(除第-一个点直流分量之外)的模值就是A的N/2倍。而第一个点就是直流分量，它的模值就是直流分量的N倍。而每个点的相位，就是该频率下的信号的相位。
FFT运算后第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点（实际上这个点是不存在的，这里是假设的第N+1个点，也可以看做是将第一个点分做两半，另一半移到最后）则表示采样频率Fs，这中间被N-1个点平均分成N等份，每个点的频率依次增加。例如某点n所表示的频率为:Fn=(n-1)*Fs/N。
由上边的公式可以看出，Fn所能分辨到频率为Fs/N,如果采样频率Fs为1024 Hz, 采样点数为1024点,则可以分辨到1 Hz。1024 Hz 的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT,则结果可以分析到1 Hz, 如果采样2秒时间的信号并做FFT,则结果可以分析到0.5 Hz。 如果要提高频率分辨力，则必须增加采样点数，也即采样时间。

---

y1=fft(x1,256);   %对语音信号进行256点fft变换

本文调用了voicebox包中的enframe函数进行分帧处理，但matlab中不自带voicebox包。对于如何安装voicebox包，请参考下面博客：
在MATLAB中添加语音处理工具箱（voicebox）

对语音信号进行分帧：

x2=enframe(x1,200,100);%调用分帧函数enframe,x1为语音信号，200为帧长，100为语音帧移时重叠部分的长度

对语音信号进行分帧，再加不同的窗函数：

x3=enframe(x1,boxcar(200),100);  %每两百个点分为一帧，再加矩形窗
x4=enframe(x1,hanning(200),100);  %每两百个点分为一帧，再加加海宁窗
x5=enframe(x1,hamming(200),100);%每两百个点分为一帧，再加海明窗

完整的代码如下：

clc;
clear;
close all;
[x1,fs]=audioread('lantian.wav');  %读取音频文件lantian.wav
info=audioinfo('lantian.wav') 
figure()
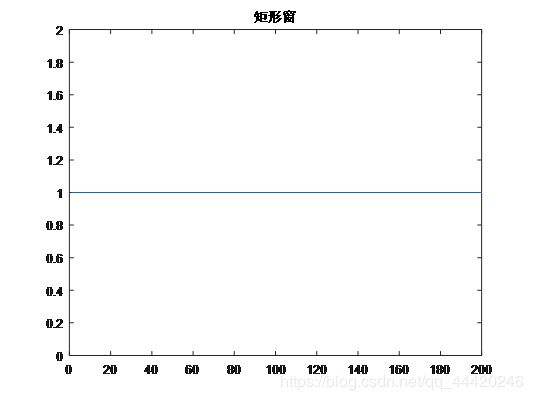
plot(boxcar(200))  %画矩形窗波形
title('矩形窗');
figure()
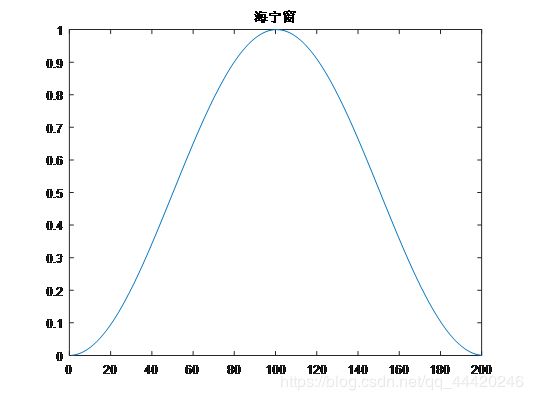
plot(hanning(200))  %画海宁窗波形
title('海宁窗');
figure()
plot(hamming(200))  %画海明窗波形
title('海明窗');
y1=fft(x1,256);   %对语音信号进行256点fft变换
figure()
subplot(211);
plot(x1);
title('原始语音信号');
subplot(212);
plot(abs(y1(1:256)));
title('原始语音信号FFT频谱');
x2=enframe(x1,200,100);%分帧
figure();%画图
subplot(221);
plot(x2(50,:))   %画第50帧波形
title('语音信号第50帧波形');
x3=enframe(x1,boxcar(200),100);%每两百个点分为一帧，再加矩形窗
subplot(222);
plot(x3(50,:))  %画第50帧波形
title('语音信号加矩形窗后第50帧波形');
x4=enframe(x1,hanning(200),100);%每两百个点分为一帧，再加加海宁窗
subplot(223);
plot(x4(50,:))   %画第50帧波形
title('语音信号加海宁窗后第50帧波形');
x5=enframe(x1,hamming(200),100);%每两百个点分为一帧，再加海明窗
subplot(224);
plot(x5(50,:))   %画第50帧波形
title('语音信号加海明窗后第50帧波形');

结果：
矩形窗：

海宁窗：

海明窗：

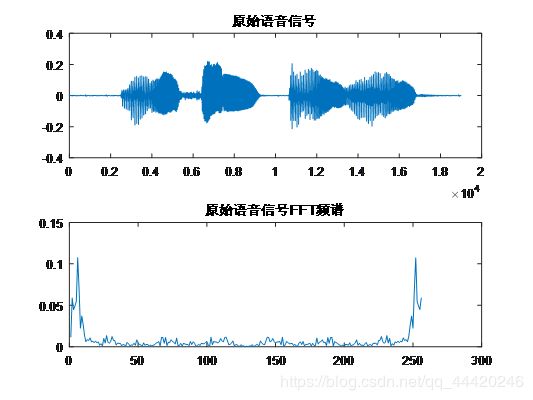
原始语音信号和语音信号的fft变换频谱图：

这是第50帧信号波形，语音信号直接分帧和对语音信号加不同窗函数的对比：

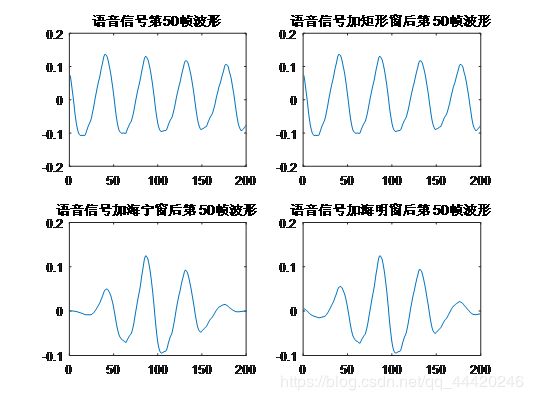
可以发现，对语音信号加矩形窗之后和不加窗的波形几乎一样。但加窗海宁窗和海明窗后结果和不加窗结果不一样，明显两边的波形幅度降低了，中间不变，这是因为海宁窗和海明窗因为边缘有一个下降带，对高于这个值的波形就截断掉了。海宁窗和海明窗效果几乎一样。