完全重建QMF滤波器组的理解

（1）多抽样率技术
实现一个信道中的多路通信完全重建。而QMF滤波器组在对信号进行抽取后，可以根据每个子带的不同特征分别进行处理，而插值和合成环节又能消除信号失真的各种因素，有很突出的优点
（2）以两通道为例，一个两通道正交镜像滤波器组如图，在分析滤波器组一侧，输入信号（设为宽带信号）被分成K个子频带信号（窄带信号），通过抽取可降低采样率；在综合滤波器一侧，通过零值内插和带通滤波可以重建原来的信号

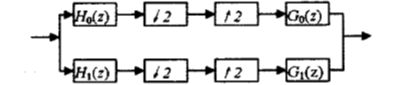
对于一个给定的信号，经过分析滤波器后，再进行抽取、编码、传输，可以通过零值内插、综合滤波器滤波、求和运算得到恢复和重建。但是重建后的信号并不能与原始信号完全相同，两者之间存在着误差，主要包括：
1.混叠失真。由抽取和内插产生的混叠和镜像带来的误差，导致分析滤波器组和综合滤波器组的频带不能完全分开；
2.幅度失真。由于分析和综合滤波器组的频带在通带内不是全通函数，其幅频特性波纹产生的误差；
3.相位失真。由滤波器相频特性的非线性所产生的误差；
4.量化失真。由编、解码产生的误差，与量化噪声相似，这类误差无法完全消除，只能设法减小
（3）解决方法
1.用FIR QMF滤波器组，去除相位失真的前提下，尽可能的减小幅度失真，近似实现完全重建；
2.用IIR QMF滤波器组，去除幅度失真，不考虑相位失真，近似实现完全重建；
3.修正QMF滤波器H0（-z）=H1（z）的关系，去考虑其他更合理的形式，从而实现完全重建
（4）matlab实现简述
完全重建QMFB需要找到合适的N和w，分别依次固定w与N，最终找到重建效果最好的参数值，选取各滤波器的阶数N=41，滤波器h0通带截止频率w=0.43。

matlab代码实现：

clc;
clear;
close all;
N=41;
w=0.43;
[h0,h1,g0,g1]=firpr2chfb(N,w);
[H1z,w]=freqz(h0,1,512);
H1_abs=abs(H1z);H1_db=20*log10(H1_abs);
[H2z,w]=freqz(h1,1,512);
H2_abs=abs(H2z);H2_db=20*log10(H2_abs);
%滤波器h0和h1的幅度响应
figure(1); 
plot(w/pi,H1_db,'-',w/pi,H2_db,'--'); 
axis([0,1,-100,10]); 
grid 
xlabel('\omega/\pi');ylabel('幅度,dB'); 
sum1=H1_abs.*H1_abs+H2_abs.*H2_abs; 
d=10*log10(sum1);
%幅度响应关系误差
figure(2) 
plot(w/pi,d);grid; 
xlabel('\omega/\pi');ylabel('误差,dB'); 
axis([0,1,-0.04,0.04]); 
%%%%%%%%%%%%%x1(n)%%%%%%%%%%%%%%%%%%%%%
x=zeros(1,500);
x(2)=1;x(3)=1;
x(6)=2;x(7)=2;x(8)=2;
x(17)=1.5;x(18)=1.5;x(19)=1.5;
x(24)=1;x(25)=1;
x(33)=3;x(34)=3;x(35)=3;
%%%%%%%%%%%%%%x2(n)%%%%%%%%%%%%%%%%%%%%
x=zeros(1,500);
x(1)=1;x(2)=1;x(3)=1;
x(9)=2;x(10)=2;x(11)=2;
x(16)=3;x(17)=3;x(18)=3;
x(24)=4;x(25)=4;x(26)=4;
x(33)=3;x(34)=3;x(35)=3;
x(41)=2;x(42)=2;x(43)=2;
x(49)=1;x(50)=1;x(51)=1;
%%%%%%%%%%%%%%x3(n)%%%%%%%%%%%%%%%%%%%%
n=1:500;
T=0.2;
x=sin(n*T);
hlp=mfilt.firdecim(2,h0);
hhp=mfilt.firdecim(2,h1);
glp=mfilt.firinterp(2,g0);
ghp=mfilt.firinterp(2,g1);
x0=filter(hlp,x);
x0=filter(glp,x0);
x1=filter(hhp,x);
x1=filter(ghp,x1);
xidle=x0+x1;
xshift=[zeros(1,N) x(1:end-N)];
e=xidle-xshift;
mes=sum(abs(e).^2)/length(e);
fvtool(h0)
%输入信号
figure(4);
plot(x);
%理想输出信号与重建输出信号
figure(5);
axis([0,500,-1,1]); 
plot(xshift,'r');hold on;
plot(xidle,'-');
axis([0,600,-1.1,1.1]);
%理想输出信号与重建输出信号的偏差
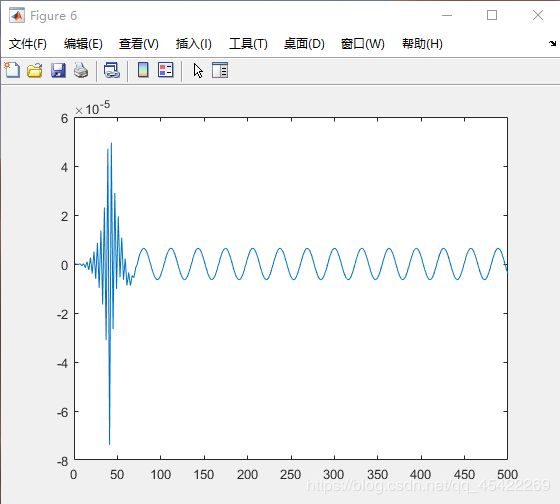
figure(6);
plot(xshift-xidle);

相关结果：
figure1，滤波器H0和滤波器H1的幅度响应

figure2，两者的幅度响应的差值

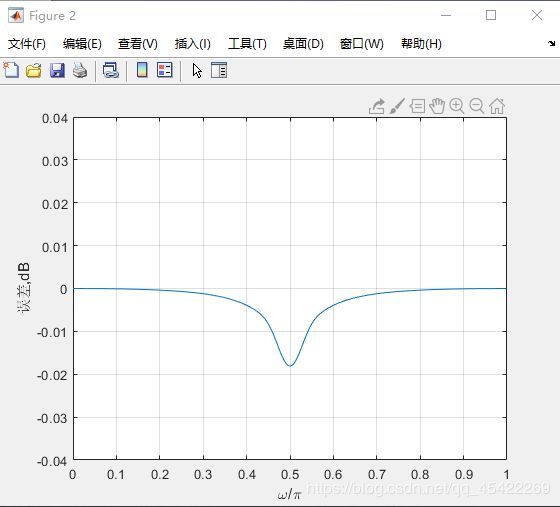
figure3，h0的频率响应

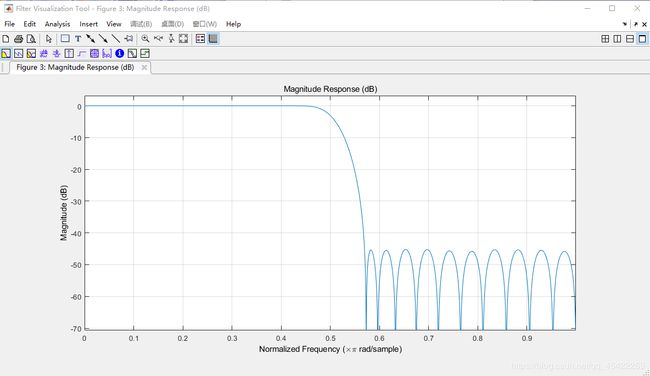
figure4,原信号

fugure5,重建信号

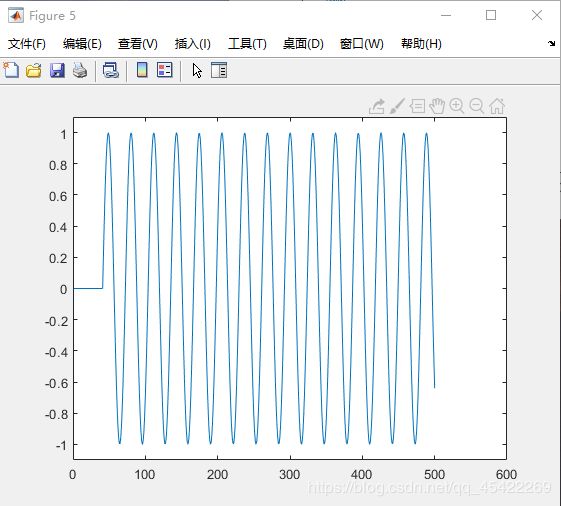
figure6,重建信号与原信号插值差值