acm新手小白必看系列之（6）——gcd与lcm精讲及例题（求最大公约数与最小公倍数）

acm新手小白必看系列之（6）——gcd与lcm精讲及例题

事前须知

• % 求余符号；
• | 整除符号，a|b，表示a能整除b，即b=k*a（k为常数），或b%a==0；
• ≡ 同余符号，a≡b（mod c）为一个同余式，表示a%c=b%c；
• 取模运算的运算规则
  (a + b) % p = (a % p + b % p) % p
  (a - b) % p = (a % p - b % p) % p
  (a * b) % p = (a % p * b % p) % p
  a ^ b % p = ((a % p)^b) % p
  求最大公约数的方法：
  1.辗转相除法（欧几里得算法）
  2.辗转相减法（更相减损术）
  3.素因子分解法
• （1）欧几里得算法又叫辗转相除法,用来求得两个数的最大公约数,记作gcd(a,b)
  怎么用程序实现欧几里得算法？
  实际上我们可以写两种形式的辗转相除：递归和非递归。
• 非递归

int gcd(int a, int b)
{
    while(r)
    {
        a=b;
        b=r;
        r=a%b;
    }
    return b;
}

• 递归（这个常用，如果你会c++就还有个更常用的）

int gcd(int a,int b)
{
    return  b?gcd(b,a%b):a;//啥意思呢？
}

• 讲解一下这个 （ ？：）

三目运算符，即有三个操作数，可以实现if else的功能
一般形式为 表达式1？表达式2：表达式3
例如
if（a>b）
max=a；
else
max=b；
可以用表达式写为
max=（a>b)?a:b;
语义是如果a>b为真，则把a赋予max，否则把b赋予max。
会了吧~翻译一下这个 b?gcd(b,a%b):a

• （2）更相减损术更相减损术和辗转相除法的主要区别在于前者所使用的运算是“减”，后者是“除”。从算法思想上看，两者并没有本质上的区别，但是在计算过程中，如果遇到一个数很大，另一个数比较小的情况，可能要进行很多次减法才能达到一次除法的效果，从而使得算法的时间复杂度退化为O(N)，其中N是原先的两个数中较大的一个。相比之下，辗转相除法的时间复杂度稳定于O(logN)。
  除此之外，相减的算法对于0和负数要特殊拿出来判断，否则会死循环。

1

int gcd(int x, int y)
{
    while(x!=y)
    {
        if(x>y)
            x-=y;
        else
            y-=x;
    }
    return x;
}

2

int gcd(int x,int y)
{
    if(x==y)
        return x;
    return x>y?gcd(x-y,y):gcd(y-x,x);
}

然而还有一个c++里可以调用的函数
__gcd(a,b)
所以懒得打代码就直接用这个吧
（3）素因子分解法
素因子就是素数因子，质数因子
素因子分解法，先要把两个数a,b分解转化成

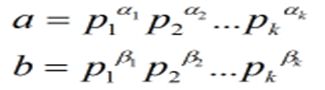
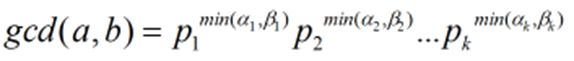
其中p1,p2...pn都为素数；
素因子分解法求最小公倍数&最大公约数；
a=(p1^a1)*(p2^a2)*(p3^a3)…(pm^am),
b=(p1^b1)*(p2^b2)*(p3^b3)…(pm^bm)
其中最小公倍数=max(ai,bi);  最大公约数=min(ai,bi);

//素因子分解求最小公倍数,这个方法在有些数论问题分析中非常重要，主要掌握欧几里得算法就行了。
#include
using namespace std;
typedef long long  ll;
int main()
{
    ll n,m;
    while(cin>>n>>m)
    {
        int tn=n,tm=m;
        int count1,count2;
        ll lcm=1;
        ll mult1=1,mult2=1;
        for(int i=2; i<=max(n,m); i++)
        {
            if(tn%i==0||tm%i==0)
            {
                count1=count2;
                mult1=mult2=1;
                while(tn%i==0)
                {
                    count1++;
                    tn/=i;
                    mult1*=i;
                }
                while(tm%i==0)
                {
                    count2++;
                    tm/=i;
                    mult2*=i;
                }
                lcm=lcm*max(mult1,mult2);
            }
        }
        printf("%lld\n",lcm);
    }
    return 0;
}

• lcm函数求最小公倍数

可以防止a*b溢出

• gcd的一些性质
  gcd(a , b) = gcd(b , a-b)
  gcd(ma , mb) = m*gcd(a , b), m为一个自然数
  gcd(a+mb , b) = gcd(a , b)
  m=gcd(a , b) 则gcd(a/m,b/m)=gcd(a,b)/m
  gcd(a, lcm(b, c)) = lcm(gcd(a, b), gcd(a, c))
  lcm(a, gcd(b, c)) = gcd(lcm(a, b), lcm(a, c))

• 当然，在有些题目中我们要求求出很多个数的最大公约数和最小公倍数。
  对于这种问题，基本思想就是两两合并。例如求n个数的最大公约数，就可以这样：
  

• 下面开始AC
  1.多数求最大公约数
  给定n(n<=10)个正整数，你的任务就是求它们的最大公约数，所有数据的范围均在long long内。
  Input
  输入数据有多组，每组2行，第一行为n，表示要输入数字的个数，接下来第二行有n个正整数。
  Output
  输出一个数，即这n个数的最大公约数。
  Sample Input
  5
  2 4 6 8 10
  2
  13 26
  Sample Output
  2
  13

#include 
using namespace std;

int main()
{
    long long n,i,a[11];
    while(cin>>n)
    {
        for(i=1; i<=n; i++)
            cin>>a[i];
        for(i=1; i<=n-1; i++)
            a[i+1]=__gcd(a[i],a[i+1]);//核心
        printf("%lld\n",a[n]);
    }
    return 0;
}

2.多数求最小公倍数
给定n(n<=10)个正整数，你的任务就是求它们的最小公倍数，所有数据的范围均在long long内。
Input
输入数据有多组，每组2行，第一行为n，表示要输入数字的个数，接下来第二行有n个正整数。
Output
输出一个数，即这n个数的最小公倍数。
Sample Input
5
2 4 6 8 10
2
13 26
Sample Output
120
26

#include 
using namespace std;
long long lcm(long long a,long long b)
{
    return a/__gcd(a,b)*b;//写出lcm函数
}
int main()
{
    long long n,i,a[11];
    while(cin>>n)
    {
        for(i=1; i<=n; i++)
            cin>>a[i];
        for(i=1; i<=n-1; i++)
            a[i+1]=lcm(a[i],a[i+1]);//核心
        printf("%lld\n",a[n]);
    }
    return 0;
}

3.求区间中的数
最近沉迷于数论，她最近在研究最小公倍数和最大公约数，她的老师Z给她留了一个作业：在[x,y]区间中，求两个整数最大公约数是x且最小公倍数是y的个数。
Input
第一行输入一个T(T<=300)，表示有T组数据，接下来输入两个数 x, y(1<=x<=y<=1e6)(含义如题)
Output
输出一行表示答案
Sample Input
1
2 12
Sample Output
4
Hint
(2,12) (4,6) (6,4) (12,2)

#include 
using namespace std;
long long lcm(long long a,long long b)
{
    return a/__gcd(a,b)*b;
}
int main()
{
    long long n,i,a[11],m,x,y,j;
    while(cin>>n)
    {
        m=0;
        cin>>x>>y;
        for(i=x; i<=y; i++)//这个代码简单易懂，但是两个循环会超时
        {
            for(j=x; j<=y; j++)
            {
                if(__gcd(j,i)==x&&lcm(j,i)==y)
                    m++;
            }
        }
        printf("%d\n",m);
    }
    return 0;
}

所以再来一个

#include
using namespace std;
int t;
long long x, y;
int main()
{
    cin>>t;
    while(t--)
    {
        int cnt=0;
        cin>>x>>y;
        long long p = x*y;
        for(long long i=x; i<=y; i++)
            if(p%i==0)//把上面的循环换成if判断
                if(p/i>=x && p/i<=y && __gcd(i, p/i)==x)//核心
                    cnt++;
        cout<<cnt<<endl;
    }
    return 0;
}

• 下节提示

acm新手小白必看系列之（7）——快速幂精讲及例题