浪潮之巅-深度学习在推荐系统中的应用（深度学习推荐系统学习笔记）

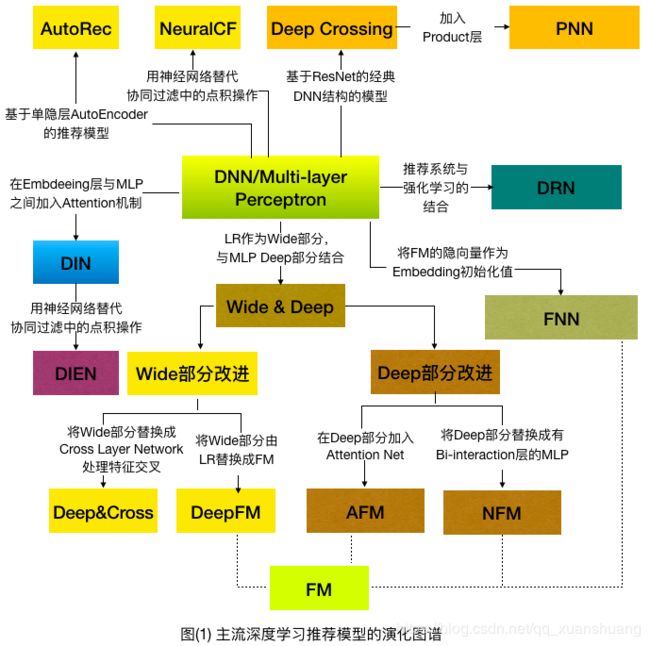
1 深度学习推荐模型的演化关系图

2 AutoRec-单隐层神经网络推荐模型

将自编码器的思想同协同过滤结合，是一种单隐层神经网络推荐模型。

2.1 AutoRec模型的基本原理

利用协同过滤中的共现矩阵，完成物品向量或者用户向量的自编码，再利用自编码的结果得到用户对物品的预估评分，进而进行推荐排序。

自编码器：

设是数据向量，将作为输入，通过自编码器是得到的输出向量尽可能接近其本身。设自编码器的重建函数为，则自编码器的目标函数：

        

其中，S是所有数据向量的集合

AutoRec解决的问题是构建一个重建函数，是所有该重建函数生成的评分向量与原评分向量的平方残差和最小，如(1)式所示，此后还要经过评分预估和排序的过程才能得到最终的推荐列表。

2.2 AutoRec模型的结构

          

输入层：原始评分向量，中间层：k()维单隐层，输出层：多分类层。重建函数如式(2)，其中f和g是激活函数：

        

目标函数，加入L2正则化

         

AutoRec模型是一个非常标准的三层神经网络，训练利用梯度反向传播即可。

2.3 基于AutoRec模型的推荐过程

当输入物品i的评分向量时，模型的输出向量就是所有用户对物品i的评分预测，其中第u维就是用户u对物品i的预测

       

通过遍历输入物品向量就可以得到用户u对所有物品的评分预测，进而依据评分预测进行排序得到推荐列表。

同协同过滤，AutoRec也分为基于物品的AutoRec（I-AutoRec）和基于用户的AutoRec（U-AutoRec），U-AutoRec是将用户的评分向量作为输入数据，在生成推荐列表的时候，U-AutoRec相比I-AutoRec优点是只需要输入一次目标用户的用户向量，而I-AutoRec需要遍历整个物品评分向量；缺点是用户向量的稀疏性可能会影响模型效果。

2.4 AutoRec模型的特点和局限性

优点：从神经网络角度出发，使用一个单隐层的AutoEncoder泛化用户或物品评分，具有一定的泛化能力和表达能力

缺点：比较简单，表达能力相对欠缺

在模型结构上，该模型和后来的词向量模型（Word2vec）完全一致，但优化目标和训练方法有所不同。

3 Deep Crossing模型-经典的深度学习架构

Deep Crossing模型完整的解决了从特征工程、稀疏向量稠密化、多层神经网络进行优化目标拟合等一系列深度学习在推荐系统中的应用问题。

3.1 Deep Crossing模型的网络结构

为完成端到端的训练Deep Crossing模型要在其内部解决如下问题：

1. 离散类特征编码后过于稀疏，不利于直接输入神经网络进行训练，如何解决稀疏特征向量稠密化的问题
2. 如何解决特征自动交叉的问题
3. 如何在输出层中打成问题设定的优化目标

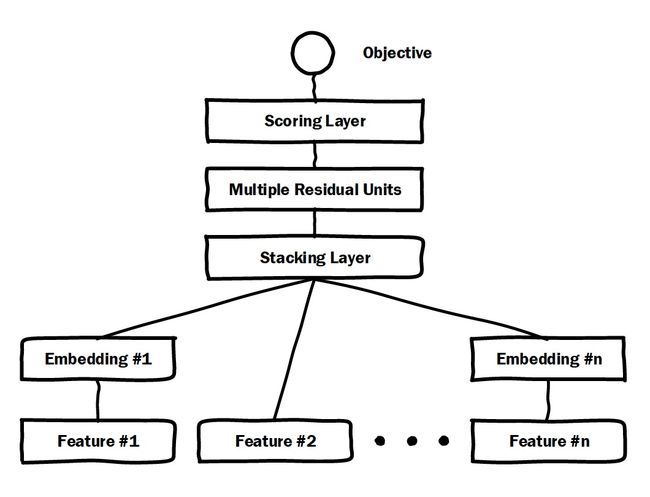
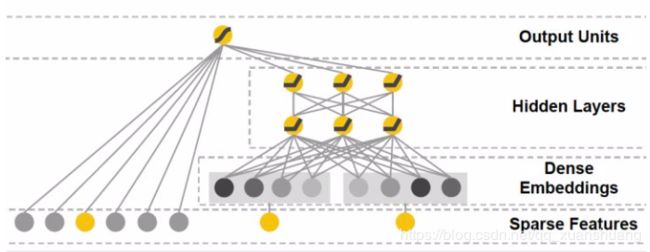
通过加入embedding层将稀疏特征转化为低维稠密特征，用stacking layer，或者叫做concat layer将分段的特征向量连接起来，再通过多层神经网络完成特征的组合、转换，最终用scoring layer完成CTR的计算。跟经典DNN有所不同的是，Deep crossing采用的multilayer perceptron是由残差网络组成的。

       

Embedding层：将稀疏的类别性特征转换成稠密的Embedding向量，以经典的全连接层结构为主。通常，Embedding向量的维度应该远小于原始稀疏特征向量。这里Feature #2世纪代表了数值型特征，可以看到，数值型特征不需要经过Embedding层，直接进入了Stacking层。

Stacking层：Stacking层（堆叠层）的作用比较简单，是把不同的Embedding特征和数值型特征拼接在一起，也被称为连接（concatenate）层。

Multiple Residual Units层：主要结构时多层感知机，相比标准的多层感知机为基本单元的神经网络，Deep Crossing模型采用了多层残差网络（Multi-Layer Residual Network）作为MLP的具体实现。通过多层残差网络对特征向量各个维度进行充分的 交叉组合。

Scoring层：Scoring层作为输出层，就是为了拟合优化目标，对CTR预估这类二分类问题，Scoring层往往使用的是逻辑回归模型，对于图像等多分类问题，Scoring层往往采用softmax模型。

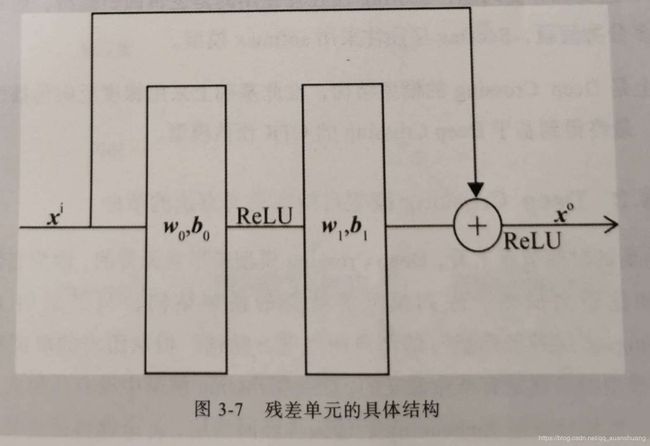
残差神经网络：

残差神经网络是由残差单元组成的神经网络。与传统感知机不同，残差单元的特点主要有：

1. 输入经过一层以ReLu为激活函数的全连接层后再经过一层全连接层，生成输出向量
2. 输入可以通过一个短路通路直接与输出向量进行元素加（element-wise plus）操作，生成最终的输出向量。

这样的结构下，残差单元中的两层ReLu网络其实拟合的是输出和输入之间的残差（）。

主要解决两个问题：

1. 神经网络是不是越深越好？深度加深后，容易产生过拟合，在残差网络中，由于有输入向量段路的存在，很多时候可以越过两层ReLu网络，减少过拟合现象发生。
2. 当神经网络过深时，往往存在严重的梯度消失现象，梯度消失现象是指在梯度反向传播的过程中，越靠近输入端，梯度的幅度越小，参数收敛的速度越慢。为了解决这个问题，残差单元使用ReLu激活函数取代了原来的sigmoid函数，此外，输入向量短路相当于直接把梯度毫无变化的传递到下一层，也使残差网络的收敛速度更快。

3.2 Deep Crossing模型对特征交叉方法的革命

采用了“Embedding+多层神经网络”。相比之前的FM、FFM模型只具备二阶特征交叉的能力，Deep Crossing模型可以通过调整神经网络的深度进行特征之间的“深度交叉”。

4 NeuralCF模型-CF与深度学习的结合

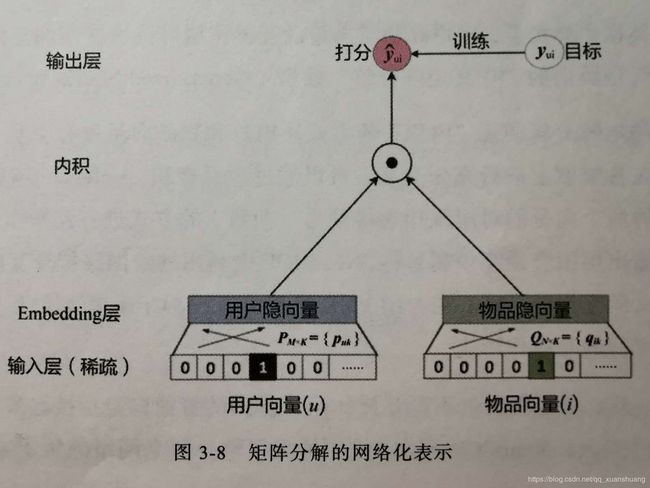
4.1 从深度学习的视角重新审视矩阵分解模型

若将矩阵分解层的用户隐向量和物品隐向量看作是一种Embedding方法，最终的“Scoring层”就是将用户隐向量和物品隐向量进行内积操作后得到的“相似度”，这里的相似度就是对评分的预测。在实际应用中，往往发现模型容易欠拟合，主要原因是MF的模型结构相对简单，尤其“Scoring层”，无法对优化目标进行有效的拟合。

        

4.2 NeuralCF模型的结构

      

NeuralCF用“多层神经网络+输出层”的结构替代了MF中简单的内积操作，优点如下：1、让用户向量和物品向量左更充分的交叉；2、引入更多的非线性特征。

事实上，用户向量和物品向量的互操作层可以被任意的互操作形式所替代，即所谓的广义矩阵分解模型（Generalized Matrix Factorization）。为了让向量在各维度上进行更充分的交叉，可以通过“元素积”（element-wise product，长度相同的两个向量按元素乘得到新的同维度的向量）进行交互，再通过逻辑回归等输出层拟合最终预测目标，当然还有别的交互方式。GMF，它应用了一个线性内核来模拟潜在的特征交互；MLP，使用非线性内核从数据中学习交互函数

     

其中GMF层和MLP层是两个子网络，即GMF和MLP可以学习独立的嵌入，也即MLP的用户、物品向量的维度可以和GMF的用户、物品的维度可以不相同，其中GMF的输入MF模型得到的是用户隐向量和物品隐向量。

softmax

给定一个n维向量，softmax函数将其映射维一个概率分布，标准的softmax函数由下面的公式定义：

        

softmax解决了从一个原始的n维向量，向一个n维的概率分布映射的问题。在多分类中，设n是类别数，模型期望预测的就是某个样本在n个分类上的概率。若用深度学习模型进行建模，输出层是由n个神经单元组成的，再辅以softmax激活函数，在最后的输出中得到最终的多分类概率分布。

        

在分类问题中，softmax函数往往和交叉熵损失函数配套使用（因为softmax函数把分类输出标准化成了多个分类的概率分布，而交叉熵正好刻画了预测分类和真实结果之间的相似度）：

         

softmax函数的导数：

          

基于链式法则，交叉熵函数到softmax函数第j维输入的导数形式为：

         

多分类，真实值只有一个维度是1，其余维度都是0，假设第k维是1，即，则交叉熵损失函数可以简化为：
         

则

        

4.3 NeuralCF模型的优势和局限性

优点：对于用户向量和物品向量这俩Embedding层可以自由的选择不同互操作层的拼接。

缺点：基于协同过滤的思想，没有引入更多其他类型的特征

5 PNN模型-加强特征交叉能力

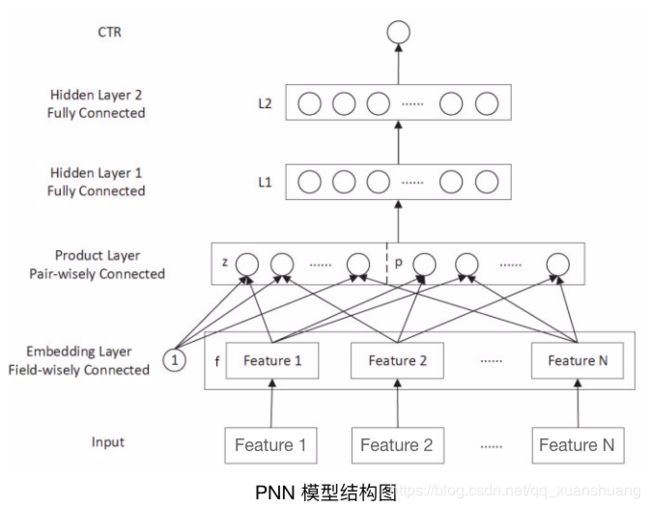
5.1 PNN模型的网络架构

        

与Deep Crossing模型相比，PNN模型在输入、Embedding层、多层神经网络，以及最终的输出层部分并没有结构上的不同。唯一的区别在于PNN模型用乘积层（Product Layer）代替了Deep Crossing模型中的Stacking层，即不同特征的Embedding向量不再是简单的拼接，而是利用Product操作进行两两交互。

5.2 Product层的多种特征交叉方式（外积部分还是没懂，待学习）

PNN 模型对于深度学习结构的创新主要在于乘积层的引入。具体地说，PNN 模型的乘积层由线性内积操作部分(图中乘积层的 z 部分，对各特征向量进行线性拼接)和乘积外积(outer product) 操作部分(图中乘积层的 p 部分)组成。其中，乘积特征交叉部分又分为无论是内积操作和还是外积 操作，使用内积操作的PNN模型被称为IPNN（Inner Product-based Neural Network），使用外积操作的PNN被称为OPNN（Outer Product-based Neural Network）。

首先看z部分，这一块是线性部分，其实就相当与把Embedding层的特征拿过来，组成一个向量即可。
z=concat([emb1,emb2..,embn],axis=1)，形如(bs,fs*emb)的张量

IPNN

IPNN就是实现两个向量的点乘，得到的是一个数。思路就是将所有特征的embedding表示两两相乘，可以得到一个长度为的向量。内积操作就是经典的向量内积运算设输入特征向量分别为，特征的内积操作，若设特征数为n，则这样两两交叉得到个值，即填入p中的元素形如(bs,pairs)，正好可以和z部分进行concat：

        

之前还不太明白两两交互的实现，后来在网上找到了实现，mark一下，https://github.com/Hirosora/LightCTR/blob/master/models/PNN.py，

https://blog.csdn.net/qq_18293213/article/details/90262378。假设batch_size=3，特征数fs=5，Embedding维度vec=8，现在解释一下下面这段程序，其中inputs是一个列表，列表的长度5（特征的个数），其中每一个元素都是一个形如(bs,vec)的特征的张量，然后rows和cols相同位置的值是列表中要做两两交叉的特征的下标，下面给出rows和cols的值，可以看出此处是对。

len(rows) = 10, rows = [0, 0, 0, 0, 1, 1, 1, 2, 2, 3]
len(cols) = 10, cols = [1, 2, 3, 4, 2, 3, 4, 3, 4, 4]

p和q是分别按照rows和cols中的下标取出的对应的inputs中的特征的张量在axis=1上的堆叠，即pairs个形如(bs,vec)的张量在axis=1上的堆叠，得到形如(bs,pairs,vec) 的张量，p和q同位置的元素按元素乘，在对vec这一维度reduce_sum，其实就是两两内积的一种实现方式。

p = Tensor("model/inner_product/stack:0", shape=(3, 10, 8), dtype=float32)
q = Tensor("model/inner_product/stack_1:0", shape=(3, 10, 8), dtype=float32)
inner_product = Tensor("inner_product/Sum:0", shape=(None, 10), dtype=float32)

    def call(self, inputs, **kwargs):

        rows = list()
        cols = list()
        for i in range(len(inputs)):
            for j in range(i + 1, len(inputs)):
                rows.append(i)
                cols.append(j)

        # [batch_size, pairs_num, embedding_size]
        print("len(rows) = {}, rows = {}".format(len(rows), rows))
        print("len(cols) = {}, cols = {}".format(len(cols), cols))
        print("len(inputs), inputs[0].shape = {}".format(len(inputs), inputs[0].shape))
        p = tf.stack([inputs[i] for i in rows], axis=1)
        q = tf.stack([inputs[j] for j in cols], axis=1)
        print("p = {}".format(p))
        print("q = {}".format(q))

        if self.require_logit:
            inner_product = tf.reduce_sum(p * q, axis=-1, keepdims=False)
        else:
            inner_product = tf.keras.layers.Flatten()(p * q)
        print("inner_product = {}".format(inner_product))
        return inner_product

 

OPNN

两个向量内积得到的是一个数，故内积操作可以得到形如(bs,pairs)的张量，但是两个向量外积是同维度的向量，故外积操作得到形如(bs,pairs,vec)的张量，不容易进行concat，计算量也比较大，OPNN做了简化。

5.3 PNN模型的优点和缺点

优点：特征Embedding向量之间的交叉方式是多样的

缺点：实践中，会对外积操作做一系列简化；对所有特征无差别的交叉忽略了原始特征向量中包含的有价值的信息。

6 Wide & Deep 模型 - 记忆能力和泛化能力的综合

Wide部分主要作用是让模型具备较强的“记忆能力”；Deep部分的主要作用是让模型具有“泛化能力”。

6.1 模型的记忆能力与泛化能力

“记忆能力”：模型直接学习并利用历史数据中的物品或者强特征的“共现频率”的能力。一般来说，协同过滤、逻辑回归等简单模型具有较强的“记忆能力”。这类模型结构简单，没有过多的特征交叉，原始数据往往可以直接影响推荐结果，产生类似于”若点击过A则推荐B“这类规则式的推荐，相当于模型直接记住了历史数据的分布特点，并利用这些记忆进行推荐。多层神经网络特征会被多层处理，不断与其他特征交叉，使得模型对原始强特征的记忆反而不如简单模型。

“泛化能力”：模型传递特征的相关性，以及发觉稀疏甚至从未出现过的稀有特征与最终标签相关性的能力。矩阵分解比协同过滤的泛化能力强，因为MF引入了隐向量，使得数据稀少的用户或者物品也能生成隐向量，从而获得由数据支撑的推荐得分，这就是典型的将全局数据传递到稀有物品上，从而提高泛化能力。再如，深度神经网络通过特征次组合，可以发掘数据中潜在的模式，即使非常稀疏的特征向量输入，也能得到较稳定平滑的推荐概率。

6.2 Wide & Deep 模型结构

          

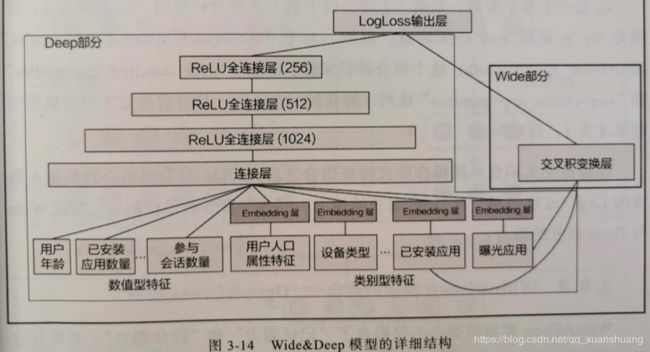
单层的Wide部分擅长处理大量稀疏的id类特征；Deep部分利用神经网络强大的表达能力，进行深层的特征交叉，挖掘藏在特征背后的数据模式。

          

图（3-14）是Google Play的推荐团队用的详细结构，Wide部分的输入仅仅是以安装应用和曝光应用两类特征，其中已安装应用代表用户历史行为，而曝光应用代表当前的待推荐应用，选择这两类特征的原因是充分发挥Wide部分记忆能力强的优势，简单模型善于记忆用户行为特征中的信息，并依据此类信息直接影响推荐结果。

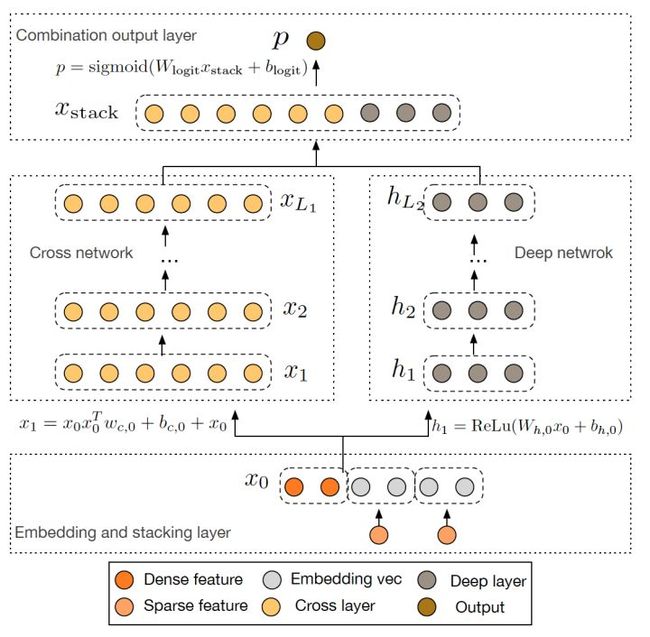
6.3 Wide&Deep模型的进化-Deep&Cross模型

          

Deep&Cross模型主要思路是使用Cross网络代替了原来的Wide部分。Cross部分是为了增加特征之间的交互力度，使用多层交叉层对输入向量进行特征交叉，设第l层交叉层的输出向量是，则第l+1层的输出向量：

            

可以看到，交叉层操作的二阶部分非常类似PNN模型中的外积操作，在此基础上增加了外积操作的权重向量，以及原输入向量和偏置向量，其中的结果是一个矩阵，通过与的矩阵乘法得到一个向量。

          

举个

         

        

可以看出特征交叉的感觉，但是交叉层在增加参数方面还是比较克制的，每一层仅增加了一个n维（输入向量的维度）的权重向量，并且每一层均保留了原始 输入向量，所以输出与输入之间的变化不会太明显。

6.4 Wide&Deep模型的影响力

1. 抓住了业务问题的本质，能融合传统模型的记忆能力和深度神经网络的泛化能力
2. 模型结构并不复杂。

7 FM与深度学习模型的结合

 

 

 

 

 

 

 

 

 

 

 

未完待续

 

 

 

 

 

 

 

 

 

 

 

 

 

参考 ：深度学习推荐系统，王喆