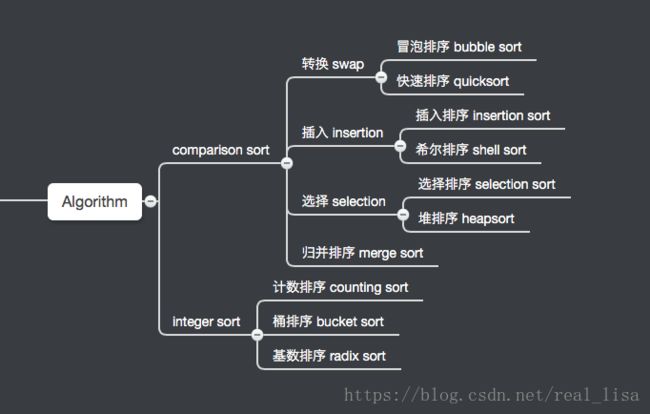
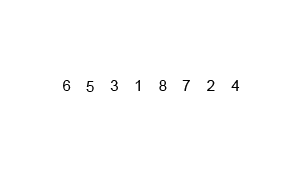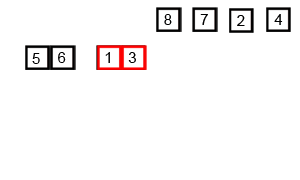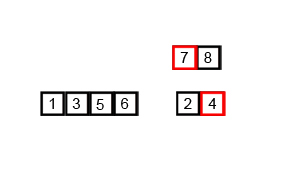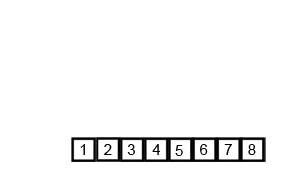常见十大(内部)排序算法 - Sorting Algorithms C++

基本概念

---

内部和外部排序

内部排序在这里指的是只用到了电脑内存而不使用外存的排序方式。相对的，外部排序就是同时动用了电脑内存和外存的排序方式。本文在这里只讨论内部排序。

分类

比较和非比较排序

比较在这里指的是需要比较两个元素的大小(前后)才能进行的排序。难道有排序算法不需要比较吗？的确有，但是不多。常见的有三种：计数排序，桶排序，基数排序。它们用统计的方法规避了比较，详细的可查看之后讲到的这些算法。

转换

每次只调换两个元素之间的位置。

插入

遍历到的元素放入之前维护的已完成排序的序列中。

选择

选择剩余元素中最大或最小的元素。

 

知道了以上概念后，就能更好的看懂分类了（建议先略看，看完所有排序算法后再回看）

 

稳定度 (Stability)

定义：如果排序算法并不改变两个相同值的元素的相对位置，则此算法稳定度高。

这张图十分形象地解释了以上定义：

这个概念为什么重要？如果是稳定算法的话，我们可以先排序名，在排序姓。

(from:https://stackoverflow.com/questions/1517793/what-is-stability-in-sorting-algorithms-and-why-is-it-important）

 

冒泡排序 (Bubble Sort) 

---

1 算法

从第一个元素开始遍历，比较当前元素跟下一个元素的大小，如果不符合排序，交换位置。结束最后一个元素后，再从头开始不断遍历，直到完成排序。

剖析：每遍历完一次，最小数前进一位，但是最大数到达最终位；末尾已经是最终排序。

2 代码

基本

void bubble(vector& arr){
	for(int i=0;iarr[j+1]) swap(arr[j],arr[j+1]);
			//arr[j]>arr[j+1] stable
			//arr[j]>=arr[j+1] unstable
		}
	}
}

优化1: 每遍历完一遍，看是否已经提前完成排序(用 hasSorted)。如是，提早结束。

void bubble1(vector& arr){
	bool hasSorted = false;
	for(int i=0;iarr[j+1]){
				hasSorted = false;
				swap(arr[j],arr[j+1]);
			}
		}
	}
}

优化2:  根据“剖析：每遍历完一次，最小数前进一位，但是最大数到达最终位；末尾已经是最终排序。”，每遍历完一次，里面的loop就可以少遍历一个元素。但其实由此我们可以推论，最后一个swap的j和j+1, j之后的元素(不包括j)都已经完成排序了。

void bubble2(vector& arr){
	int n = arr.size()-1;
	for(int i=0;iarr[j+1]){
				upto = j;		//upto=j不定大小的最后一位, j+1 已经完成排序（最后一个if）
				swap(arr[j],arr[j+1]);
			}
		}
		n=upto;
		if(n==0) break;
	}
}

优化3: 可以进行双向的循环，正向循环把最大元素移动到末尾，逆向循环把最小元素移动到最前，这种优化过的冒泡排序，被称为鸡尾酒排序(Cocktail Sort)

void bubble4(vector& arr){
	int beg = 0;
	int end = arr.size()-1;
	while(begarr[i+1]){
				nend=i;
				swap(arr[i],arr[i+1]);
			}
		}
		if(nend==end) break;
		end = nend;

		//逆向循环
		for(int i=end; i>beg;i--){
			if(arr[i]

3 分析

3.1 稳定度

决定于比较的时候用的是大于等于(小于等于)还是大于(小于)

arr[i]>arr[i+1] --> 稳定

arr[i]>=arr[i+1] --> 不稳定

3.2 时间

逆向排序时是最差的情况，O(n^2)

3.3 空间

需要O(1)来完成swap等

 

快速排序 (Quicksort)

---

1 算法

利用了 divide & conquer 的思想。

在序列中任意选择一个数，然后把序列分成比这个数大的和比这个数小的两个子序列。不断重复以上步骤完成排序。

2 代码

int partition1(vector& arr, int beg, int end){
	int pivot = arr[beg];
	int l=beg+1, r=end;
	while(l<=r){
		if(arr[l]pivot) r--;
		else if(arr[l]>=pivot && arr[r]<=pivot){
			swap(arr[l++], arr[r--]);
		}
	}
	swap(arr[r], arr[beg]);
	return r;
}

int partition2(vector& arr, int beg, int end){
	int pivot = arr[beg];
	int index = beg+1;
	for(int i=index;i<=end;i++){
		if(arr[i]& arr, int beg, int end){
	if(beg

优化1 切换到插入排序

因为快速排序在小数组中也会递归调用自己，对于小数组，插入排序比快速排序的性能更好，因此在小数组中可以切换到插入排序。

优化2 三数取中

最好的情况下是每次都能取数组的中位数作为切分元素，但是计算中位数的代价很高。人们发现取 3 个元素并将大小居中的元素作为切分元素的效果最好。

优化3 三向切分

对于有大量重复元素的数组，可以将数组切分为三部分，分别对应小于、等于和大于切分元素。

等之后review的时候再贴code吧～ 写这个太烧脑了～

3 分析

3.1 稳定度

3.2 时间

最好的情况是pivot都是中点 -- O(n log n) (平均情况也是如此，所以有些快排算法会在一开始随意打乱数列)

最差的情况是本来就是有序数列 -- O(n^2)

3.3 空间

尽管没有用另外的数据结构，但是不是O(1)哦～ 因为recursion需要在stack frames里面重新建array。我上面的code需要O(n) extra space, 最优的话，可以达到O(log n)

4 变形

LeetCode - Top K Frequent Elements

 

插入排序 (Insertion Sort)

---

1 算法

维护一段有序数列，同时遍历待排序的数列，在有序数列里找到合适的位置，插入元素。

2 代码

void insertion(vector& arr){
	for(int i=1;i=0;j--){
			if(arr[temp]

优化1 找到当前元素该插入的位置后，再插入

void insertion1(vector& arr){
	for(int i=1;i=0 && temp

3 分析

3.1 稳定度

arr[temp]

3.2 时间

最优情况是正向排序 -- O(n)

最差是逆向排序，每次插入都需要比较已完成数列元素的个数 -- O(n^2)

3.3 空间

O(1) - 如上code -> temp

 

希尔排序 (Shell Sort)

---

1 算法

简单插序的改进版，选择先插入距离远的元素。

选择一个间距，将序列分成很多子序列并进行插入排序。降低间距并重复插入排序，直到间距降为1完成排序。

2 代码

//只需要把之前insert function的gap=1改成变量gap就行
void shellInsert(vector& arr, int beg, int gap){
	for(int i=beg+gap;i=0 && temp& arr){
	int gap = arr.size()/2;
	while(gap>0){
		int beg=gap-1;
		while(beg>=0){
			shellInsert(arr, beg, gap);
			beg--;
		}
		gap = gap/2;
	}
}

3 分析

3.1 稳定度

对于相同的两个数，可能由于分在不同的组中而导致它们的顺序发生变化。

3.2 时间

希尔排序的时间复杂度与增量(即，步长gap)的选取有关。例如，当增量为1时，希尔排序退化成了直接插入排序，此时的时间复杂度为O(N²)，而Hibbard增量的希尔排序的时间复杂度为O(N3/2)。

3.3 空间

O(1) - 如上code -> temp

3.4 对比其他算法

当gap最大时，相当于bubble sort; 当gap=1时，就相当于insertion sort。

 

选择排序 (Selection Sort)

---

1 算法

维护一段有序数列，同时遍历待排序的数列，通常找最小的元素插入到有序数列中。重复直到待排序数列没有剩余元素。

2 代码

void select(vector& arr){
	int s = arr.size();
	for(int i=0;i

3 分析

3.1 稳定度

arr[j]

3.2 时间

无论好坏都需要O(n^2), 因为每次选出最小值都需要遍历所有剩余元素。

3.3 空间

O(1)

 

堆排序 (Heapsort)

---

1 算法

了解推(Heap)

2 代码

3 分析

3.1 稳定度

3.2 时间

3.3 空间

 

归并排序 (Mergesort)

---

1 算法

利用了 divde & conquer 的思维方式，有时候也称为合并排序。

将序列不断分解为子序列直到只剩于0或1位。再将子序列不断按大小合并，最终恢复为原来序列的长度。

2 代码

vector merge(vector a, vector b){
	vector res;
	int ba = 0;
	int bb = 0;

	while(ba mergeSort(vector arr){
	int s = arr.size();
	if(s<2) return arr;
	int mid = s/2;
	vector front(arr.begin(), arr.begin()+mid);
	vector back(arr.begin()+mid, arr.end());
	return merge(mergeSort(front), mergeSort(back));

}

3 分析

3.1 稳定度

a[ba]<=b[bb] -- 当元素相等时并不改变元素的前后位置, 所以归并排序是稳定的。

3.2 时间

每次都将子序列分为母序列的一半，所以O(n log n)

3.3 空间

需要另外的空间来存子序列 -- O(n)

 

计数排序 (Counting Sort)

---

1 算法

顾名思义统计待排序数列中每个数字出现的次数。填入数据结构的过程其实就是排序的过程。最后再按照统计结果覆盖原序列就行了。

2 代码

void count(vector& arr, int range){
	vector temp(range+1, 0);
	for(int i=0;i

3 分析

不是基于比较的排序，但是前提条件是知道排序元素的范围。

3.1 稳定度

stable - https://stackoverflow.com/questions/2572195/how-is-counting-sort-a-stable-sort

3.2 时间

O(n+k), k为range

3.3 空间

O(n+k), 用来存计数结果

 

桶排序 (Bucket Sort)

---

1 算法

基于计数排序，增加了函数映射(hashmap)，把元素归于不同的桶中便于排序。

比如说，需要排序1-100的数字。如果是计数排序，就需要一个100的vector来存；桶排序可以用一个10的vector来存，每个元素进入(元素/10)index的vector。

2 代码

因为不同数据对函数映射的要求不同，这里就不贴代码了。

3 分析

3.1 稳定度

3.2 时间

最好 - O(n+k)

最差 - O(n^2)

3.3 空间

O(n*k)

 

基数排序 (Radix Sort)

---

1 算法

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。

2 代码

贴个别人家的

// LSD Radix Sort
var counter = [];
function radixSort(arr, maxDigit) {
    var mod = 10;
    var dev = 1;
    for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
        for(var j = 0; j < arr.length; j++) {
            var bucket = parseInt((arr[j] % mod) / dev);
            if(counter[bucket]==null) {
                counter[bucket] = [];
            }
            counter[bucket].push(arr[j]);
        }
        var pos = 0;
        for(var j = 0; j < counter.length; j++) {
            var value = null;
            if(counter[j]!=null) {
                while ((value = counter[j].shift()) != null) {
                      arr[pos++] = value;
                }
          }
        }
    }
    return arr;
}

3 分析

3.1 稳定度

3.2 时间

基数排序基于分别排序，分别收集，所以是稳定的。但基数排序的性能比桶排序要略差，每一次关键字的桶分配都需要O(n)的时间复杂度，而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字，则基数排序的时间复杂度将是O(d*2n) ，当然d要远远小于n，因此基本上还是线性级别的。

3.3 空间

基数排序的空间复杂度为O(n+k)，其中k为桶的数量。一般来说n>>k，因此额外空间需要大概n个左右。

 

Reference:

https://www.cnblogs.com/onepixel/articles/7674659.html

https://blog.csdn.net/hguisu/article/details/7776068

https://github.com/francistao/LearningNotes/blob/master/Part3/Algorithm/Sort/面试中的%2010%20大排序算法总结.md