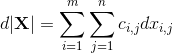shiyueyue0822
shiyueyue0822

矩阵求导术的故事

\mathbf{a_{m\times1}}, \mathbf{X_{m\times n}},\mathbf{b}_{n\times 1}转自知乎，感谢大神长躯鬼侠

1. 标量对矩阵的求导

2.矩阵对矩阵的求导

作为一个数学渣渣，那些能把复杂难懂的数学公式和过程讲的简单易懂的人是我的本命。在机器学习中存在许多求导过程，在论文中推导也是很重要的一环。我花了3天时间阅读并学习了以上两个奇术。为了能完整消化并掌握，我内容写到这里，权当笔记。

一.  标量对矩阵求导

矩阵导数可以和微分联系起来。微分是矩阵导数和微分矩阵的内积。

df = \sum_{i=1}^{m}\sum_{j=1}^{n}\frac{\partial f}{\partial \mathbf{X}_{i,j}}d\mathbf{X}_{i,j}=tr(\frac{\partial f^{T}}{\partial\mathbf{ X}}d\mathbf{X})

tr在这里为矩阵的迹，它的值是对角线上的元素之和，即两个矩阵对应元素相乘之和。

因此在求解标量对矩阵的导数时，先把df求出来，即先求矩阵微分，转换为迹 因为标量的迹等于标量，通过迹把其他元素都挪到d\mathbf{\mathbf{X}}的右边，即可求出标量对矩阵的导数转置\frac{\partial f^{T}}{\partial \mathbf{X}}。

在求解中会遇到一些复杂的复合函数，因此规定了一些运算规则。包括矩阵微分的计算规则和迹的计算规则。

1. 矩阵微分的计算规则

1) 加减法  d(\mathbf{X}\pm \mathbf{Y}) = d\mathbf{X} \pm d\mathbf{Y}  

   乘法      d(\mathbf{XY}) = \mathbf{X}d\mathbf{Y} + (d\mathbf{X})\mathbf{Y}

   转置      d(\mathbf{\mathbf{X}}^{T}) = (d\mathbf{X})^{T}

2) 逆        d\mathbf{X}^{-1} = -\mathbf{X}^{-1}d\mathbf{XX}^{-1}     对 \mathbf{XX}^{-1}=I两侧求导可以推出

3）行列式  d\left | \mathbf{X} \right | = tr(\mathbf{X}^{\#}d\mathbf{X})     \mathbf{X}^{\#}是伴随矩阵，是代数余子式构成的矩阵的转置。\mathbf{X}^{\#}\mathbf{X}=|\mathbf{X}|E

                 推导过程：d|\mathbf{X}| = \sum_{i=1}^{m}\sum_{j=1}^{n}c_{i,j}dx_{i,j}

4) 逐元素乘法  d(\mathbf{A}\odot \mathbf{B} )=\mathbf{A}\odot d\mathbf{B} + d\mathbf{A}\odot \mathbf{B}    \odot运算是两个相同大小的矩阵对应元素相乘。主要用到的原因是导数与元素出来是对应元素相乘。

5）逐元素函数  d\sigma (\mathbf{X}) = \sigma(\mathbf{X}){}' \odot d\mathbf{X}

2. 迹的运算规则

1）加减     tr(\mathbf{A}\pm\mathbf{ B}) =tr(\mathbf{A}) \pm tr(\mathbf{B})

2） 乘        tr(\boldsymbol{AB}) = tr(\mathbf{BA})

3）  转置     tr(\mathbf{A}^{T}) = tr(\mathbf{A})

 4） 标量     a = tr(a)    此处用处很多，大部分第一二步就可以用了

  5）逐元素乘法   tr(\mathbf{A}^{T}(\mathbf{B}\odot \mathbf{C})) = tr((\mathbf{A}\odot\mathbf{ B})^{T} \mathbf{C})       没有推导，但等式两边都等于 \sum_{i=1}^{i=m}\sum_{j=1}^{j=n}A_{i,j}B_{i,j}C_{i,j}    ，这一运算用于2(5)通常在将逐元素函数后为了把d\mathbf{X}分离出来。

例1 f =\mathbf{ a^{T}Xb}  求  \frac{\partial f^{T}}{\partial \mathbf{X}}. 其中  \mathbf{a_{m\times1}}, \mathbf{X_{m\times n}},\mathbf{b}_{n\times 1}.

解：先求微分

     df = d\mathbf{a}^{T}\mathbf{X}\mathbf{b} = \mathbf{a}^{T}d\mathbf{X}\mathbf{b}    

     使用迹运算，由于f是标量，那么df也是标量。那么根据标量的迹运算可得

      \\ df = tr(df)\\ =tr( \mathbf{a}^{T}d\mathbf{X}\mathbf{b})\\ = tr(\mathbf{b} \mathbf{a}^{T}d\mathbf{X})\\ =tr( (\mathbf{a}\mathbf{b}^{T})^{T}d\mathbf{X})\\ =tr(\frac{\partial f^{T}}{\partial \mathbf{X}}d\mathbf{X})
      在迹中把d\mathbf{X}挪到了最右，其中只在第一个等号和第三个等号分别使用了标量的迹运算和矩阵乘法的迹运算（交换相等）。

      则  \frac{\partial f}{\partial \mathbf{X}} = \mathbf{a}\mathbf{b}^T.

 

例2  f =\mathbf{ a^{T}exp(Xb)},  求  \frac{\partial f^{T}}{\partial \mathbf{X}}，其中\mathbf{a_{m\times1}}, \mathbf{X_{m\times n}},\mathbf{b}_{n\times 1}

解：先令\mathbf{h}=\mathbf{X}\mathbf{b}

       求微分

       \\ df = d(\mathbf{a}^{T}exp(\mathbf{h})) = \mathbf{a}^{T}(exp(\mathbf{h})\odot d\mathbf{h})

      根据标量迹法则

      \\ df = tr(df) = tr(\mathbf{a}^{T}(exp(\mathbf{h})\odot d\mathbf{h})) = tr((\mathbf{a}\odot exp(\mathbf{h}))^{T}d\mathbf{h})

       第一个等号用到了标量迹法则，第二个等号用到了矩阵微分的逐项函数求导法则，第三个等号用到了迹运算的逐项乘法法则。

        则，\frac{\partial f}{\partial \mathbf{h}} =\mathbf{a}\odot exp(\mathbf{h})

      继续，

    \\ df = tr(df) \\ = tr((\mathbf{a}\odot exp(\mathbf{h}))^{T}d\mathbf{h})\\ =tr(\frac{\partial{f^{T}}}{\partial \mathbf{h}}d\mathbf{h}) \\ = tr(\frac{\partial{f^{T}}}{\partial \mathbf{h}}(d\mathbf{X})\mathbf{b} )\\ = tr(\mathbf{b}\frac{\partial{f^{T}}}{\partial \mathbf{h}}(d\mathbf{X}) )\\ = tr((\frac{\partial{f}}{\partial \mathbf{h}}\mathbf{b}^{T})^{T}(d\mathbf{X}) )

   因此，\frac{\partial f}{\partial \mathbf{X}} =(\mathbf{a}\odot exp(\mathbf{h}))\mathbf{b}^{T}

例3  f = tr(\mathbf{Y}^T\mathbf{M}\mathbf{Y}),  \mathbf{Y}=\sigma (\mathbf{WX}), \mathbf{W}_{l\times m},\mathbf{X}_{m\times n},\mathbf{M}_{l\times l}, \mathbf{M}为对称矩阵  求\frac{\partial f^{T}}{\partial \mathbf{X}}

解：先求微分

       \\ df = tr(d(\mathbf{Y}^{T}\mathbf{M}\mathbf{Y})) \\ = tr((d\mathbf{Y})^{T}\mathbf{M}\mathbf{Y} ) + tr(\mathbf{Y}^{T}\mathbf{M}d\mathbf{Y}) \\ = tr(\mathbf{Y}^T\mathbf{M}^Td\mathbf{Y}) + tr(\mathbf{Y}^{T}\mathbf{M}d\mathbf{Y})\\ = tr(2\mathbf{Y}^T\mathbf{M}d\mathbf{Y}) \\ = tr((2\mathbf{M}^T\mathbf{Y})^{T}d\mathbf{Y})

     第2和第3个等号用了迹运算乘法和加减法法则,第2个等号用了迹运算转置法则。

     因此，

     \frac{\partial f}{\partial \mathbf{Y}} = 2\mathbf{M}^{T}\mathbf{Y}

     继续，TODO

     \\ df = tr(d(\mathbf{Y}^{T}\mathbf{M}\mathbf{Y})) \\ = tr((2\mathbf{M}^T\mathbf{Y})^{T}d\mathbf{Y})\\ = tr(\frac{\partial f^{T}}{\partial \mathbf{Y}}d \mathbf{Y})\\ = tr(\frac{\partial f^{T}}{\partial \mathbf{Y}}d \mathbf{W}\mathbf{X}) \\ = tr(\mathbf{X}\frac{\partial f^{T}}{\partial \mathbf{Y}}d \mathbf{W})\\ = tr((\frac{\partial f}{\partial \mathbf{Y}}\mathbf{X}^{T})^{T}d \mathbf{W})\\ = tr(\frac{\partial f^{T}}{\partial \mathbf{W}}d \mathbf{W})

  \frac{\partial f}{\partial \mathbf{W}} =\frac{\partial f}{\partial \mathbf{Y}} \mathbf{X}^{T}

    

 

      

 

 

二.  矩阵对矩阵求导

若矩阵函数\mathbf{F}_{m\times n}对矩阵\mathbf{X}_{p\times q}  求导，则求导结果为\begin{bmatrix} \frac{\partial {F}_{1,1}}{\partial X_{1,1}} & \frac{\partial F_{1,2}}{\partial X_{1,1}} & \cdots & \frac{\partial F_{m,n}}{\partial X_{1,1}} \\ \frac{\partial F_{1,1}}{\partial X_{1,2}} & \frac{\partial F_{1,2}}{\partial X_{1,2}} & \cdots & \frac{\partial F_{m,n}}{\partial X_{1,2}} \\ \vdots & \vdots & \ddots \\ \vdots \frac{\partial F_{1,1}}{\partial X_{p,q}} & \frac{\partial F_{1,2}}{\partial X_{p,q}} & \cdots & \frac{\partial F_{m,n}}{\partial X_{p,q}} \\ \end{bmatrix}_{mn\times pq}, 其实就是\frac{\partial \mathbf{F}}{\partial \mathbf{X}} = \frac{\partial vec(\mathbf{F})}{\partial vec(\mathbf{X})}. 

vec是向量化运算，将矩阵按列优先展开，vec(\mathbf{X}) = [X_{1,1},X_{2,1},\cdots ,X_{p,1},\cdots , X_{1,q},\cdots ,X_{p,q}].

则矩阵微分d\mathbf{F} = \sum_{i=1}^{m}\sum_{j=1}^{n}\sum_{g=1}^{p}\sum_{k=1}^{q} \frac{\partial F_{i,j}}{\partial X_{g,k}} dX_{g,k}=\frac{\partial \mathbf{F}^{T}}{\partial \mathbf{X}}d\mathbf{X}

那么vec(d\mathbf{F}) = \frac{\partial \mathbf{F}^T}{\partial \mathbf{X}}vec(d\mathbf{X}).

那么，求矩阵对矩阵的导数就比较简单了。先对矩阵函数F求微分，将微分结果进行向量化运算，分离出vec(d\mathbf{X}),将其他项挪到左边。即可求出\frac{\partial \mathbf{F}}{\partial \mathbf{X}}. 这个过程和标量对矩阵求导十分相似。

在运算过程中涉及一些向量化运算和Kronecker积的运算，运算规则如下。

1. 向量化运算

 1）加减法  vec(\mathbf{A}\pm \mathbf{B}) = vec(\mathbf{A}) \pm vec(\mathbf{B})

 2） 向量乘法       vec(\boldsymbol{}{ab}^{T}) = \mathbf{b}\otimes \mathbf{a},  \bigotimes是 Kronecker积。

  3）  矩阵乘法      vec(\mathbf{AXB}) = \mathbf{B}^T\otimes \mathbf{A} vec(\mathbf{X})，\mathbf{A}_{m\times n},\mathbf{X}_{n\times p},\mathbf{B}_{p\times q}

                          证明如下：

                          \mathbf{X} = [\mathbf{x_{1}}, \cdots,\mathbf{x_{q}}], \mathbf{x_{i}}是p \times 1的向量。 \mathbf{e_{1}},\mathbf{\cdots,e_{q}},是单位矩阵I_{q\times q}的其中第i列。则\mathbf{X} = \sum_{i=1}^{q}\mathbf{x}_{i}\mathbf{e}_{i}^T

                          vec(AXB) = vec(A\sum_{i=1}^{q}x_{i}e_{i}^TB) \\\, \! = \sum_{i=1}^{q}vec(Ax_{i}e_{i}^TB) \\ =\sum_{i=1}^{q}vec((Ax_{i})(B^Te_{i})^T) \\ =\sum_{i=1}^{q}(B^{T}e_{i})\otimes (Ax_{i})\\ =( B^{T}\otimes A) \sum_{i=1}^{q}(e_{i}\otimes x_{i}) \\ =(B^{T}\otimes A)\sum_{i=1}^{q}vec(x_{i}e_{i}^{T}) \\ =(B^{T}\otimes A)vec(\sum_{i=1}^{q} x_{i}e_{i}^{T}) \\ \Lambda = (B^{T}\otimes A) vec(X)

    4）转置         vec(A^T) = K_{mn}vec(A),   K_{mn}  是一个 mn\times mn的交换矩阵，可以把按列优先展开的向量换成按行优先展开。

                         交换矩阵的特性：

                          K_{mn} = K_{nm}^{T} \\ K_{mn}K_{nm}=I

   5)  逐项乘法

        vec(A\odot B) = diag(A)vec(B),  diag(A)是一个mn \times mn对角矩阵，对角线上的元素依次为矩阵A的按列展开，其他元素为0

2.  Kronecker 积运算

   1）转置  (A\otimes B)^T = A^T\otimes B^T

   2)   交换

         K_{pm}( A\otimes B)K_{qn} = B\otimes A,  A是m*n的矩阵，B是p*q的矩阵

         证明：

                vec(AXB^T) = B\otimes A

                \\ vec(\mathbf{\mathbf{AXB}}^{T}) = (\mathbf{B}\otimes \mathbf{A}) vec(\mathbf{\mathbf{X}})= \mathbf{K}_{pm}vec((\mathbf{AXB}^{T})^{T}) = \mathbf{K}_{pm}vec(\mathbf{BX}^{T}\mathbf{A}^{T}) = \boldsymbol{K}_{pm}(\mathbf{A}\otimes \mathbf{B})vec(\mathbf{X}^{T}) = K_{pm}(\mathbf{A}\otimes \mathbf{B})\mathbf{K}_{nq}vec(\mathbf{X}) \\ \\ \mathbf{B}\otimes \mathbf{A}=\mathbf{K}_{pm}(\mathbf{A}\otimes \mathbf{B})\mathbf{K}_{qn}

 

 

 

 

 

 

                   

      

 

你可能感兴趣的:(数学基础)

  • 线性代数导引：张量与张量空间 AI大模型应用之禅 DeepSeekR1&AI大模型与大数据计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
    线性代数，张量，张量空间，深度学习，机器学习，人工智能1.背景介绍在现代人工智能领域，深度学习和机器学习算法的蓬勃发展，使得对数据的高效处理和表示能力提出了更高的要求。线性代数作为数学基础，为理解和构建这些算法提供了坚实的基础。而张量，作为一种高维数组的表示形式，成为了深度学习和机器学习的核心数据结构。本篇文章将从线性代数的角度出发，深入探讨张量与张量空间的概念，并阐述其在深度学习和机器学习中的重
  • 机器学习 - 学习线性模型的重要性 谦亨有终 跟着AI向前走机器学习学习人工智能
    在接下来的博文中，我们将重点学习线性模型的回归模型和分类模型，在学习之前，让我们来了解一下学习线性模型的重要性，以及如何入门学习。一、作为初学者如何学习线性模型？作为初学者，要高效学习机器学习以及其中的线性模型，可以遵循以下几个步骤和建议：（一）、机器学习的整体学习策略打好数学基础线性代数：理解向量、矩阵、线性变换等，这些是理解模型表示（如y=w^Tx+b）和算法优化的基础。微积分：掌握导数、梯度
  • 算法学习笔记之数学基础 threesevens 算法与数据结构算法
    例1（最小公倍数与最大公约数）计算最小公倍数公式：LCM(A,B)=A*B/GCD(A,B)A与B的最小公倍数等于A*B除以A与B的最大公约数计算最大公约数：辗转相除法原理：设A与B的最大公约数为x，则A是x的倍数，B也是x的倍数，令A=ax，B=bx，A/B取整为c，则A-cB=(a-bc)x。即A与B的余数也是x的倍数 intgcd(inta,intb) {   inttemp;   whil
  • 学习AI大模型用这十种方法，轻松入门 大模型玩家 学习人工智能transformer深度学习langchainagi大模型
    AI大模型学习在当前技术环境下，AI大模型学习不仅要求研究者具备深厚的数学基础和编程能力，还需要对特定领域的业务场景有深入的了解。通过不断优化模型结构和算法，AI大模型学习能够不断提升模型的准确性和效率，为人类生活和工作带来更多便利。系统化理论知识建构：对于AI大模型的学习，首要任务是对基础理论进行全面而深入的理解。这意味着需要投入大量的时间去研读经典的机器学习和深度学习教材，包括但不限于《统计学
  • 人工智能之数学基础：线性空间 每天五分钟玩转人工智能 机器学习深度学习之数学基础人工智能深度学习线性代数线性空间神经网络
    本文重点本文我们将讲解线性空间的知识，它不仅是数学中非常重要的知识点，它在机器学习和深度学习中的价值也是非常重要的，在机器学习和深度学习中是可以通过线性空间来进行解释的。线性空间的直观理解线性空间可以看作是一个多维的“宇宙”，其中的“点”由向量表示，而“运动”则通过向量的加法和数乘来实现。这个宇宙中的每一个向量都可以看作是从原点出发到该点的一条有向线段，而线性空间的维度则决定了这个宇宙的大小和复杂
  • 用大模型学大模型02-数学基础 微积分 wyg_031113 人工智能
    https://metaso.cn/s/uxPBB9C我正在学习深度学习相关的数学知识,学到了微积分核心概念：导数（尤其是偏导数）、梯度、链式法则；积分与最优化（如梯度下降法的数学推导）给我一个入门级的完整教程和实例好吧，我现在需要帮用户整理一个关于深度学习中微积分核心概念的入门教程和实例。用户提到了导数、偏导数、梯度、链式法则，还有积分和优化比如梯度下降法。我得先理清楚这些概念之间的联系，然后结
  • 用大模型学大模型03-数学基础 概率论 wyg_031113 概率论人工智能
    https://metaso.cn/s/Jp0OU9w提示词:我正在学习深度学习相关的数学知识，学到了概率论与统计学部分，给我一个入门级的完整教程和实例。好的，我现在需要回答用户关于深度学习所需的概率论与统计学入门教程和实例的问题。用户希望得到一个完整的教程和实例，所以我要从我搜索到的资料中整理出相关的知识点和学习路径，并结合实例说明。首先，查看证据中的相关内容。提到花书学习笔记，涵盖了概率论、信
  • 机器学习数学基础：21.特征值与特征向量 @心都 机器学习概率论人工智能
    一、引言在现代科学与工程的众多领域中，线性代数扮演着举足轻重的角色。其中，特征值、特征向量以及相似对角化的概念和方法，不仅是线性代数理论体系的核心部分，更是解决实际问题的有力工具。无论是在物理学中描述系统的振动模式，还是在计算机科学里进行数据降维与图像处理，它们都发挥着关键作用。本教程将深入且全面地对这些内容展开讲解，旨在帮助读者透彻理解并熟练运用相关知识。二、基础知识准备（一）对角矩阵的高次幂计
  • 分布式训练三大并行策略：数据、模型与流水线并行的本质解析 WHCIS #分布式训练人工智能与机器学习分布式人工智能深度学习
    截至2023年，大型语言模型的参数量已突破万亿级别（如GooglePaLM2达到3400亿参数），单卡显存容量（NVIDIAA10080GB）与计算能力（312TFLOPS）面临严峻挑战。分布式训练通过多维度并行策略实现：算力维度：聚合多卡计算能力存储维度：分布式参数存储通信维度：优化数据传输路径本文将深入剖析三大并行策略的数学本质。一、数据并行：分布式优化的数学基础1.1同步SGD的收敛性证明定
  • 书籍-《信息科学的数学基础》 机器学习人工智能数学
    书籍：MathematicalFoundationsofInformationSciences作者：EsfandiarHaghverdi，LiugenZhu出版：WorldScientificPublishingCompany编辑：陈萍萍的公主@一点人工一点智能下载：书籍下载-《信息科学的数学基础》01书籍介绍这是一本简明扼要的书籍，旨在引导学生进入逻辑思维的基本原理和重要的数学结构的世界。这些知
  • 书籍-《机器学习数学基础》 机器学习深度学习数学
    书籍：MathematicsforMachineLearning作者：MarcPeterDeisenroth，A.AldoFaisal，ChengSoonOng出版：CambridgeUniversityPress编辑：陈萍萍的公主@一点人工一点智能下载：书籍下载-《机器学习数学基础》01书籍介绍理解机器学习所需的基本数学工具包括线性代数、解析几何、矩阵分解、向量微积分、最优化、概率论和统计学。这
  • 书籍-《强化学习数学基础》 强化学习数学人工智能
    书籍：MathematicalFoundationsofReinforcementLearning作者：赵世钰出版：Springer编辑：陈萍萍的公主@一点人工一点智能下载：书籍下载-《强化学习数学基础》01书籍介绍本书对基本概念、核心挑战和经典强化学习算法进行了数学但易于理解的介绍。它旨在帮助读者理解算法的理论基础，提供对其设计和功能的见解。整个过程中包括许多说明性示例。数学内容经过精心设计，以
  • 初学者怎么入门大语言模型（LLM） 大模型
    大语言模型（LLM）作为人工智能（AI）领域的核心技术之一，近年来受到了广泛的关注。对于初学者来说，入门LLM并非难事，但需要从理论学习、数学基础到实践操作逐步深入。掌握基础数学与编程技能，理解自然语言处理的相关概念，以及熟悉LLM的架构和应用，将为学习者铺平入门的道路。下面我们就来详细探讨如何从零开始入门大语言模型。一、了解大语言模型（LLM）的基本概念大语言模型（LLM）是通过海量文本数据进行
  • AGI方向研究 微醺欧耶 agi
    要成为一名合格的AGI（通用人工智能）实习生，你需要具备跨学科的知识体系、扎实的技术能力以及前沿研究视野。以下是基于你当前基础的能力扩展方向、关键研究领域以及未来发展的详细分析：---###**一、AGI实习生需具备的核心能力**####1.**数学与理论基础**-**数学基础**：线性代数（矩阵运算、特征值）、概率统计（贝叶斯理论、分布模型）、微积分（梯度优化）、信息论（熵、KL散度）。-**计
  • OSG学习笔记 - 数学基础（1） 听风者868 OSGc++图形学其他学习opengl
    1、OSG数学基础OSG采用的世界坐标系是左手坐标系，这一点与OpenGL保持一样的，但坐标轴的方向不一样。·OSG的X轴向右，Y轴朝里，Z轴向上。·OpenGL的X轴向右，Y轴向上，Z轴朝外。1.1世界坐标系-物体坐标系转换世界坐标系-物理坐标系描述的问题主要是关于物体本身的。osg::PositionAttitudeTransform//位置变换类osg::MatrixTransform//矩
  • AI学习专题（一）LLM技术路线 王钧石的技术博客 大模型人工智能学习ai
    阶段1：AI及大模型基础（1-2个月）数学基础线性代数（矩阵、特征值分解、SVD）概率论与统计（贝叶斯定理、极大似然估计）最优化方法（梯度下降、拉格朗日乘子法）编程&框架Python（NumPy、Pandas、Matplotlib）PyTorch&TensorFlow基础HuggingFaceTransformers入门深度学习基础机器学习基础（监督/无监督学习、正则化、过拟合）反向传播、优化器（
  • 深度学习-数学基础-01 神经网络深度学习
    下面的内容是豆包总结的。学习神经网络需要以下数学基础：线性代数向量与矩阵神经网络中的数据通常以向量（如输入特征向量）和矩阵（如权重矩阵）的形式表示。理解向量的点积、加法、减法等运算，以及矩阵的乘法、转置等操作至关重要。例如，在一个简单的全连接神经网络中，输入层到隐藏层的计算就是通过输入向量与权重矩阵相乘来实现的。矩阵的秩、特征值和特征向量的概念在神经网络的一些高级主题如主成分分析（PCA）降维和深
  • 机器学习数学基础：20.方程组解的结构 @心都 机器学习数学基础机器学习人工智能
    一、教程简介本教程专门为线性代数零基础的小白打造，旨在全面且细致地讲解解方程组与基础解系的相关知识，助力大家逐步扎实地掌握这一重要内容板块。二、知识目标透彻理解非齐次与齐次线性方程组的定义、本质区别以及对应的解法。熟练掌握判断方程组解的存在性的方法，精准把握秩在其中起到的决定性作用。能够独立且准确地求解齐次线性方程组，并规范地表示出其通解。精通判断一个向量组是否为齐次线性方程组的基础解系的方法，并
  • 机器学习数学基础：18.向量组及其线性组合 @心都 机器学习数学基础机器学习概率论线性代数
    向量组与线性表示：案例与教程详解一、基础概念（一）向量组向量组是若干同位数列向量组成的集合。比如在平面直角坐标系中，向量组{α⃗1=[10],α⃗2=[01]}\{\vec{\alpha}_1\=\begin{bmatrix}1\\0\end{bmatrix},\vec{\alpha}_2\=\begin{bmatrix}0\\1\end{bmatrix}\}{α1=[10],α2=[01]}，这
  • 机器学习数学基础：8.泰勒公式 @心都 机器学习数学基础机器学习人工智能
    一、泰勒公式的由来：为啥我们需要它？同学们，想象一下，你拿到了一块超级复杂、弯弯曲曲，就像一团乱麻似的拼图（假设这拼图代表一个复杂函数，比如一条有各种起伏的波浪线），而你手头只有一些简单的积木块（这里的积木块就是多项式啦），现在要你用这些简单积木拼出拼图的模样，是不是感觉无从下手？这时候，泰勒公式就像一位智慧的导师闪亮登场，它会告诉你：“别慌，孩子，我来教你怎么挑选积木块，怎么决定它们的形状和大小
  • 机器学习数学基础：3.偏导数 @心都 机器学习数学基础机器学习人工智能
    偏导数教程一、偏导数的引入在我们研究一元函数y=f(x)y=f(x)y=f(x)时，导数y′=f′(x)y^\prime=f^\prime(x)y′=f′(x)表示函数yyy关于xxx的变化率。然而，当我们遇到多元函数，例如二元函数z=f(x,y)z=f(x,y)z=f(x,y)时，情况变得更加复杂。我们可能会想知道函数zzz在xxx方向或yyy方向上的变化率，这就引入了偏导数的概念。二、偏导数的
  • 机器学习数学基础：2.连续性与导数 @心都 机器学习数学基础机器学习概率论人工智能
    函数连续性、瞬时速度、导数相关知识一、函数连续性（一）函数在某点连续的条件有定义：函数在点x0x_0x0处要有明确、确定的值f(x0)f(x_0)f(x0)。例如，f(x)=1xf(x)=\frac{1}{x}f(x)=x1在x=0x=0x=0处无定义，不满足此条件，所以在x=0x=0x=0处不连续。极限存在：当xxx从x0x_0x0左侧（x→x0−x\tox_0^{-}x→x0−）和右侧（x→x
  • 机器学习数学基础：19.线性相关与线性无关 @心都 机器学习数学基础机器学习概率论线性代数
    一、线性相关与线性无关的定义（一）线性相关想象我们有一组向量，就好比是一群有着不同“力量”和“方向”的小伙伴。给定的向量组α⃗1,α⃗2,⋯ ,α⃗m\vec{\alpha}_1,\vec{\alpha}_2,\cdots,\vec{\alpha}_mα1,α2,⋯,αm，如果能找到不全为零的数k1,k2,⋯ ,kmk_1,k_2,\cdots,k_mk1,k2,⋯,km，让k1α⃗1+k2α⃗2
  • 机器学习数学基础：14.矩阵的公式 @心都 机器学习数学基础机器学习矩阵人工智能
    1.操作顺序可交换对于矩阵AAA，若存在两种运算???和???，使得(A?)?=(A?)?(A^{?})^{?}\=(A^{?})^{?}(A?)?=(A?)?，这意味着这两种运算的顺序可以交换。由此我们得到以下三个重要等式：(A∗)−1=(A−1)∗(A^{*})^{-1}\=(A^{-1})^{*}(A∗)−1=(A−1)∗：已知伴随矩阵与逆矩阵的关系A∗=∣A∣A−1A^{*}\=|A|A^
  • 【AI原理解析】— Gemini模型 coolkidlan AI学习路径AIGC人工智能AIGC
    目录1.模型概述定义特点2.模型基础与架构模型架构模型尺寸3.多模态处理能力输入处理数据处理训练过程4.技术细节与优化预训练上下文长度注意机制5.安全性与编程能力安全性评估编程能力6.模型发布与应用发布时间应用方向7.性能评估8.数学基础8.1Transformer解码器基础8.1.1自注意力机制（Self-Attention）8.1.2前馈神经网络（Feed-ForwardNeuralNetwo
  • 机器学习数学基础：11.行列式的多种计算方法 @心都 机器学习数学基础机器学习线性代数人工智能
    行列式的多种计算方法行（列）相等型对于行列式∣1+a11122+a22333+a34444+a∣\begin{vmatrix}1+a&1&1&1\\2&2+a&2&2\\3&3&3+a&3\\4&4&4&4+a\end{vmatrix}1+a23412+a34123+a41234+a，通过将第一行元素都变为10+a10+a10+a，得到∣10+a10+a10+a10+a22+a22333+a344
  • 自动驾驶领域成长方案 树上求索 自动驾驶人工智能机器学习
    一、学习目标成为自动驾驶领域专家，全面掌握自动驾驶技术体系，能独立进行自动驾驶系统设计、开发与优化，解决实际工程问题。二、成长阶段（一）基础理论奠基期（1-2年）专业知识学习：学习数学（高等数学、线性代数、概率论与数理统计、数值分析等），为理解算法和模型提供数学基础；深入研究自动驾驶涉及的专业课程，如控制理论、传感器原理（激光雷达、摄像头、毫米波雷达等）、机器学习（监督学习、无监督学习、深度学习）
  • 深度学习篇---深度学习相关知识点&关键名词含义 Ronin-Lotus 深度学习篇深度学习人工智能机器学习pytorchpaddlepaddlepython
    文章目录前言第一部分:相关知识点一、基础铺垫层（必须掌握的核心基础）1.数学基础•线性代数•微积分•概率与统计2.编程基础3.机器学习基础二、深度学习核心层（神经网络与训练机制）1.神经网络基础2.激活函数（ActivationFunction）3.损失函数（LossFunction）4.优化算法（Optimization）5.反向传播（Backpropagation）6.正则化与调优三、进阶模型
  • 为什么关系模型不叫表模型 昊昊该干饭了 mysqlIT知识数据库oraclemysql
    在数据库设计中，关系模型（RelationalModel）是最广泛应用的模型之一。然而，许多初学者容易将其简单地理解为"表模型"，因为在实际应用中，数据通常以表的形式存储和展示。那么，为什么关系模型不被直接称为"表模型"呢？本篇文章将从数学基础、逻辑与物理实现、数据库完整性、数据独立性及查询操作等多个角度，深入剖析关系模型的本质，并解释它为何不同于一个简单的表结构。目录1.关系模型的数学基础1.1
  • 区块链的数学基础：核心原理与应用解析 silver687 区块链
    区块链技术的核心原理和应用离不开其强大的数学基础，以下是对其数学基础、核心原理与应用的详细解析：区块链的数学基础区块链的数学基础主要包括以下几个核心领域：1.密码学：密码学是区块链安全性的基石，主要保障数据的机密性、完整性和不可抵赖性。其中，对称加密算法（如AES）加密和解密使用相同密钥，计算效率高，但不适用于区块链的公开网络环境；非对称加密使用一对密钥（公钥和私钥），用户通过私钥签名交易，其他人
  • [星球大战]阿纳金的背叛 comsci
          本来杰迪圣殿的长老是不同意让阿纳金接受训练的.........     但是由于政治原因,长老会妥协了...这给邪恶的力量带来了机会     所以......现代的地球联邦接受了这个教训...绝对不让某些年轻人进入学院    
  • 看懂它，你就可以任性的玩耍了！ aijuans JavaScript
              javascript作为前端开发的标配技能，如果不掌握好它的三大特点：1.原型 2.作用域 3. 闭包 ,又怎么可以说你学好了这门语言呢？如果标配的技能都没有撑握好，怎么可以任性的玩耍呢？怎么验证自己学好了以上三个基本点呢，我找到一段不错的代码，稍加改动，如果能够读懂它，那么你就可以任性了。 function jClass(b
  • Java常用工具包 Jodd Kai_Ge javajodd
    Jodd 是一个开源的 Java 工具集， 包含一些实用的工具类和小型框架。简单，却很强大！ 写道 Jodd = Tools + IoC + MVC + DB + AOP + TX + JSON + HTML < 1.5 Mb Jodd 被分成众多模块，按需选择，其中 工具类模块有： jodd-core    &nb
  • SpringMvc下载 120153216 springMVC
    @RequestMapping(value = WebUrlConstant.DOWNLOAD) public void download(HttpServletRequest request,HttpServletResponse response,String fileName) { OutputStream os = null; InputStream is = null;
  • Python 标准异常总结 2002wmj python
    Python标准异常总结 AssertionError 断言语句（assert）失败 AttributeError 尝试访问未知的对象属性 EOFError 用户输入文件末尾标志EOF（Ctrl+d） FloatingPointError 浮点计算错误 GeneratorExit generator.close()方法被调用的时候 ImportError 导入模块失
  • SQL函数返回临时表结构的数据用于查询 357029540 SQL Server
    这两天在做一个查询的SQL，这个SQL的一个条件是通过游标实现另外两张表查询出一个多条数据，这些数据都是INT类型，然后用IN条件进行查询，并且查询这两张表需要通过外部传入参数才能查询出所需数据，于是想到了用SQL函数返回值，并且也这样做了，由于是返回多条数据，所以把查询出来的INT类型值都拼接为了字符串，这时就遇到问题了，在查询SQL中因为条件是INT值，SQL函数的CAST和CONVERST都
  • java 时间格式化 | 比较大小| 时区 个人笔记 7454103 javaeclipsetomcatcMyEclipse
    个人总结！ 不当之处多多包含！ 引用 1.0 如何设置 tomcat 的时区：          位置：(catalina.bat---JAVA_OPTS  下面加上)          set JAVA_OPT
  • 时间获取Clander的用法 adminjun Clander时间
    /**    * 得到几天前的时间    * @param d    * @param day    * @return    */   public static Date getDateBefore(Date d,int day){    Calend
  • JVM初探与设置 aijuans java
    JVM是Java Virtual Machine（Java虚拟机）的缩写，JVM是一种用于计算设备的规范，它是一个虚构出来的计算机，是通过在实际的计算机上仿真模拟各种计算机功能来实现的。Java虚拟机包括一套字节码指令集、一组寄存器、一个栈、一个垃圾回收堆和一个存储方法域。 JVM屏蔽了与具体操作系统平台相关的信息，使Java程序只需生成在Java虚拟机上运行的目标代码（字节码）,就可以在多种平台
  • SQL中ON和WHERE的区别 avords
    SQL中ON和WHERE的区别   数据库在通过连接两张或多张表来返回记录时，都会生成一张中间的临时表，然后再将这张临时表返回给用户。   www.2cto.com   在使用left jion时，on和where条件的区别如下：  1、 on条件是在生成临时表时使用的条件，它不管on中的条件是否为真，都会返回左边表中的记录。 
  • 说说自信 houxinyou 工作生活
    自信的来源分为两种,一种是源于实力,一种源于头脑.实力是一个综合的评定,有自身的能力,能利用的资源等.比如我想去月亮上,要身体素质过硬,还要有飞船等等一系列的东西.这些都属于实力的一部分.而头脑不同,只要你头脑够简单就可以了!同样要上月亮上,你想,我一跳,1米,我多跳几下,跳个几年,应该就到了!什么?你说我会往下掉?你笨呀你!找个东西踩一下不就行了吗?     无论工作还
  • WEBLOGIC事务超时设置 bijian1013 weblogicjta事务超时
            系统中统计数据，由于调用统计过程，执行时间超过了weblogic设置的时间，提示如下错误： 统计数据出错! 原因：The transaction is no longer active - status: 'Rolling Back. [Reason=weblogic.transaction.internal
  • 两年已过去，再看该如何快速融入新团队 bingyingao java互联网融入架构新团队
    偶得的空闲，翻到了两年前的帖子 该如何快速融入一个新团队，有所感触，就记下来，为下一个两年后的今天做参考。     时隔两年半之后的今天，再来看当初的这个博客，别有一番滋味。而我已经于今年三月份离开了当初所在的团队，加入另外的一个项目组，2011年的这篇博客之后的时光，我很好的融入了那个团队，而直到现在和同事们关系都特别好。大家在短短一年半的时间离一起经历了一
  • 【Spark七十七】Spark分析Nginx和Apache的access.log bit1129 apache
    Spark分析Nginx和Apache的access.log，第一个问题是要对Nginx和Apache的access.log文件进行按行解析，按行解析就的方法是正则表达式：   Nginx的access.log解析正则表达式   val PATTERN = """([^ ]*) ([^ ]*) ([^ ]*) (\\[.*\\]) (\&q
  • Erlang patch bookjovi erlang
    Totally five patchs committed to erlang otp, just small patchs. IMO, erlang really is a interesting programming language, I really like its concurrency feature. but the functional programming style
  • log4j日志路径中加入日期 bro_feng javalog4j
    要用log4j使用记录日志，日志路径有每日的日期，文件大小5M新增文件。 实现方式 log4j: <appender name="serviceLog" class="org.apache.log4j.RollingFileAppender"> <param name="Encoding" v
  • 读《研磨设计模式》-代码笔记-桥接模式 bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ /** * 个人觉得关于桥接模式的例子，蜡笔和毛笔这个例子是最贴切的：http://www.cnblogs.com/zhenyulu/articles/67016.html * 笔和颜色是可分离的，蜡笔把两者耦合在一起了：一支蜡笔只有一种
  • windows7下SVN和Eclipse插件安装 chenyu19891124 eclipse插件
    今天花了一天时间弄SVN和Eclipse插件的安装，今天弄好了。svn插件和Eclipse整合有两种方式，一种是直接下载插件包，二种是通过Eclipse在线更新。由于之前Eclipse版本和svn插件版本有差别，始终是没装上。最后在网上找到了适合的版本。所用的环境系统：windows7JDK：1.7svn插件包版本：1.8.16Eclipse：3.7.2工具下载地址：Eclipse下在地址：htt
  • [转帖]工作流引擎设计思路 comsci 设计模式工作应用服务器workflow企业应用
    作为国内的同行，我非常希望在流程设计方面和大家交流，刚发现篇好文(那么好的文章，现在才发现，可惜)，关于流程设计的一些原理，个人觉得本文站得高，看得远，比俺的文章有深度，转载如下 ================================================================================= 自开博以来不断有朋友来探讨工作流引擎该如何
  • Linux 查看内存，CPU及硬盘大小的方法 daizj linuxcpu内存硬盘大小
    一、查看CPU信息的命令 [root@R4 ~]# cat /proc/cpuinfo |grep "model name" && cat /proc/cpuinfo |grep "physical id" model name : Intel(R) Xeon(R) CPU X5450 @ 3.00GHz model name :
  • linux 踢出在线用户 dongwei_6688 linux
    两个步骤： 1.用w命令找到要踢出的用户，比如下面：   [root@localhost ~]# w 18:16:55 up 39 days, 8:27, 3 users, load average: 0.03, 0.03, 0.00 USER TTY FROM LOGIN@ IDLE JCPU PCPU WHAT
  • 放手吧,就像不曾拥有过一样 dcj3sjt126com
    内容提要： 静悠悠编著的《放手吧就像不曾拥有过一样》集结“全球华语世界最舒缓心灵”的精华故事，触碰生命最深层次的感动，献给全世界亿万读者。《放手吧就像不曾拥有过一样》的作者衷心地祝愿每一位读者都给自己一个重新出发的理由，将那些令你痛苦的、扛起的、背负的，一并都放下吧！把憔悴的面容换做一种清淡的微笑，把沉重的步伐调节成春天五线谱上的音符，让自己踏着轻快的节奏，在人生的海面上悠然漂荡，享受宁静与
  • php二进制安全的含义 dcj3sjt126com PHP
    PHP里，有string的概念。 string里，每个字符的大小为byte（与PHP相比，Java的每个字符为Character，是UTF8字符，C语言的每个字符可以在编译时选择）。 byte里，有ASCII代码的字符，例如ABC，123，abc，也有一些特殊字符，例如回车，退格之类的。 特殊字符很多是不能显示的。或者说，他们的显示方式没有标准，例如编码65到哪儿都是字母A，编码97到哪儿都是字符
  • Linux下禁用T440s，X240的一体化触摸板(touchpad) gashero linuxThinkPad触摸板
    自打1月买了Thinkpad T440s就一直很火大，其中最让人恼火的莫过于触摸板。   Thinkpad的经典就包括用了小红点(TrackPoint)。但是小红点只能定位，还是需要鼠标的左右键的。但是自打T440s等开始启用了一体化触摸板，不再有实体的按键了。问题是要是好用也行。   实际使用中，触摸板一堆问题，比如定位有抖动，以及按键时会有飘逸。这就导致了单击经常就
  • graph_dfs hcx2013 Graph
    package edu.xidian.graph; class MyStack { private final int SIZE = 20; private int[] st; private int top; public MyStack() { st = new int[SIZE]; top = -1; } public void push(i
  • Spring4.1新特性——Spring核心部分及其他 jinnianshilongnian spring 4.1
    目录 Spring4.1新特性——综述 Spring4.1新特性——Spring核心部分及其他 Spring4.1新特性——Spring缓存框架增强 Spring4.1新特性——异步调用和事件机制的异常处理 Spring4.1新特性——数据库集成测试脚本初始化 Spring4.1新特性——Spring MVC增强 Spring4.1新特性——页面自动化测试框架Spring MVC T
  • 配置HiveServer2的安全策略之自定义用户名密码验证 liyonghui160com
        具体从网上看   http://doc.mapr.com/display/MapR/Using+HiveServer2#UsingHiveServer2-ConfiguringCustomAuthentication   LDAP Authentication using OpenLDAP Setting
  • 一位30多的程序员生涯经验总结 pda158 编程工作生活咨询
    1.客户在接触到产品之后，才会真正明白自己的需求。 　　这是我在我的第一份工作上面学来的。只有当我们给客户展示产品的时候，他们才会意识到哪些是必须的。给出一个功能性原型设计远远比一张长长的文字表格要好。 2.只要有充足的时间，所有安全防御系统都将失败。 　　安全防御现如今是全世界都在关注的大课题、大挑战。我们必须时时刻刻积极完善它，因为黑客只要有一次成功，就可以彻底打败你。   3.
  • 分布式web服务架构的演变 自由的奴隶 linuxWeb应用服务器互联网
    最开始，由于某些想法，于是在互联网上搭建了一个网站，这个时候甚至有可能主机都是租借的，但由于这篇文章我们只关注架构的演变历程，因此就假设这个时候已经是托管了一台主机，并且有一定的带宽了，这个时候由于网站具备了一定的特色，吸引了部分人访问，逐渐你发现系统的压力越来越高，响应速度越来越慢，而这个时候比较明显的是数据库和应用互相影响，应用出问题了，数据库也很容易出现问题，而数据库出问题的时候，应用也容易
  • 初探Druid连接池之二——慢SQL日志记录 xingsan_zhang 日志连接池druid慢SQL
    由于工作原因，这里先不说连接数据库部分的配置，后面会补上，直接进入慢SQL日志记录。   1.applicationContext.xml中增加如下配置： <bean abstract="true" id="mysql_database" class="com.alibaba.druid.pool.DruidDataSourc
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他