QANet 论文笔记
QANet 论文笔记
文章目录
- QANet 论文笔记
- 摘要
- 简介
- 模型
- 1. Input embedding layer
- word embedding
- character embedding
- 2. Embedding encoder layer
- (1) position encoding
- (2) depthwise separable convolutions
- (3) self-attention
- (4) feed-forward
- 3. Context-Query attention layer
- 4. Model encoder layer
- 5. Output layer
- 参考文献
QANet: Combining Local Convolution With Global Self-Attention For Reading Comprehension
卷积+自注意力
摘要
目前的端到端机器阅读和问答模型主要基于包含注意力的循环神经网络,主要缺点:在训练和推理方面效率较低。
我们提出了一种名为QANet的问答架构,它的编码器仅由卷积和自注意力(self-attention)组成,其中,卷积对局部交互和自注意力模型的全局交互进行建模。
效果:在SQuAD数据集中,我们模型的训练速度提高了3至13倍,推理速度提高了4至9倍,同时达到了与循环模型相媲美精确度。加速增益(speed-up gain)使我们能够用更多的数据来训练模型。因此,我们将我们的模型,与由神经机器翻译模型的反向翻译生成的数据结合起来。在SQuAD数据集上,我们使用增强数据训练的单一模型在测试集中F1值达到 84.6,这显著优于过去公布的F1最佳值81.8。
简介
在过去几年中最成功的模型通常采用了两项关键要技术:(1)处理顺序输入的循环模型(2)应对长期交互的注意力要素。Seo等人于2016年提出的的双向注意力流(Bidirectional Attention Flow,BiDAF)模型将这两项要素成功地结合在了一起,该模型在SQuAD数据集上取得了显著的效果。这些模型的一个缺点是,它们的循环特性使得它们在训练和推理方面的效率通常较低,特别是对于长文本而言。昂贵的训练不仅会导致实验的周期延长,限制研究人员进行快速迭代,还会使模型难以被用于更大的数据集中。与此同时,缓慢的推理速度阻碍了机器理解系统在实时应用中的部署。
在本文中,为了使机器理解更高效,我们提出去掉这些模型的循环性质,仅将卷积和自注意力作为编码器的构成模块,分别对问题和语境进行编码。然后,我们通过标准注意力(standard attentions,Xiong等人于2016年提出;Seo 等人于2016年提出;Bahdanau等人于2015年提出)来学习语境和问题之间的交互。在最终对每个作为答案范围的开始或结束位置的概率进行解码之前,用我们的无循环编码器再次对结果表征进行编码。我们将该架构称为QANet。
模型设计的主要思想:卷积捕获文本的局部结构,而自注意力则学习每对单词之间的全局交互。附加语境疑问注意力(the additional context-query attention)是一个标准模块,用于为语境段落中的每个位置构造查询感知的语境向量(query-aware context vector),这在随后的建模层中得到使用。我们的架构的前馈特性极大地提高了模型的效率。在基于SQuAD数据集的实验中,我们模型的训练速度提高了3至13倍,推理速度提高了4至9倍。作一个简单的比较,我们的模型可以在3个小时的训练中达到与BiDAF模型(Seo等人于2016年提出)相同的精确度(F1值为77.0),在此之前,这一过程需花费15个小时的时间。加速增益还允许我们使用更多的迭代来训练模型,以获得比竞争模型更好的结果。例如,如果我们允许我们的模型进行18个小时的训练,它在开发集(dev set)上的F1值达到了82.7,这比Seo等人于 2016年提出的模型,表现得要好很多,并且与已发布过的最佳结果相媲美。
模型
模型共有五部分:
- Input embedding layer
- Embedding encoder layer
- Context-query attention layer
- Model encoder layer
- Output layer
下面分层说明模型的各部分
1. Input embedding layer
输入嵌入包括word embedding + character embedding,即词嵌入和字符嵌入。
word embedding
p 1 p_1 p1=300维。
采用预训练的glove词向量。在训练时固定不变。对于词典中未出现的新词,map到< UNK >这个token,随机初始化,这个向量是可训练的。
character embedding
p 2 p_2 p2=200维(每个字符)。是可训练的。
每个词可以表示为字符的拼接,每个单词被截断或者pad到长度16。
取这个矩阵每行的最大值作为该词的固定长度表示。(池化)
最终一个单词表示为二者的拼接: [ x w ; x c ] ∈ R p 1 + p 2 [x_w; x_c] \in \mathbb{R}^{p_1+p_2} [xw;xc]∈Rp1+p2
x c x_c xc:词嵌入 x c x_c xc:字符嵌入的卷积输出。
在这之后加2层highway network
highway network:
y = H ( x , W H ) ∗ T ( x , W T ) + x ∗ ( 1 − T ( x , W T ) ) y=H(x,W_H)*T(x,W_T)+x*(1-T(x,W_T)) y=H(x,WH)∗T(x,WT)+x∗(1−T(x,WT))
H:非线性变换函数; T:transform gate; 1-T:C,carry gate。
2. Embedding encoder layer
编码层是对基本块的堆叠
基本块:position encoding + convolution layer ×# + self-attention layer + feed-forward layer,如上图右半部分所示。
该层只用了一个编码块(基本块)。
参数设置如下:
kernel size=7,filter个数d=128,卷积层数n=4,self-attention heads数h=8。
每个子层都采用残差结构。
输入是p1+p2=500,一维卷积到d=128,输出维度也是128。
(1) position encoding
直接采用公式计算。与Attention is all you need论文中相同。
{ P E 2 i ( p ) = sin ( p / 1000 0 2 i / d p o s ) P E 2 i + 1 ( p ) = cos ( p / 1000 0 2 i / d p o s ) \left\{ \begin{aligned} PE_{2i}(p)=\sin(p/10000^{2i/d_{pos}}) \\ PE_{2i+1}(p)=\cos(p/10000^{2i/d_{pos}}) \\ \end{aligned} \right. {PE2i(p)=sin(p/100002i/dpos)PE2i+1(p)=cos(p/100002i/dpos)
(2) depthwise separable convolutions
论文中提到,该卷积方式比普通的卷积参数更少,泛化能力更强。它的核心思想是将一个完整的卷积运算分解为 depthwise convolution 和 pointwise convolution 两个步骤。
我们举个例子:
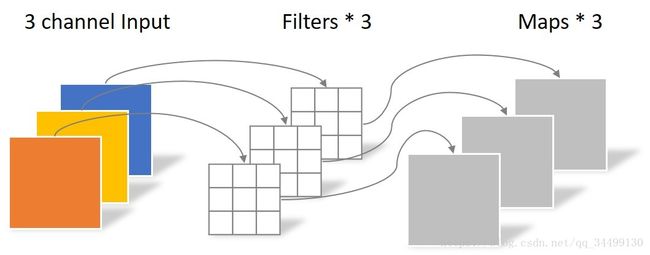
首先是depthwise convolution,以上图为例,假设输入是6464的3通道图片,使用33*1大小的卷积核,filter 数量等于上一层的depth,对输入的每个 channel 独立进行卷积运算,得到与上层depth相同个数的feature map。对应到图里即3个filter分别对3个channel进行卷积,得到3个feature map。
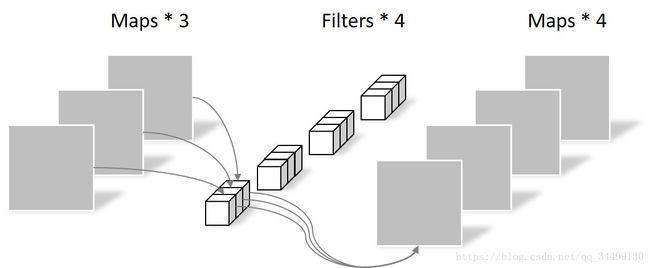
然后是pointwise convolution,和常规卷积运算类似,卷积核的尺寸为 1×1×M,M等于上一层的depth。它会将上一步的feature map在深度方向上进行加权组合,生成新的feature map,有几个filter就有几个feature map。如图3所示,输入depth为3,卷积核大小为113,使用4个filter,最终生成4个feature map。
假设每个channel的depth=1该模型的参数数量为:3313+1134=39;普通卷积需要四个333的filter,参数数量为333*4=108。
(3) self-attention
参考另一篇博客Attention Is All You Need 论文笔记
(4) feed-forward
全连接的前向神经网络
3. Context-Query attention layer
Attention:
A t t e n t i o n ( Q , K , V ) = S o f t m a x ( S i m i l a r i t y ( Q , K ) ) ∗ V Attention(Q,K,V)=Softmax(Similarity(Q,K))*V Attention(Q,K,V)=Softmax(Similarity(Q,K))∗V
相似度常用的计算方法有点积、拼接、感知机等。(BERT、Transformer用点积)
一般的attention是k=v,self-attention中q=k=v。
本文中:
用C表示编码后的context,Q表示编码后的query。 C ∈ R d ∗ n , Q ∈ R n ∗ m C\in \mathbb{R}^{d*n}, Q\in \mathbb{R}^{n*m} C∈Rd∗n,Q∈Rn∗m
- 先计算context与query的相似度 S , S ∈ R n ∗ m S, S\in \mathbb{R}^{n*m} S,S∈Rn∗m。S: f ( q , c ) = W 0 [ q , c , q ⊙ c ] f(q,c)=W_0[q,c,q\odot c] f(q,c)=W0[q,c,q⊙c],其中 ⊙ \odot ⊙表示按位乘, W 0 W_0 W0是可训练的变量。
- 用softmax对S的行、列分别归一化得 S ˉ \bar S Sˉ, S ˉ ˉ \bar{\bar S} Sˉˉ,则context-to-query attention矩阵 A = S ˉ ⋅ Q ∈ R n ∗ m A=\bar S\cdot Q \in \mathbb{R}^{n*m} A=Sˉ⋅Q∈Rn∗m,query-to-contxt attention矩阵 B = S ˉ ⋅ S ˉ ˉ ⋅ C T ∈ R n ∗ d B=\bar S\cdot \bar{\bar S}\cdot C^T \in \mathbb{R}^{n*d} B=Sˉ⋅Sˉˉ⋅CT∈Rn∗d (参考DCN)
4. Model encoder layer
共有三个model encoder block连接,每个model encoder block由7个encoder block堆叠而成。3个model encoder block之间共享参数。
与BIDAF类似,每个位置输入是 [ c , a , c ⊙ a , c ⊙ b ] [c,a,c\odot a,c\odot b] [c,a,c⊙a,c⊙b]
a,b分别是A,B的行,c是context对应位置的单词中间表示。
5. Output layer
该层具体视任务而定。
在SQuAD(stanford question answering dataset)任务上:
分别预测每个位置是answer span的起始点和结束点的概率,分别记为 p 1 p^1 p1, p w p^w pw
p 1 = S o f t m a x ( W 1 [ M 0 ; M 1 ] ) p^1=Softmax(W_1[M_0;M_1]) p1=Softmax(W1[M0;M1])
p 2 = S o f t m a x ( W 2 [ M 0 ; M 2 ] ) p^2=Softmax(W_2[M_0;M_2]) p2=Softmax(W2[M0;M2])
其中 W 1 W_1 W1, W 2 W_2 W2是可训练变量, M 0 M_0 M0, M 1 M_1 M1, M 2 M_2 M2,对应三个model encoder block输出(自底向上)。
目标函数:
L ( θ ) = − 1 N ∑ i N [ log ( p y i 1 1 ) + log ( p y i 2 2 ) ] L(\theta)=-\frac{1}{N}\sum^N_i[\log(p^1_{y_i^1})+\log(p^2_{y_i^2})] L(θ)=−N1i∑N[log(pyi11)+log(pyi22)]
其中, y i 1 y_i^1 yi1, y i 2 y_i^2 yi2分别维第i个样本的实际起止位置。
参考文献
【论文笔记】QANet模型
QANet论文
DCN
Tensorflow实现:https://github.com/NLPLearn/QANet
Pytorch实现:https://github.com/hengruo/QANet-pytorch