各种插值
对于图像缩放上下采样问题,一般是先计算目标图(dst)每个像素点在源图(src)中对应的线性位置,计算公式:
s r c x = d s t x × ( s r c w d s t w ) src_x=dst_x \times (\displaystyle\frac{src_{w}}{dst_{w}}) srcx=dstx×(dstwsrcw)
s r c y = d s t y × ( s r c h d s t h ) src_y=dst_y \times (\displaystyle\frac{src_{h}}{dst_{h}}) srcy=dsty×(dsthsrch)
然后根据位置在源图中取值,但是一般计算下来对应回源图都是分数 ( s r c x , s r c y ) (src_x,src_y) (srcx,srcy),而对这个分数值的位置进行像素赋予有不同的方法规则,也就是不同的插值实现。
最邻近插值
线性插值
双线性插值
双三次插值
兰索思插值
更新中…
最邻近插值
对 ( s r c x , s r c y ) (src_x,src_y) (srcx,srcy)进行四舍五入,然后直接取对应源图上的像素点。即选择最近的像素进行插值,但是放大后的图像有很严重的马赛克,缩小后的图像有很严重的失真。
线性插值
简单理解就是线性问题。已知(x1, y1) 与 (x2, y2),计算 [x1, x2] 区间内某一位置 x 在直线上的y值。线性插值是以距离为权重的一种插值方式。
y − y 1 x − x 1 = y 2 − y 1 x 2 − x 1 \displaystyle\frac{y-y_1}{x-x_1}=\displaystyle\frac{y_2-y_1}{x_2-x_1} x−x1y−y1=x2−x1y2−y1
y = x 2 − x x 2 − x 1 y 1 + x − x 1 x 2 − x 1 y 2 y=\displaystyle\frac{x_2-x}{x_2-x_1}y_1+\displaystyle\frac{x-x_1}{x_2-x_1}y_2 y=x2−x1x2−xy1+x2−x1x−x1y2
双线性插值
双线性插值是在两个方向分别进行一次线性插值,利用了源图中 ( s r c x , s r c y ) (src_x,src_y) (srcx,srcy)点四周的四个真实存在的像素值来共同决定 ( s r c x , s r c y ) (src_x,src_y) (srcx,srcy)点位置的像素值
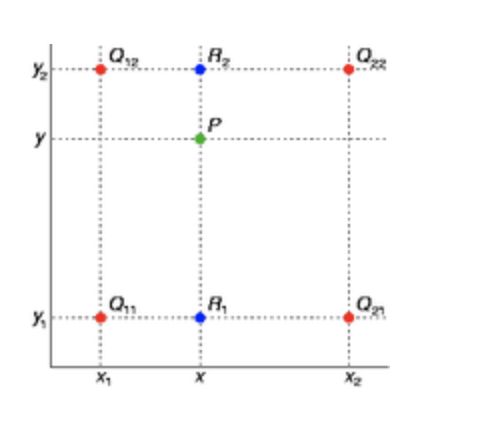
首先在x方向进行线性插值:
f ( x , y 1 ) ≈ x 2 − x x 2 − x 1 f ( Q 11 ) + x − x 1 x 2 − x 1 f ( Q 21 ) f(x,y_1)\approx \displaystyle\frac{x_2-x}{x_2-x_1}f(Q_{11})+\displaystyle\frac{x-x_1}{x_2-x_1}f(Q_{21}) f(x,y1)≈x2−x1x2−xf(Q11)+x2−x1x−x1f(Q21)
f ( x , y 2 ) ≈ x 2 − x x 2 − x 1 f ( Q 12 ) + x − x 1 x 2 − x 1 f ( Q 22 ) f(x,y_2)\approx \displaystyle\frac{x_2-x}{x_2-x_1}f(Q_{12})+\displaystyle\frac{x-x_1}{x_2-x_1}f(Q_{22}) f(x,y2)≈x2−x1x2−xf(Q12)+x2−x1x−x1f(Q22)
然后在 y 方向进行线性插值:
f ( x , y ) ≈ y 2 − y y 2 − y 1 f ( x , y 1 ) + y − y 1 y 2 − y 1 f ( x , y 2 ) f(x,y)\approx\displaystyle\frac{y_2-y}{y_2-y_1}f(x,y_1)+\displaystyle\frac{y-y_1}{y_2-y_1}f(x,y_2) f(x,y)≈y2−y1y2−yf(x,y1)+y2−y1y−y1f(x,y2)
合起来结果就是:
f ( x , y ) ≈ ( y 2 − y ) ( x 2 − x ) ( y 2 − y 1 ) ( x 2 − x 1 ) f ( Q 11 ) + ( y 2 − y ) ( x − x 1 ) ( y 2 − y 1 ) ( x 2 − x 1 ) f ( Q 21 ) + ( y − y 1 ) ( x 2 − x ) ( y 2 − y 1 ) ( x 2 − x 1 ) f ( Q 12 + ( y − y 1 ) ( x − x 1 ) ( y 2 − y 1 ) ( x 2 − x 1 ) f ( Q 22 ) f(x,y)\approx\displaystyle\frac{(y_2-y)(x_2-x)}{(y_2-y_1)(x_2-x_1)}f(Q_{11})+\displaystyle\frac{(y_2-y)(x-x_1)}{(y_2-y_1)(x_2-x_1)}f(Q_{21})+\displaystyle\frac{(y-y_1)(x_2-x)}{(y_2-y_1)(x_2-x_1)}f(Q_{12}+\displaystyle\frac{(y-y_1)(x-x_1)}{(y_2-y_1)(x_2-x_1)}f(Q_{22}) f(x,y)≈(y2−y1)(x2−x1)(y2−y)(x2−x)f(Q11)+(y2−y1)(x2−x1)(y2−y)(x−x1)f(Q21)+(y2−y1)(x2−x1)(y−y1)(x2−x)f(Q12+(y2−y1)(x2−x1)(y−y1)(x−x1)f(Q22)
双线性插值采用相邻的4个点,因此上述公式的分母都是1
双三次插值
上面的双线性插值是利用源图相邻的4个点,而双三次插值是利用最近的16个点(4x4)进行插值。
双三次插值利用BiCubic基函数求出16个像素点的权重, ( s r c x , s r c y ) (src_x,src_y) (srcx,srcy)位置点像素的值就等于源图16个像素点的加权叠加。
总:
源图像和目标图像几何中心的对齐。
将浮点运算转换成整数运算