尺取-算法详解及例题
1. 先看一道例题:http://acm.nefu.edu.cn/problemShow.php?problem_id=1814
题目的意思是给你一个n和s,然后给出n个数,求这n个数中和大于等于s的最小连续序列。
看一下第一组数据:
10 15
5 1 3 5 10 7 4 9 2 8
首先在不考虑时间的情况下可以这么干:
for(l=1;l<=n;l++) //从左边第一个数开始,取区间下限l
{
for(r=l;l<=n;l++) //在区间下限右边取区间上限r
{
check(l,r); //判断区间[l,r]中数的和是否等于s,是就和最小长度比较。
if(check) minlen=min(minlen,r-l+1)
}
}可以看的出来时间复杂度为o(n^2),但这给我们提供了一定的思路。
再看尺取算法的代码:
#include
using namespace std;
const int N=1e5+5;
int main()
{
int i,t,l,r;
int n,s;
int sum,len;
int a[N];
scanf("%d",&t);
while(t--)
{
sum=0;
scanf("%d%d",&n,&s);
len=n+1;
for(i=1;i<=n;i++) scanf("%d",&a[i]);
for(l=1,r=1;r<=n;r++) //设定左右区间初始化为1
{
sum+=a[r]; //不断扩大右区间
if(sum=s) sum-=a[l++]; //然后缩减区间,即扩大左区间,把多余部分踢掉
//使区间最小
len=min(len,r-l+1); //得到区间[l,r],判断长度
} //往复
if(len==n+1) printf("%d\n",0);
else printf("%d\n",len);
}
}
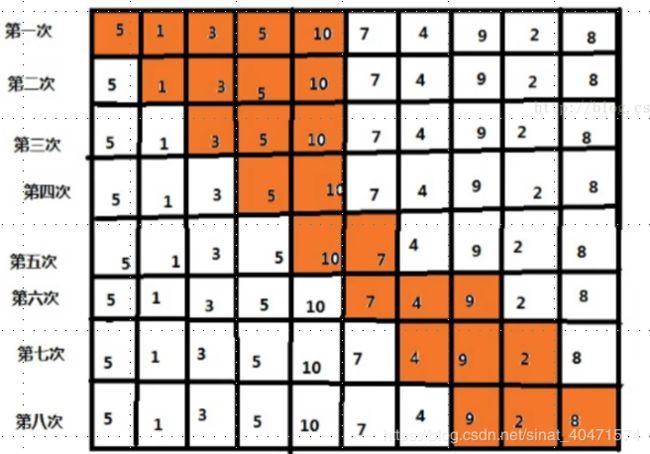
看下面这张表(黄色部分的和大于等于s):
为了更易于理解这种算法,看一种动物:尺蠖
这个算法的执行就好像它爬行的过程,先不停的把头往前探,然后收尾部,最后中间拱起来的部分就是一次爬行得到的区间,重复爬行动作不断向前。
对比着表看,就是从起点开始,不断伸长头部,直到和大等于s,然后收尾部,使和大等于s的情况下数的个数最少。得到一个区间,将区间长度和当前最小值比较并取最小值,然后继续往前爬行找下一个数。
看的出来这种算法的复杂度为o(n),因为l,r都只从1~n走了一次。
2. 再看第二道例题:http://acm.nefu.edu.cn/problemShow.php?problem_id=1813
概括起来就是给你一个只包含26个字母的字符串,求长度最小且包含26个字母的子串。
这题需要记录每个字母出现的次数,以及目前出现的字母数。
#include
using namespace std;
const int N=1e6+5; //这个要注意一下,题目的106意思是10^6,数组开太小会RE
int main()
{
int i,l,r;
int len,minlen,wordnum; //len-输入字符长度,minlen-所求最小长度,wordnum-当前找到字母数
int num[300]; //用于储存各字母出现个数,以ASCII码形式,ASCII最大127
char a[N]; //储存输入
scanf("%s",a);
len=strlen(a);
memset(num,0,sizeof(num));
minlen=N; //让最小值一开始很大
wordnum=0;
for(l=0,r=0;r1) //缩减区间,如果字母个数大于1说明后面已经有这个字母,可踢掉
{
num[a[l]]--;
l++; //踢掉多余的,其实还可以一步写成num[a[l++]]--;
}
minlen=min(minlen,r-l+1);
}
printf("%d\n",minlen);
} 3. 然后接下来就是稍微有点难度的题啦:
Language:http://acm.nefu.edu.cn/problemShow.php?problem_id=1845
题目的意思是找出包含所有数字的最小区间。
因为这题数据范围比较飘忽,用数组不太好,改用map,用集合set求数字个数。
#include
using namespace std;
const int N=1e6+5;
int pages[N];
mapidea;
setsetnum;
int main()
{
int l,r;
int p;
int ideanum,ideasum,minlen;
scanf("%d",&p);
ideasum=ideanum=0;
minlen=N;
idea.erase(idea.begin(),idea.end());
for(int i=1;i<=p;i++)
{
scanf("%d",&pages[i]);
setnum.insert(pages[i]);
}
ideanum=setnum.size();
setnum.clear();
for(l=1,r=1;r<=p;r++)
{
if(++idea[pages[r]]==1) ideasum++;
if(ideasum1) idea[pages[l++]]--;
minlen=min(minlen,r-l+1);
}
printf("%d\n",minlen);
} Sum of Consecutive Prime Numbers:http://acm.nefu.edu.cn/problemShow.php?problem_id=1816
题目的意思是给你一个数,求这个数能有多少种连续的素数构成。
首先得会素数筛,把素数表打出来。然后与之前不同的是这回不求最小长度,你要做的是让sum不断变大,直到大等于n,判断sum等不等于n,等于就确定了一种情况,大于就看看能不能削去尾巴,使sum变小,使sum等于n。
#include
using namespace std;
const int N=1e4+5;
int su[N],cnt;
bool isprime[N];
void prime()
{
cnt=1;
memset(isprime,1,sizeof(isprime));
isprime[0]=isprime[1]=0;
for(int i=2;i=n)
{
sum-=su[l++];
if(sum==n) num++;
}
}
printf("%d\n",num);
}
} Graveyard Design:http://acm.nefu.edu.cn/problemShow.php?problem_id=1817
题目的意思是给你一个数,判断它能有多少个连续的数的平方组成。
和上一题差不多,但有些细节要注意。
#include
using namespace std;
typedef long long LL;
LL grave[1000000][3];
int main()
{
int i,j;
LL square,sum,typenum,l,r;
scanf("%lld",&square);
sum=typenum=0;
int rmax=sqrt(square); //别忘了这一步,否则到1e14会超时
for(l=1,r=1;r<=rmax;r++)
{
sum+=r*r;
if(sum=square)
{
sum=sum-l*l;
l++;
if(sum==square)
{
grave[++typenum][0]=l;
grave[typenum][1]=r;
}
}
}
printf("%lld\n",typenum);
for(i=1;i<=typenum;i++)
{
printf("%lld ",grave[i][1]-grave[i][0]+1);
for(j=grave[i][0];j<=grave[i][1];j++)
printf("%lld ",j);
printf("\n");
}
}