如果题目版权限制,不能发表该题解,请私信,我会立刻删除博客。
注意:本题只允许使用C/C++或Java进行解答,其他编程语言提交均视作无效处理。
小W有一个电子时钟用于显示时间,显示的格式为HH:MM:SS,HH,MM,SS分别表示时,分,秒。其中时的范围为[‘00’,‘01’…‘23’],分的范围为[‘00’,‘01’…‘59’],秒的范围为[‘00’,‘01’…‘59’]。
但是有一天小W发现钟表似乎坏了,显示了一个不可能存在的时间“98:23:00”,小W希望改变最少的数字,使得电子时钟显示的时间为一个真实存在的时间,譬如“98:23:00”通过修改第一个’9’为’1’,即可成为一个真实存在的时间“18:23:00”。修改的方法可能有很多,小W想知道,在满足改变最少的数字的前提下,符合条件的字典序最小的时间是多少。其中字典序比较为用“HHMMSS”的6位字符串进行比较。
输入描述:
每个输入数据包含多个测试点。每个测试点后有一个空行。 第一行为测试点的个数T(T<=100)。 每个测试点包含1行,为一个字符串”HH:MM:SS”,表示钟表显示的时间。
输出描述:
对于每个测试点,输出一行。如果钟表显示的时间为真实存在的时间,则不做改动输出该时间,否则输出一个新的”HH:MM:SS”,表示修改最少的数字情况下,字典序最小的真实存在的时间。
【 网易互娱2018校招游戏研发工程师在线笔试 A】【水题】
#include
#include
#include
#include
#include
#include
#include
#include
题目描述
注意:本题只允许使用C/C++或Java进行解答,其他编程语言提交均视作无效处理。
字符迷阵是一种经典的智力游戏。玩家需要在给定的矩形的字符迷阵中寻找特定的单词。
在这题的规则中,单词是如下规定的:
1. 在字符迷阵中选取一个字符作为单词的开头;
2. 选取右方、下方、或右下45度方向作为单词的延伸方向;
3. 以开头的字符,以选定的延伸方向,把连续得到的若干字符拼接在一起,则
称为一个单词
。
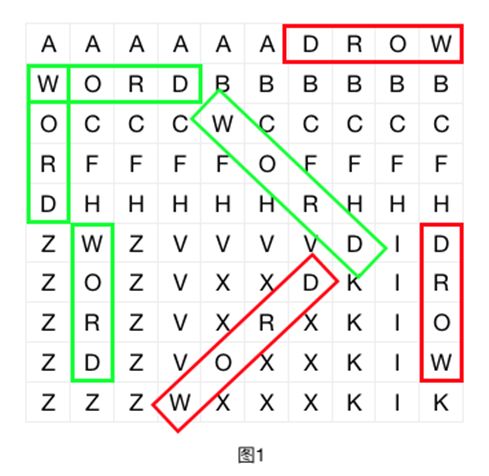
以图1为例,如果要在其中寻找单词"WORD",则绿色框所标示的都是合法的方案,而红色框所标示的都是不合法的方案。
现在的问题是,给出一个字符迷阵,及一个要寻找的单词,问能在字符迷阵中找到多少个该单词的合法方案。注意合法方案是可以重叠的,如图1所示的字符迷阵,其中单词"WORD"的合法方案有4种。
输入描述:
输入的第一行为一个正整数T,表示测试数据组数。 接下来有T组数据。每组数据的第一行包括两个整数m和n,表示字符迷阵的行数和列数。接下来有m行,每一行为一个长度为n的字符串,按顺序表示每一行之中的字符。再接下来还有一行包括一个字符串,表示要寻找的单词。 数据范围: 对于所有数据,都满足1<=T<=9,且输入的所有位于字符迷阵和单词中的字符都为大写字母。要寻找的单词最短为2个字符,最长为9个字符。字符迷阵和行列数,最小为1,最多为99。 对于其中50%的数据文件,字符迷阵的行列数更限制为最多为20。
输出描述:
对于每一组数据,输出一行,包含一个整数,为在给定的字符迷阵中找到给定的单词的合法方案数。
示例1
输入
3
10 10
AAAAAADROW
WORDBBBBBB
OCCCWCCCCC
RFFFFOFFFF
DHHHHHRHHH
ZWZVVVVDID
ZOZVXXDKIR
ZRZVXRXKIO
ZDZVOXXKIW
ZZZWXXXKIK
WORD
3 3
AAA
AAA
AAA
AA
5 8
WORDSWOR
ORDSWORD
RDSWORDS
DSWORDSW
SWORDSWO
SWORD
输出
【 网易互娱2018校招游戏研发工程师在线笔试 B】【水题】
#include
#include
#include
#include
#include
#include
#include
#include
题目描述
注意:本题只允许使用C/C++或Java进行解答,其他编程语言提交均视作无效处理。
小易的智能手机已经用了好多年了,手机里自带了一个流量统计的软件,记录了手机的流量信息。然而详细的流量信息只保留了最近一个月的情况,历史流量信息只保留了某些时刻的流量统计。
例如,其中一个流量记录条目为05/01/2017 18:00:00 10M,表示在2017年5月1日18点有10兆的流量记录。
小易从流量统计软件中导出了他过去的流量记录,现在他想知道他某一段时间内在流量统计软件中记录下来的总流量有多少。
输入描述:
每个输入数据仅包含一个测试点。 输入第一行首先给出流量记录的总条目数 N <= 100000。接下来N行,每行对应了一个流量记录。每条流量记录的格式为 月/日/年 时/分/秒 流量: MM/DD/YYYY hr:mi:se FLOWi 表示该时刻流量统计软件记录下了FLOWi (0 <= FLOWi <= 10000且为整数)兆的流量。 输入数据保证N条流量记录的时间是递增,且同一时间没有重复的流量记录。 接下来一行给出小易查询总流量的数目M <= 100000。接下来M行,每行表示第mj次查询的起始和结束时间点。格式如下: MM/DD/YYYY hr:mi:se MM/DD/YYYY hr:mi:se 输入数据保证每次查询的结束时间一定不会早于起始时间。所有的输入数据均合法。
输出描述:
输出结果包含M行,每行对应第mj次查询,每次查询的结果为包含起始和结束两个时刻的总流量。
示例1
输入
5
02/12/2016 00:00:00 10
02/18/2016 12:00:00 45
02/18/2016 23:59:59 8
02/19/2016 08:00:15 20
02/22/2016 13:00:00 31
4
01/01/2014 00:00:00 01/01/2017 00:00:00
11/11/2016 11:11:11 02/14/2017 00:05:20
02/12/2016 00:00:00 02/18/2016 23:00:00
02/18/2016 12:00:00 02/18/2016 12:00:00
输出
【 网易互娱2018校招游戏研发工程师在线笔试 C】【排序+前缀和】
#include
#include
#include
#include
#include
#include
#include
#include
题目描述
注意:本题只允许使用C/C++或Java进行解答,其他编程语言提交均视作无效处理。
在一局moba游戏中,你面对敌方的3个英雄,想完成一次三杀。敌方3名英雄都只剩普攻可以使用,而你有3个技能和一个普攻可用。
技能和普攻都有冷却时间,普攻的冷却时间都为1秒,而你的3个技能拥有相同的冷却时间cd秒。冷却时间为cd指的是:若你在第t1秒释放了该技能,那么在t1+cd秒才可以再次释放。所以普攻可以在每秒释放,但技能却不一定。你还有一个被动技能,每击杀一个敌人,则全部技能的冷却时间清零。
你是个执着的人,每次选择一个敌人后就不再更改目标直到打死这个敌人或自己死亡。
在每一秒的开始,如果你没有攻击目标(战斗开始时或上一秒刚击杀上一个目标),则选择一个攻击目标,否则继续锁定上一秒你的攻击目标。然后选择一个技能或普攻来攻击该目标,同时所有还活着的敌人也会攻击你。接下来所有人同时结算扣血,血量小于等于0的单位认为死亡。一个攻击力为atk的技能或普攻,会造成atk的血量损失。
已知3名敌人的当前血量和攻击力,以及你每一个技能的攻击力和普攻攻击力,问你是否可以完成这个漂亮的三杀。如果可以,那么完成三杀后你最多可以剩多少血量?(注意:同归于尽不算完成三杀)
输入描述:
输入的第一行是一个正整数T,表示样例数。 接下来是T个样例,每个样例的第一行是3个正整数hp, atk,cd,分别表示你的当前生命、普攻攻击力以及技能冷却时间。第二行是3个正整数x1, x2, x3,分别表示你的3个技能的攻击力。第三行是6个正整数hp1, y1, hp2, y2, hp3, y3,分别表示3个敌方英雄的血量和普攻攻击力。 对于30%的数据,所有血量不超过500,所有技能和普攻攻击力不超过50;对于100%的数据,所有血量不超过50000,所有技能和普攻攻击力不超过100。技能的冷却时间1 <= cd <= 10。
输出描述:
对于每一个样例,输出一个整数,表示完成三杀后你最多还剩多少血量。如果不能完成,输出-1。
示例1
输入
2
254 25 9
31 21 15
86 6 196 1 249 10
119 26 5
46 27 13
219 6 169 20 50 20
输出
备注:
样例1: 先攻击第一个敌人,使用1次技能1和3次普攻,共花费4秒击杀; 然后攻击第三个敌人,先使用1次技能1和8次普攻,此时使用一次技能1(刚好冷却结束)或普攻,共花费10秒; 最后攻击第二个敌人,先使用1次技能1,然后7次普攻,共花费8秒。 受到的总伤害为(6+1+10)*4 + (1 + 10) * 10 + 1 * 8 = 186,所以最终还剩68血量。 样例2: 无论怎样选择攻击策略,都无法完成三杀。
【 网易互娱2018校招游戏研发工程师在线笔试 D】【贪心+全排列】技能有CD,选择顺序和施法方案,最小伤害损失三杀
#include
#include
#include
#include
#include
#include
#include
#include
题目描述
注意:本题只允许使用C/C++或Java进行解答,其他编程语言提交均视作无效处理。
给定一个表达式,该表达式由以下规则生成:
1. "0"和"1"是合法表达式;
2. 如果x和y是合法表达式,那么"(x|y)"和"(x&y)"都是合法表达式
其中,|和&分别是与运算符和或运算符。
给定一个合法表达式,求该表达式最终的值。如果可以修改这个表达式的操作符:将|修改为&,将&修改为|,求最少需要修改多少个操作符可以修改表达式最终的值?
输入描述:
第一行是一个正整数T(T <= 20)。接下来T行,每一行是一个表达式。表达式不含空格,且输入保证该表达式是一个合法表达式。 对于30%的数据,表达式的长度不超过500; 对于100%的数据,表达式的长度不超过150000。
输出描述:
T行,每一行包含两个整数x, y,用空格隔开,分别表示表达式的值,以及最少需要修改多少个操作符可以修改表达式的值。如果无法通过修改操作符修改表达式的值,则y输出-1。
示例1
输入
3
((0|1)|(0|0))
((0|0)&(0|0))
(((1|0)|(0&0))|((1|0)|(0|1)))
输出
备注:
样例1:将表达式修改为((0&1)|(0|0))或((0|1)&(0|0)) 样例2:无论怎样修改,都无法将表达式结果变为1 样例3:有多个方案,其中一个为(((1&0)|(0&0))&((1|0)|(0|1))),但最少需要修改2个操作符
#include
#include
#include
#include
#include
#include
#include
#include