基于DTW相似度的Affinity Propagation(AP)聚类
基于DTW相似度的Affinity Propagation(AP)聚类
完整代码:https://github.com/SongDark/DTW_AP
数据
时序序列数据集 CharacterTrajectories,包含20种小写英文字母手写体的坐标序列。
| 训练集 | 测试集 | 类别数 | 序列长度 | 维度 | 数据类型 |
|---|---|---|---|---|---|
| 1422 | 1436 | 20 | 182 | 3 | Motion Gesture |
DTW距离
设有两个长度不相同的序列 x = [ x 1 , x 2 , ⋯ , x M ] x=[x_1,x_2,\cdots,x_M] x=[x1,x2,⋯,xM], y = [ y 1 , y 2 , ⋯ , y N ] y=[y_1,y_2,\cdots,y_N] y=[y1,y2,⋯,yN],DTW的计算步骤如下:
- 计算距离矩阵
D i j = ( x i − y j ) 2 D_{ij}=\sqrt{(x_i-y_j)^2} Dij=(xi−yj)2
- 计算累积距离矩阵
S i j = D i j + min ( S i , j − 1 , S i − 1 , j , S i − 1 , j − 1 ) S_{ij}=D_{ij}+\min (S_{i,j-1},S_{i-1,j},S_{i-1,j-1}) Sij=Dij+min(Si,j−1,Si−1,j,Si−1,j−1)
DTW的python实现
1. 普通实现
一般的dtw实现时间复杂度是 O ( T 2 ) O(T^2) O(T2),有个python的库fastdtw能达到近似线性 O ( T ) O(T) O(T),多样本之间的dtw距离矩阵计算如下:
import numpy as np
from fastdtw import fastdtw
l2_norm = lambda x, y: np.sqrt(np.sum(np.square(x-y)))
def np_dtw_matrix(dataset, lens, radius=20):
N = dataset.shape[0]
res = np.zeros((N, N))
for i in range(N):
for j in range(i+1, N):
res[i,j], _ = fastdtw(dataset[i][:lens[i], :], dataset[j][:lens[j], :], radius=20, dist=l2_norm)
res[j,i] = res[i,j]
return res
2. 并行实现
dtw的运算在样本维度上是互不依赖的,所以可以做并行。对于 N N N个样本,我们需要计算的距离矩阵大小为 N × N N \times N N×N,将其划分为 k × k k\times k k×k块,可以同时进行运算,将各子矩阵拼接起来即可。进一步地,由于距离矩阵是个对称阵,因此只需要计算上三角或下三角即可,即并行数为 k ( k + 1 ) / 2 k(k+1)/2 k(k+1)/2,在CPU核心数恒定的情况下,这个trick能够使 k k k 增大,从而节省时间。

3. Tensorflow实现
虽然fastdtw在众多dtw实现中已经很快了,但是当样本量很多的时候,还是比较慢。从样本维度上并行,可用GPU加速。
def tf_dtw_batch(X, Y, data_format='NWC'):
'''
X: [x1, x2, x3] (N,T,d) Y: [y1, y2, y3] (N,T,d)
returns the accumulated matrix D
D[len_x, len_y] is the DTW distance between x and y
'''
# X, Y : [N, T, d]
dist_mats = tf_l2norm_distmat_batch(X, Y, data_format=data_format) # [T*T, N]
batch_size, max_time = tf.shape(X)[0], tf.shape(X)[1]
d_array = tf.TensorArray(tf.float32, size=max_time*max_time, clear_after_read=False)
d_array = d_array.unstack(dist_mats) # read(t) returns an [N,] array at t timestep
D = tf.TensorArray(tf.float32, size=(max_time+1)*(max_time+1), clear_after_read=False)
# initalize
def cond_boder(idx, res):
return idx < max_time+1
def body_border_x(idx, res):
res = res.write(tf.to_int32(idx * (max_time+1)), 10000*tf.ones(shape=(batch_size, )))
return idx+1, res
def body_border_y(idx, res):
res = res.write(tf.to_int32(idx), 10000*tf.ones(shape=(batch_size, )))
return idx+1, res
_, D = tf.while_loop(cond_boder, body_border_x, (1, D))
_, D = tf.while_loop(cond_boder, body_border_y, (1, D))
def cond(idx, res):
return idx < (max_time+1) * (max_time+1)
def body(idx, res):
i = tf.to_int32(tf.divide(idx, max_time+1))
j = tf.mod(tf.to_int32(idx), max_time+1)
def f1():
dt = d_array.read(i*(max_time+1)+j-max_time-i-1)
min_v = tf.minimum(res.read((i - 1) * (max_time + 1) + j), res.read(i * (max_time + 1) + j - 1))
min_v = tf.minimum(min_v, res.read((i - 1) * (max_time + 1) + j - 1))
return res.write(idx, min_v + dt)
def f2():
return res
res = tf.cond(tf.less(i, 1) | tf.less(j, 1),
true_fn=f2,
false_fn=f1)
return idx+1, res
_, D = tf.while_loop(cond, body, (0, D))
D = D.stack()
D = tf.reshape(D, (max_time+1, max_time+1, batch_size)) # [T+1, T+1, N]
return D
时间消耗对比
1. 理论分析
计算耗时总是与样本数的平方成正比的,CPU并行与GPU版的区别在于,制约CPU并行运算上限是CPU核数,同时运算的子矩阵数不能超过CPU核数,而制约Tensorflow版运算上限的是显存,可以通过设置较大的 B a t c h _ S i z e Batch\_Size Batch_Size,同时算很多样本之间的距离,而且由于样本之间相互独立,所以每个Batch的运算时间实际上只与样本长度有关,当样本长度固定,每个Batch的运算时间也固定。
计算一对样本的DTW距离,设单核串行运算耗时 t 1 t_1 t1 秒,15核并行耗时 t 2 = t 1 / k t_2=t_1/k t2=t1/k ( k k k不一定能达到15),Tensorflow版跑一个大小为 B z Bz Bz 的Mini-Batch耗时 t 3 t_3 t3秒。现有 N N N 个样本,需要获得 N × N N\times N N×N 距离矩阵。三种方法的时间消耗理论上如下所示, T 1 T_1 T1、 T 2 T_2 T2 和 T 3 T_3 T3。可以预见,随着样本数增多,单核串行运算耗时呈指数增长,多核并行只能在前者的耗时上乘以一个小数,稍微打点折扣,而GPU版本在样本数不是很多时,只要不超显存,设置一个足够大的 B a t c h _ S i z e Batch\_Size Batch_Size 能有效减少所需 B a t c h Batch Batch 个数,从而大幅节省时间,而当样本数足够多时,耗时将与 B a t c h Batch Batch 个数呈正比,而 B a t c h Batch Batch 个数是与样本数的平方 N 2 N^2 N2 成正比的,因此样本数很多时,GPU版的耗时也将乘指数增长,但相比于CPU运算,仍有明显优势。
T 1 = t 1 × N ( N − 1 ) 2 T_1=t_1\times \frac{N(N-1)}{2} T1=t1×2N(N−1)
T 2 = t 1 k × N ( N − 1 ) 2 T_2=\frac{t_1}{k}\times \frac{N(N-1)}{2} T2=kt1×2N(N−1)
T 3 = t 3 × N ( N − 1 ) 2 B z = t 3 × B a t c h _ N u m T_3=t_3\times \frac{N(N-1)}{2Bz}=t_3 \times Batch\_Num T3=t3×2BzN(N−1)=t3×Batch_Num
2. 实测结果
以下是fastdtw和tensorflow版本DTW矩阵计算的时间消耗对比。tf_dtw根据样本量的不同需要设置不同的batch_size,过大的batch_size有使GPU显存不足的风险。
当样本数上升到1000,单核CPU运算已经至少要1天时间才能算完了,对整个CharacterTrajectory的2858样本进行运算,估计需要9天时间,15核并行运算可以缩减为21小时,而GPU版凭借较大的 B a t c h _ s i z e Batch\_size Batch_size (我设为10000),将时间缩减为1.8小时。
| N | N(N-1)/2 | fastdtw (r=10) | fastdtw_parallel (r=10, cpu=15) | tf_dtw (batches) |
|---|---|---|---|---|
| 10 | 45 | 8.07s | 1.29s | 16.31s (1) |
| 50 | 1,225 | 229.88 | 26.60 | 72.30 (5) |
| 100 | 4,950 | 959.57 | 102.74 | 72.97 (5) |
| 200 | 19,900 | ~4k (1.1h) | 402.69 | 77.13 (5) |
| 1,000 | 499,500 | ~100k (27h) | ~10k (2.8h) | 795.20 (50) |
| 2,858 | 4,082,653 | ~784k (9d) | ~78.4k (21h) | 6476.16 (400) |
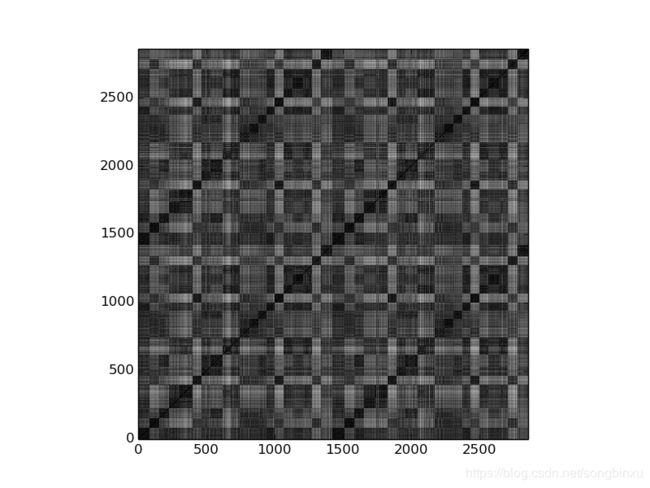
DTW距离矩阵
DTW矩阵上的值 D i j D_{ij} Dij 表示第 i i i 个样本和第 j j j 个样本之间的DTW距离,下图要从左下角往右上角看,横轴和纵轴都表示样本。图中颜色越黑表示距离越小,颜色越白表示距离越大。第1至1422个样本来自训练集,第1423至2858个样本来自测试集。
Affinity Propagation Clustering (AP聚类)
有关AP聚类的实现可参考这里。
现在我们得到了训练集样本两两之间的DTW矩阵,将这个距离矩阵的负值作为相似度矩阵(距离越大,负值越小,相似度越小),作为AP聚类的输入,获得若干个“中心”(centers),这样这个模型就训练完了。
测试阶段,从DTW距离矩阵上读出这些“中心”(centers)对应的行、测试样本对应的列,距离最小的center即为距离该测试样本最近的“中心”,将该中心的类别作为测试样本的预测类别,这样预测就完成了。
最终得到训练集的识别准确率为86.85%,测试集为83.43%。下图为测试集的混淆矩阵 C C C,纵轴表示标签,横轴表示预测类别, C i j C_{ij} Cij 表示标签为 i i i 的测试样本被模型识别为类别 j j j。
