单目slam LoopClosing之Sim3优化

sim3群运算

Sim3=(sR01×3t1)

最小表示： [ω,ν,σ] ， 其中 ω∈R3,ν∈R3,σ∈R ，分别表示旋转、位移、尺度增量。

---

逆运算：

S−1=⎛⎝1sRT01×3−1sRTt1⎞⎠

---

指数运算：

sim3=([w]×+σI3×301×3ν0)

expSim3(ν,ω,σ):=exp([w]×+σI3×301×3ν0)=(eσexp([ω]×)01×3Wν1)

W=(eσ−1σ)I+Aσ+(1−B)θθ(σ2+θ2)[w]×+(eσ−1σ−(B−1)σ+Aθσ2+θ2)[w]2×θ2

A=eσsin(θ) ， B=eσcos(θ) ， θ=∥ω∥2
则 s=eσ ， R=exp([ω]×) ， t=Wν

---

对数运算

log[sR01×3t1]=[log(R)+ln(s)I01×3W−1t0]

---

乘法运算：

(s1R101×3t11)∗(s2R201×3t21)=(s1s2R1R201×3s1R1t2+t11)

---

闭环纠正

由于我们slam系统一般都是增量式运动估计，所以随着系统的运行，误差不断的累计，譬如旋转误差和位移误差，而回环检测可以用来消除这种累计误差。
对于视觉slam我们常用基于视觉词典方法来检测回环，如DBow、FABMap等方法，本文着重介绍回环检测后的误差纠正，因此对于回环检测的方法不再细述。

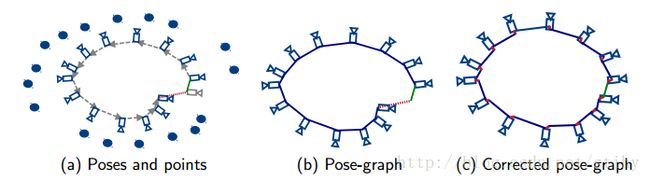
为了纠正累计误差，我们一般使误差大致均匀分布在整个相机Pose链上，从而当前帧和回环匹配帧误差不至于过大。如果我们优化所有的相机Pose和Point，一方面计算量过于庞大，另一方面由于要优化模型存在非凸性，因此可能做Full BA并不能达到我们我们期待收敛的结果。所以一般如图b只对相机的Pose作PoseGraph优化，然后再做个Pose和Point的Global Bundle Adjustment。
1. 6自由度的PoseGraph优化
假设对于相机两个Pose Tiw 和 Tjw ，两个Pose的相对变换 Tji=TjT−1i 。既然我们要优化两个相机的Pose Tiw 和 Tjw ，那么我们总要有测量量吧？而又不能优化特征所对应的MapPoint，所以就把初始两个相机的位姿相对变换作为测量值，这样优化前后整个相机Pose链帧间相对变换基本保持不变。
我们在 tangent space定义两个Pose误差为：

ei,j=log(Tji∗Tiw∗T−1jw)∨

Tiw∈{(Riw,tiw)|Riw∈SO3,tiw∈R3}

其中 log(.)∨:=(log(.))∨ ，先对SE3进行对数运算转换成se3，再vee-operator转装成 R6 矢量。则对整个PoseGraph作优化目标energy function：

χ2(T2,T3…Tm)=ΣTjieTi,jΩi,jei,j

其中 Ωij为信息矩阵 ，第一帧相机Pose固定，优化 T2,T3⋯Tm 。
2. 7自由度的PoseGraph优化
由于单目是纯相机投影模型。如下图所示，两个地图点距离相机5m、6m，相机运动2m，和两个地图点距离相机10m、12m，相机运动4m，所观察到的图像平面投影点坐标变换情况一样的。所以单目slam所构建地图与所估计的运动均up to sclae。

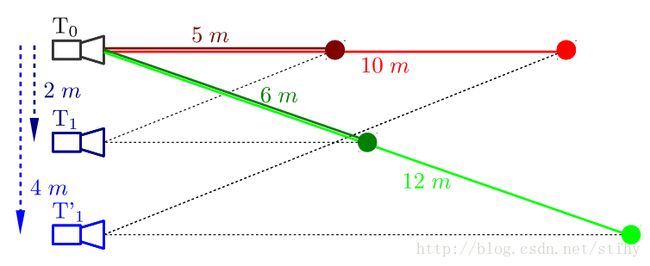
相机运动带来不只包括旋转误差、位移误差，还伴随带来尺度飘逸，比较明显现象如上图随着相机的运动，相机的轨迹越来越小，尺度也在不断的改变。如果我们像上述方法在SE3上作6自由度优化，虽然可以纠正旋转和位移飘逸，却不能处理scale drift。
定义在sim3上误差：

ei,j=log(Sji∗Siw∗S−1jw)∨sim3

和上述6自由度优化类似，我们定义优化初始估计值和测量值：

Siw=(Riw,tiw,s=1)，其中(Riw,tiw)=Tiw

Sji=(Rji,tji,s=1)，其中(Rji,tji)=Tji

其中对于回环帧 sloop≠1 ，我们不能像其他帧一样假设s=1，否则所有帧尺度都为1，没有尺度误差怎么优化尺度呢。一般对于检测到回环匹配两帧，我们都会采用附录【1】方法计算两帧间Sim3。
假设优化后Pose的Sim3为 Scorjw=(Rjw,tjw,s) ，则纠正之后Pose：

Tcorjw=(Rjw,1stjw)

Point的3D坐标 Pkw 纠正为：

wPcork=ScorwjTjwwPk

---

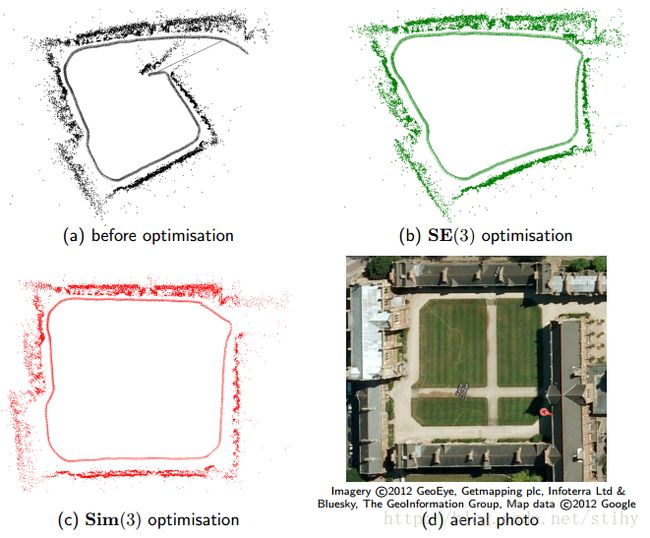
对比6自由度优化和7自由度优化，会发现在7自由Sim3上优化后结果更加接近于真实值。

附录：
[1]Closed-form solutionof absolute orientation using unit quaternions.
[2]Scale Drift-Aware Large Scale Monocular SLAM.