K-均值聚类（Python3）学习笔记

K-均值聚类（Python3）

1. K均值算法

• K-均值是发现给定数据集的$k$个簇的算法。簇个数$k$是由用户给定的，每个簇通过其质心（centroid），即簇中所有点的中心来描述。

• 给定样本集$D=\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_m\}$，“$k$均值”（$k$-means）算法所得簇划分$C=\{C_1,C_2,\cdots ,C_k\}$最小化平方误差$$E=\sum _{i=1}^k\sum _{\mathbf{x}\in C_i}\Vert \mathbf{x}-{\mathbf{\mu }}_i{\Vert }_2^2$$
  其中${\mathbf{\mu }}_i=\frac{1}{|C_i|}{\Sigma }_{\mathbf{x}\in C_i}\mathbf{x}$是簇$C_i$的均值向量。直观来看，上式在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度，$E$值越小则簇内样本相似度越高。

• 工作流程:
  创建k个点作为起始质心（经常是随机选择）
  当任意一个点的簇分配结果发生改变时
    对数据集中的每个数据点
      对每个质心
        计算质心与数据点的距离
      将数据点分配到距其最近的簇
    对每一个簇，计算簇中所有点的均值并将均值作为质心

• 优点：容易实现。

• 缺点：可能收敛到局部最小值，在大规模数据集上收敛较慢。

• 适用数据类型：数值型数据。

1.1 K-均值聚类支持函数Python3实现

from numpy import *
import matplotlib
import matplotlib.pyplot as plt

#导入数据集
def loadDataSet(filename):
    dataMat = []
    fr = open(filename)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float, curLine))
        dataMat.append(fltLine)
    return dataMat
#计算两个向量的欧式距离
def distEclud(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2)))

#生成随机质心
def randCent(dataSet, k):
    n = shape(dataSet)[1]
    centroids = mat(zeros((k, n)))
    for j in range(n):
        minJ = min(dataSet[:, j])
        rangeJ = float(max(dataSet[:, j]) - minJ)
        centroids[:, j] = minJ + rangeJ * random.rand(k,1)
    return centroids

#K-均值聚类算法
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m, 2)))#簇分配结果矩阵，存储簇索引值与误差
    centroids = randCent(dataSet, k)
    clusterChanged = True
    while clusterChanged:#迭代标志
        clusterChanged = False
        for i in range(m):
            minDist = inf
            minIndex = -1
            for j in range(k):#寻找最近质心
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI
                    minIndex = j
            if clusterAssment[i,0] != minIndex:#如果簇分配结果发生变化，更新迭代标志
                clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2#重新分配簇结果
        print (centroids)
        for cent in range(k):
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#获取给定簇的所有点
            centroids[cent,:] = mean(ptsInClust, axis=0)#沿矩阵的列方向计算它们的均值
    return centroids, clusterAssment

def plotCentroids(datMat, centroids, clusterAssment, k):
    fig = plt.figure()
    ax  = fig.add_subplot(111)
    for i in range(k):
        ax.scatter(datMat[[nonzero(clusterAssment[:,0] == float(i))[0]],0].flatten().A[0], datMat[[nonzero(clusterAssment[:,0] == float(i))[0]],1].flatten().A[0], marker="^", s=90)
    ax.scatter(centroids[:,0].flatten().A[0], centroids[:,1].flatten().A[0], marker="+", s=300, c="black")

datMat = mat(loadDataSet('testSet.txt'))
myCentroids, clustAssing = kMeans(datMat,4)

[[ 2.05223983 -3.0746459 ]
 [ 2.07512432  3.50918187]
 [-2.18388394 -1.47117211]
 [ 0.27725078  5.1426455 ]]
[[ 2.65077367 -2.79019029]
 [ 2.66534547  2.99911595]
 [-3.4859745  -2.31300105]
 [-2.10585717  3.15782844]]
[[ 2.65077367 -2.79019029]
 [ 2.6265299   3.10868015]
 [-3.53973889 -2.89384326]
 [-2.46154315  2.78737555]]

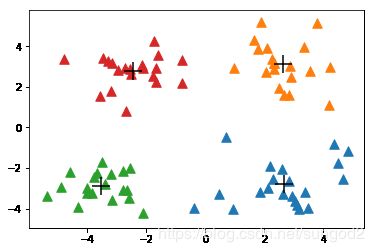
plotCentroids(datMat, myCentroids, clustAssing, 4)

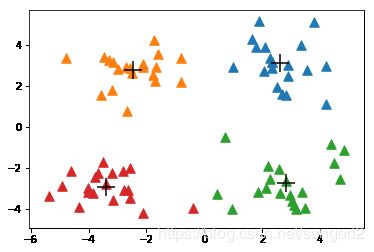
• 上面的结果给出了四个质心。可以看到，经过几次迭代后K-均值算法收敛。到目前为止，关于聚类的一切进展都很顺利，但事实并不总是如此。接下来会讨论K-均值算法可能出现的问题及其解决办法。

1.2 使用后处理来提高聚类性能

• 前面提到的，在K-均值聚类中簇的数目k是一个用户预先定义的参数，那么用户怎么才能知道k的选择是否正确？如何才能知道生成的簇比较好呢？在包含簇分配结果的矩阵中保存着每个点的误差，即该点到簇质心的距离平方值。下面会讨论利用该误差来评价聚类质量的方法。

• 假如我们将k的值设为3，那么它的运行结果如下图所示。可以看出，点的簇分配结果值没有那么准确。K-均值算法收敛但聚类效果差的原因是，K-均值算法收敛到了局部最小值，而不是全局最小值。

• 一种用于度量聚类效果的指标是SSE(Sum of Squared Error，误差平方和），对应clusterAssment矩阵的第一列之和。SSE值越小表示数据点越接近它们的质心，聚类效果也越好。因为对误差取了平方，因此更重视那些远离中心的点。

• 一种肯定可以降低SSE值得方法是增加簇的个数，但这违背了聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。

• 如何进行改进：可以对生成的簇进行后处理，一种方法是将具有最大的SSE值得簇划分为两个簇。具体实现时可以将最大簇包含得点过滤出来并在这些点上运行K-均值算法。

• 为了保持簇总数不变，可以将某两个簇进行合并。

• 有两种可以量化得方法：合并最近的质心，或者合并两个使得SSE增幅最小的质心。第一种思路通过计算所有质心之间的距离，然后合并距离最近的两个点来实现。第二种方法需要合并两个簇然后计算总SSE值。必须在所有可能的两个簇上重复上述处理过程，直到找到合并最佳的两个簇为止。

datMat = mat(loadDataSet('testSet.txt'))
myCentroids, clustAssing = kMeans(datMat,4)
plotCentroids(datMat, myCentroids, clustAssing, 4)

[[ 1.96818879  3.10418929]
 [-2.66894365  2.35308276]
 [ 3.56299862  0.14036498]
 [-4.42485328 -4.1647096 ]]
[[ 2.52792822  3.30405044]
 [-2.46154315  2.78737555]
 [ 2.8675685  -2.36043623]
 [-3.38237045 -2.9473363 ]]
[[ 2.6265299   3.10868015]
 [-2.46154315  2.78737555]
 [ 2.80293085 -2.7315146 ]
 [-3.38237045 -2.9473363 ]]

1.3 二分K-均值算法

• 为克服K-均值算法收敛于局部最小值的问题，有人提出了另一个称为二分K-均值（bisecting K-meams）的算法。该算法首先将所有点作为一个簇，然后将该簇一分为二。之后选择一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。

• 伪代码：
  将所有点看成一个簇
  当簇数目小于k时
    对于每一个簇
      计算总误差
      在给定的簇上面进行K-均值聚类（k=2）
      计算将该簇一分为二之后的总误差
    选择使得误差最小的那个簇进行划分操作

• 另一种做法是选择SSE最大的簇进行划分，直到簇数目达到用户指定的数目为止。

#二分K-均值聚类算法
def biKmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))#存储簇分配结果及平方误差
    centroid0 = mean(dataSet, axis=0).tolist()[0]#计算整个数据集的质心
    centList = [centroid0[0]]#使用一个列表保留所有质心
    for j in range(m):
        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2#计算每个点到质心的误差值
    while(len(centList) < k):#该循环不停对簇进行划分，直到得到想要的簇的数目
        lowestSSE = inf #将SSE值设为无穷大
        for i in range(len(centList)):  #遍历簇列表中的所有簇
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A == i)[0],:]#将该簇中的所有点看成一个小的数据集。
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)#生成两个质心同时给出每个簇的误差值
            sseSplit = sum(splitClustAss[:,1]) 
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A != i)[0],1])
            print("sseSplit, and NotSplit: ", sseSplit, sseNotSplit)
            if(sseSplit + sseNotSplit) < lowestSSE:  #如果该划分的SSE值最小，则本次划分被保存 
                bestCentToSplit = i
                bestNewCents = centroidMat
                bestClustAss = splitClustAss.copy()
                lowestSSE = sseSplit + sseNotSplit
        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0], 0] = len(centList)#更新簇的分配结果
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0], 0] = bestCentToSplit
        print("the bestCentToSplit is: ",bestCentToSplit)
        print("the len of bestClustAss is: ",len(bestClustAss))
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]
        centList.append(bestNewCents[1,:].tolist()[0])
        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0], :] = bestClustAss
    return mat(centList), clusterAssment

datMat3 = mat(loadDataSet('testSet2.txt'))

centList, myNewAssments = biKmeans(datMat3, 3)
centList

[[ 3.37991172  3.38570226]
 [-3.10486239 -2.37443875]]
[[ 1.86138027  3.22269712]
 [-1.70174271 -0.30206818]]
[[ 2.35797261  3.21160974]
 [-1.72153338 -0.00938424]]
[[ 2.76275171  3.12704005]
 [-1.73028592  0.20133246]]
[[ 2.93386365  3.12782785]
 [-1.70351595  0.27408125]]
sseSplit, and NotSplit:  541.2976292649145 0.0
the bestCentToSplit is:  0
the len of bestClustAss is:  60
[[3.38922822 0.8721925 ]
 [3.91147439 0.73983691]]
[[2.75314728 3.06695644]
 [4.560311   3.6756705 ]]
[[2.48449707 2.95091147]
 [4.2819634  3.658577  ]]
sseSplit, and NotSplit:  25.535514707587865 501.7683305828214
[[-2.71396475  1.10408322]
 [-1.82642235 -3.1436269 ]]
[[-2.94737575  3.3263781 ]
 [-0.45965615 -2.7782156 ]]
sseSplit, and NotSplit:  67.2202000797829 39.52929868209309
the bestCentToSplit is:  1
the len of bestClustAss is:  40





matrix([[ 2.93386365,  3.12782785],
        [-2.94737575,  3.3263781 ],
        [-0.45965615, -2.7782156 ]])

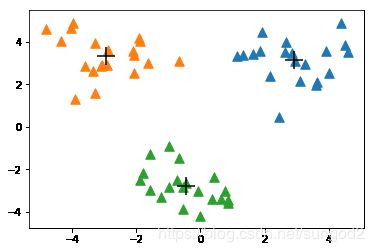
plotCentroids(datMat3, centList, myNewAssments, 3)

• 上述函数会运行多次，聚类会收敛到全局最小值，而原始的kMeans()函数偶尔会陷入局部最小值。

本章小结

• 聚类是一种无监督的学习方法。聚类区别于分类，即事先不知道要寻找的内容，没有预先设定好的目标变量。
• 聚类将数据点归到多个簇中，其中相似的数据点归为同一簇，而不相似的点归为不同的簇。相似度的计算方法有很多，具体的应用选择合适的相似度计算方法。
• K-means聚类算法，是一种广泛使用的聚类算法，其中k是需要指定的参数，即需要创建的簇的数目，K-means算法中的k个簇的质心可以通过随机的方式获得，但是这些点需要位于数据范围内。在算法中，计算每个点到质心得距离，选择距离最小的质心对应的簇作为该数据点的划分，然后再基于该分配过程后更新簇的质心。重复上述过程，直至各个簇的质心不再变化为止。
• K-means算法虽然有效，但是容易受到初始簇质心的情况而影响，有可能陷入局部最优解。为了解决这个问题，可以使用另外一种称为二分K-means的聚类算法。二分K-means算法首先将所有数据点分为一个簇；然后使用K-means（k=2）对其进行划分；下一次迭代时，选择使得SSE下降程度最大的簇进行划分；重复该过程，直至簇的个数达到指定的数目为止。实验表明，二分K-means算法的聚类效果要好于普通的K-means聚类算法。