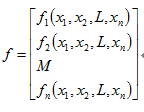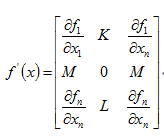C语言牛顿迭代法求解非线性方程组
牛顿法
牛顿法是一种线性化方法,其基本思想是将非线性方程f(x)=0逐步归结为某种线性方程来求解。
设已知方程有近似根(假定),将函数在点展开,有
于是方程可近似地表示为
这是个线性方程,记其根为,则的计算公式
这就是牛顿法。
一、算法及流程
对于非线性方程
在处按照多元函数的泰勒展开,并取线性项得到
其中
这样便得到迭代公式:
这边是牛顿迭代法的算法过程,牛顿迭代法是工程上应用最多的一种非线性方程组的计算方程法。
二、代码及实现
/*
*功能:牛顿迭代法求解非线性方程
*姓名:孙泽 日期:2019年4月24日
*/
#include
#include
#define tol -10 /*精度*/
/*--------------------
*方程组及一阶导数
--------------------*/
double func1(double x, double y){
return x*x-2*x-y+0.5;
}
double func2(double x, double y){
return x*x+4*y*y-4;
}
double func11(double x, double y){
return 2*x-3;
}
double func21(double x, double y){
return 2*x+8*y;
}
int main(void){
unsigned int c_times = 0;
double r_x,r_y,p_x,p_y;
double n_tol=1;
p_x = -1;
p_y = 1;
n_tol = pow((double)10,tol); /*误差界限*/
printf("%s\t%s\t%s\n","迭代次数","X","Y");
/*牛顿迭代*/
for(c_times = 1; c_times < 1000; c_times++){
r_x = p_x - func1(p_x,p_y)/func11(p_x,p_y);
r_y = p_y - func2(p_x,p_y)/func21(p_x,p_y);
printf("%d\t%-.20lg\t%-.20lg\n",c_times,r_x,r_y);
if(((p_x-r_x)>0?p_x-r_x:r_x-p_x) < n_tol)
break;
p_x = r_x;
p_y = r_y;
}
printf("迭代次数:%d\n",c_times-1);
printf("方程组解:\n");
printf("%.20lg\t%.20lg\n",r_x,r_y);
getchar();
return 0;
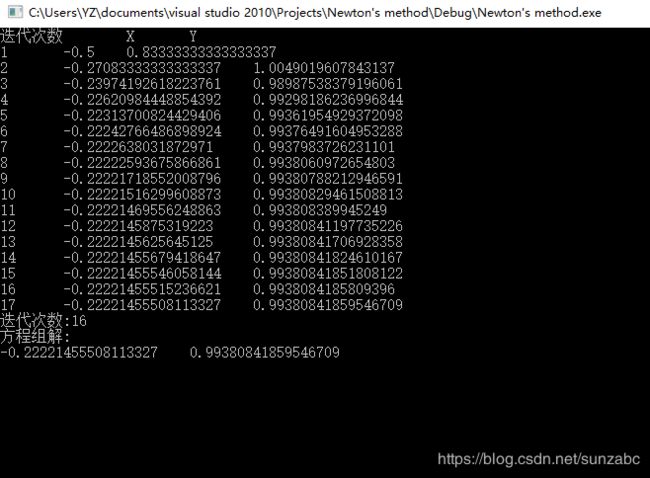
} 三、运算结果