叶丙成-概率-chapter4-随机变量-累积分布函数CDF-概率质量函数PMF-伯努利分布-二项分布-均匀分布
国立台湾大学叶丙成《机率》课程学习-chapter4-随机变量-累积分布函数CDF-概率质量函数PMF-伯努利分布-二项分布-均匀分布
- 4.1 随机变量
- 4.1.1 随机变量(random variable,R.V.)定义
- 4.1.2 随机变量的本质
- 4.1.3 随机变量的种类
- 4.1.4 随机变量的函数
- 4.2 累积分布函数(cumulative distribution function,CDF)
- 4.2.1 何谓CDF?
- 4.2.2 CDF用处?
- 4.2.3 CDF的性质
- 4.3 概率质量函数(probability mass function,PMF)(离散随机变量特有)
- 4.3.1 什么是PMF
- 4.3.2 PMF与CDF的关系(离散随机变量通常只使用整数)
- 4.4 离散概率分布(discrete probability distributions)
- 4.4.1 Bernoulli概率分布(伯努利分布)
- 4.4.2 Binomial概率分布(二项分布)
- 4.4.3 Uniform概率分布(均匀分布)
- 4.4.4 学这些概率分布有什么用
视频地址1(需科学上网,有需要可以留言要云分享)
视频地址2-B站
4.1 随机变量
4.1.1 随机变量(random variable,R.V.)定义
随机变量(random variable,R.V.)定义:是一个用来把实验结果(outcome)数字化的表示方式。
存在的意义:可以让概率的推导更数学,更简明
注:随机变数通常使用大写英文字母表示
4.1.2 随机变量的本质
随机变量的本质?函数!
随机变量其实是一个函数,给 X X X一个outcome,就返回一个对应的数字。数学上的表示法: X : S → ℜ X:S\to \Re X:S→ℜ(映射)
4.1.3 随机变量的种类
- 离散随机变量(Discrete R.V.)
EX1:店员的微笑: X ( 笑 ) = 1 , X ( 不 笑 ) = 0 ⇒ X = 0 , X = 1 X(笑)=1,X(不笑)=0\Rightarrow X=0,X=1 X(笑)=1,X(不笑)=0⇒X=0,X=1
EX2:小美的三个司机: X ( 明 ) = 0 , X ( 华 ) = 1 , X ( 圆 ) = 2 ⇒ X = 0 , X = 1 , X = 2 X(明)=0,X(华)=1,X(圆)=2\Rightarrow X=0,X=1,X=2 X(明)=0,X(华)=1,X(圆)=2⇒X=0,X=1,X=2
EX3:小明告白多少次才能成功: X ( 0 次 ) = 0 , X ( 1 次 ) = 1 , X ( 2 次 ) = 2 , ⋯ ⇒ X = 0 , X = 1 , X = 2 , … X(0次)=0,X(1次)=1,X(2次)=2,\dots\Rightarrow X=0,X=1,X=2,\dots X(0次)=0,X(1次)=1,X(2次)=2,⋯⇒X=0,X=1,X=2,…
注:离散随机变量并不代表只有有限多个case(可以是可数无穷多个)。 - 连续随机变量(continuous R.V)
EX1:幸运之轮: X X X可以说 [ 0 , 1 ] [0,1] [0,1]之间的任意数字
注:连续随机变量的值是有无穷多个,而且是不可数的无穷多个。 - 什么是可数的,什么是不可数的?
- 可数的:一个集合如果是可数的,这代表它包含的东西是可以一个个被数的,不管用什么方法数它里面的东西,它里面的任意一个东西,总是会被数到的。
EX:正偶数集合 { 2 , 4 , 6 , 8 , 10 , … } \{2, 4, 6, 8,10,\dots \} {2,4,6,8,10,…}是可数的,从中随意取一个数字,总是可以数到的。 - 不可数的:一个集合如果是不可数的,这代表它包含的东西是无法可以一个个被数的,不管用什么方法数它里面的东西,它里面一定有一样东西是你没数到的!
EX:0到1之间的所有数字的集合是不可数的! - 扩展-无穷多的世界:
- EX1:正整数的集合和正偶数的集合相比,哪个集合里面的东西比较多?答案是一样多,正整数的集合中的值乘2即可和正偶数集合产生一一对应关系。
- EX1:“长度为1的线段上的点”与“边长为1的正方形平面上的点”,这两个集合,哪一个点的数量比较多?答案是一样多。
- 注:在无穷多的世界里面,评价两个集合相等,不能使用“你中有我,我中有你”。而是使用是否可以找到一个方法(映射),使两个无穷集合可以找到一个一一对应关系,如果有,两无穷集合是相等的。
- 可数的:一个集合如果是可数的,这代表它包含的东西是可以一个个被数的,不管用什么方法数它里面的东西,它里面的任意一个东西,总是会被数到的。
4.1.4 随机变量的函数
阿宅若看到店员微笑,就会点200的套餐。如果店员不笑,他就点15的饮料。请问阿宅的消费金额 W W W是随机变量嘛?
解:店员表情可以由随机变量 X X X代表: X ( 微 笑 ) = 0 , X ( 不 笑 ) = 15 X(微笑)=0,X(不笑)=15 X(微笑)=0,X(不笑)=15
W W W是 X X X的函数: W ( X ( 微 笑 ) ) = 200 , W ( X ( 不 笑 ) ) = 15 W(X(微笑))=200,W(X(不笑))=15 W(X(微笑))=200,W(X(不笑))=15
所以 W W W也是喂outcome吐数字!因此, W W W也是一个随机变量!
注:随机变量的函数,也是个随机变量
4.2 累积分布函数(cumulative distribution function,CDF)
4.2.1 何谓CDF?
对任一个随机变量 X X X,我们定义其 C D F CDF CDF为
F X ( x ) = def P ( X ≤ x ) F_X(x) \overset{\text{def}}{=} P(X \leq x) FX(x)=defP(X≤x)
注:含等号
EX:幸运之轮
F X ( 0.5 ) = P ( x ≤ 0.5 ) = 1 2 F_X(0.5)=P(x\le 0.5)=\frac{1}{2} FX(0.5)=P(x≤0.5)=21
4.2.2 CDF用处?
- 最有用的用途
计算 X X X落在某范围内的概率
EX1:如图计算 P ( 3 < X ≤ 5 ) P(3<X\le5) P(3<X≤5)的概率

可以将其转化为两个 C D F CDF CDF相减,
P ( 3 < X ≤ 5 ) = P ( X ≤ 5 ) − P ( X ≤ 3 ) P(3<X\le5)=P(X\le5)-P(X\le3) P(3<X≤5)=P(X≤5)−P(X≤3)
EX2:对比 P ( 3 < X ≤ 5 ) P(3<X\le5) P(3<X≤5)与 P ( 3 ≤ X ≤ 5 ) P(3\le X\le5) P(3≤X≤5)区别(差一个等号):
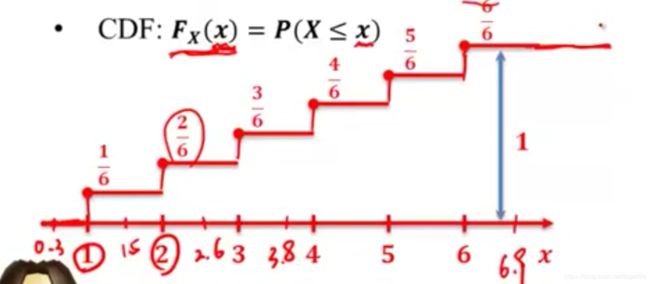
P ( 3 ≤ X ≤ 5 ) = P ( X ≤ 5 ) − P ( X ≤ 3 ) + P ( X = a ) P(3\le X\le5)=P(X\le5)-P(X\le3) + P(X=a) P(3≤X≤5)=P(X≤5)−P(X≤3)+P(X=a) - 离散随机变量的 C D F CDF CDF长什么样?(阶梯状)
EX: X X X为骰子的点数,故 P ( X = 1 ) = P ( X = 2 ) = P ( X = 3 ) = P ( X = 4 ) = P ( X = 5 ) = P ( X = 6 ) = 1 2 P(X=1)=P(X=2)=P(X=3)=P(X=4)=P(X=5)=P(X=6)=\frac{1}{2} P(X=1)=P(X=2)=P(X=3)=P(X=4)=P(X=5)=P(X=6)=21
解: C D F : F X ( x ) = P ( X ≤ x ) CDF:F_X(x)=P(X\le x) CDF:FX(x)=P(X≤x) - 连续随机变量的 C D F CDF CDF长什么样?
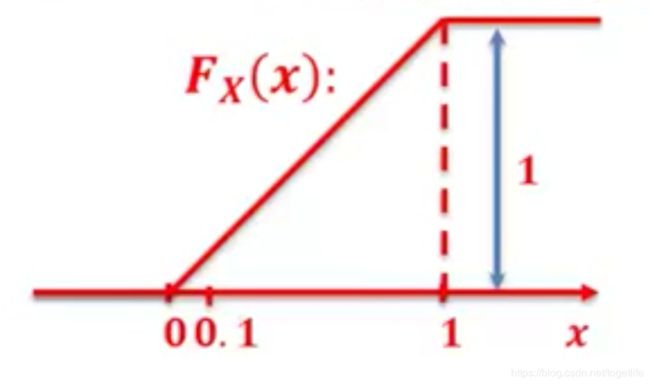
EX: X X X为幸运之轮所停下的数字, x ∈ [ 0 , 1 ) x \in [0,1) x∈[0,1),
解: C D F : F X ( x ) = P ( X ≤ x ) CDF:F_X(x)=P(X\le x) CDF:FX(x)=P(X≤x)- F X ( − 0.1 ) = P ( X ≤ − 0.1 ) = 0 F_X(-0.1)=P(X \le -0.1) = 0 FX(−0.1)=P(X≤−0.1)=0
- F X ( 0.1 ) = P ( 0 ≤ X ≤ 0.1 ) = 0.1 F_X(0.1)=P(0 \le X \le 0.1) = 0.1 FX(0.1)=P(0≤X≤0.1)=0.1
- F X ( 0.5 ) = P ( 0 ≤ X ≤ 0.5 ) = 0.5 F_X(0.5)=P(0 \le X \le 0.5) = 0.5 FX(0.5)=P(0≤X≤0.5)=0.5
- F X ( 1 ) = P ( 0 ≤ X ≤ 1 ) = 1 F_X(1)=P(0 \le X \le 1) = 1 FX(1)=P(0≤X≤1)=1
- F X ( 1.7 ) = P ( 0 ≤ X ≤ 1.7 ) = 1 F_X(1.7)=P(0 \le X \le 1.7) = 1 FX(1.7)=P(0≤X≤1.7)=1
- P ( 0.3 < x ≤ 0.5 ) = F X ( 0.5 ) − F X ( 0.3 ) = 0.5 − 0.3 = 0.2 P(0.3< x \le 0.5) = F_X(0.5)-F_X(0.3)=0.5-0.3=0.2 P(0.3<x≤0.5)=FX(0.5)−FX(0.3)=0.5−0.3=0.2
- P ( 0.3 < x < 0.5 ) = F X ( 0. 5 − ) − F X ( 0.3 ) = 0.5 − 0.3 = 0.2 P(0.3< x < 0.5) = F_X(0.5^-)-F_X(0.3)=0.5-0.3=0.2 P(0.3<x<0.5)=FX(0.5−)−FX(0.3)=0.5−0.3=0.2
- 注: 0. 5 − 0.5^- 0.5−表示无限接近 0.5 0.5 0.5的一个点
4.2.3 CDF的性质
- 离散随机变量之 C D F CDF CDF
F X ( x + ) = F X ( x ) F_X(x^+)=F_X(x) FX(x+)=FX(x)
F X ( x − ) = F X ( x ) − P ( X = x ) F_X(x^-)=F_X(x)-P(X=x) FX(x−)=FX(x)−P(X=x)
注1: x + x^+ x+表示比 x x x大一点,但无限接近 x x x的一个值(参考《数学分析》极限定义中的 ϵ \epsilon ϵ)
注2: x − x^- x−表示比 x x x小一点,但无限接近 x x x的一个值 - 连续随机变量之 C D F CDF CDF
F X ( x + ) = F X ( x ) = F X ( x − ) F_X(x^+)=F_X(x)=F_X(x^-) FX(x+)=FX(x)=FX(x−) - 共同性质
F X ( − ∞ ) = P ( x ≤ − ∞ ) = 0 F_X(-\infty)=P(x\le-\infty)=0 FX(−∞)=P(x≤−∞)=0
F X ( + ∞ ) = P ( x ≤ + ∞ ) = 1 F_X(+\infty)=P(x\le+\infty)=1 FX(+∞)=P(x≤+∞)=1
0 ≤ F X ( x ) ≤ 1 0 \le F_X(x)\le 1 0≤FX(x)≤1
4.3 概率质量函数(probability mass function,PMF)(离散随机变量特有)
4.3.1 什么是PMF
- 对任一个整数值的离散随机变量 X X X,我们定义其 P M F PMF PMF为函数:
p X ( x ) = def P ( X = x ) p_X(x) \overset{\text{def}}{=} P(X = x) pX(x)=defP(X=x) - EX: X X X为公平骰子之点数
p X ( 3 ) = P ( X = 3 ) = 1 6 p_X(3)=P(X=3)=\frac{1}{6} pX(3)=P(X=3)=61
4.3.2 PMF与CDF的关系(离散随机变量通常只使用整数)
- F X ( 2.5 ) = P ( X ≤ 2.5 ) = P ( X = 2 ) + P ( X = 1 ) + P ( X = 0 ) + P ( X = − 1 ) + ⋯ = ∑ n = − ∞ 2 = ∣ 2.5 ∣ P ( X = n ) F_X(2.5)=P(X\le2.5)=P(X=2)+P(X=1)+P(X=0)+P(X=-1)+\dots=\sum_{n=- \infty}^{2=|2.5|}P(X=n) FX(2.5)=P(X≤2.5)=P(X=2)+P(X=1)+P(X=0)+P(X=−1)+⋯=∑n=−∞2=∣2.5∣P(X=n)
- 对任何 x x x
F X ( x ) = ∑ n = − ∞ ∣ x ∣ P X ( n ) F_X(x)=\sum_{n=-\infty}^{|x|}P_X(n) FX(x)=n=−∞∑∣x∣PX(n)
- 注: ∣ x ∣ |x| ∣x∣表示取整
- 相互转化EX1: P M F → C D F PMF\to CDF PMF→CDF

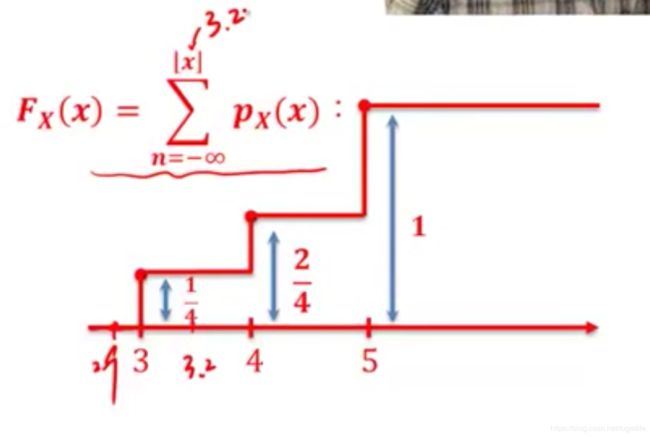
- 相互转化EX2: C D F → P M F CDF \to PMF CDF→PMF

阶梯前后的值相减
P X ( x ) = F X ( x + − x − ) P_X(x) = F_X(x^+-x^-) PX(x)=FX(x+−x−)

- 概率分布(probability Distribution)
任何一个 P M F PMF PMF或是之后介绍的 P D F PDF PDF都当作是一种概率分布(将总和为1的概率分布在点上)
4.4 离散概率分布(discrete probability distributions)
丢硬币:非正即反,正面概率为0.5
阿宅告白:非成功,即失败,成功概率为0.7
出门天气:非晴天即雨天,晴天概率为0.6
相似点:1次实验,两种结果。
只在意某一种结果是否发生 ⇒ \Rightarrow ⇒Bernoulli概率分布
4.4.1 Bernoulli概率分布(伯努利分布)
- 举例
- PMF:若实验成功几率为0.6,做一次实验, X X X代表成功次数。记为 X ∼ B e r n o u l l i ( 0.6 ) X\sim Bernoulli(0.6) X∼Bernoulli(0.6)
p X ( x ) = { 0.6 , x = 1 , 0.4 , x = 0 , 0 , o t h e r w i s e . p_X(x)=\left\{ \begin{aligned} 0.6 \quad &,x=1, \\ 0.4 \quad & ,x=0, \\ 0 \quad & ,otherwise. \end{aligned} \right. pX(x)=⎩⎪⎨⎪⎧0.60.40,x=1,,x=0,,otherwise. - CDF: F X ( x ) = ∑ n = − ∞ ∣ x ∣ p X ( x ) F_X(x)=\sum_{n=-\infty}^{|x|}p_X(x) FX(x)=∑n=−∞∣x∣pX(x)
F X ( x ) = { 0 , x < 0 , 0.4 , 0 ≤ x < 1 , 1 , x ≥ 1. F_X(x)=\left\{ \begin{aligned} 0 \quad &,x<0, \\ 0.4 \quad & ,0\le x<1, \\ 1 \quad & ,x \ge 1. \end{aligned} \right. FX(x)=⎩⎪⎨⎪⎧00.41,x<0,,0≤x<1,,x≥1.
- PMF:若实验成功几率为0.6,做一次实验, X X X代表成功次数。记为 X ∼ B e r n o u l l i ( 0.6 ) X\sim Bernoulli(0.6) X∼Bernoulli(0.6)
- 一般化
- PMF:若实验成功几率为 p p p,做1次实验, X X X代表成功次数。记为 X ∼ B e r n o u l l i ( p ) X\sim Bernoulli(p) X∼Bernoulli(p)
p X ( x ) = { p , x = 1 , 1 − p , x = 0 , 0 , o t h e r w i s e . p_X(x)=\left\{ \begin{aligned} p \quad &,x=1, \\ 1-p \quad & ,x=0, \\ 0 \quad & ,otherwise. \end{aligned} \right. pX(x)=⎩⎪⎨⎪⎧p1−p0,x=1,,x=0,,otherwise. - CDF: F X ( x ) = ∑ n = − ∞ ∣ x ∣ p X ( x ) F_X(x)=\sum_{n=-\infty}^{|x|}p_X(x) FX(x)=∑n=−∞∣x∣pX(x)
F X ( x ) = { 0 , x < 0 , 1 − p , 0 ≤ x < 1 , 1 , x ≥ 1. F_X(x)=\left\{ \begin{aligned} 0 \quad &,x<0, \\ 1-p \quad & ,0\le x<1, \\ 1 \quad & ,x \ge 1. \end{aligned} \right. FX(x)=⎩⎪⎨⎪⎧01−p1,x<0,,0≤x<1,,x≥1.
- PMF:若实验成功几率为 p p p,做1次实验, X X X代表成功次数。记为 X ∼ B e r n o u l l i ( p ) X\sim Bernoulli(p) X∼Bernoulli(p)
4.4.2 Binomial概率分布(二项分布)
EX1:阿宅鼓起勇气搭讪10人,若每次搭讪成功几率为0.6,10次成功8次的概率为?
EX2:艺洲五天午餐在某一餐厅就餐,若每次上菜超时的概率为0.9,5天中有3天超时的概率为?
共同点:做n次实验,同一个概率,只关注n次实验出现某结果k次之概率 ⇒ \Rightarrow ⇒Binomial概率分布
- 举例
- PMF:若实验成功几率为0.6,做10次实验, X X X代表成功次数。记为 X ∼ B I N ( 10 , 0.6 ) X\sim BIN(10,0.6) X∼BIN(10,0.6)
p X ( 8 ) = P ( X = 8 ) = ( 10 8 ) 0. 6 8 ( 1 − 0.6 ) 10 − 8 p_X(8)=P(X=8)=\binom{10}{8}0.6^8(1-0.6)^{10-8} pX(8)=P(X=8)=(810)0.68(1−0.6)10−8 - CDF: F X ( x ) = ∑ n = − ∞ ∣ x ∣ p X ( x ) F_X(x)=\sum_{n=-\infty}^{|x|}p_X(x) FX(x)=∑n=−∞∣x∣pX(x)
F X ( x ) = ∑ m = − ∞ ∣ x ∣ ( 10 m ) 0. 6 m ( 1 − 0.6 ) n − m F_X(x)=\sum_{m=-\infty}^{|x|}\binom{10}{m}0.6^m(1-0.6)^{n-m} FX(x)=m=−∞∑∣x∣(m10)0.6m(1−0.6)n−m
- PMF:若实验成功几率为0.6,做10次实验, X X X代表成功次数。记为 X ∼ B I N ( 10 , 0.6 ) X\sim BIN(10,0.6) X∼BIN(10,0.6)
- 一般化
- PMF:若实验成功几率为p,做n次实验, X X X代表成功次数。记为 X ∼ B I N ( n , p ) X\sim BIN(n,p) X∼BIN(n,p)
p X ( x ) = P ( X = x ) = ( n x ) p x ( 1 − p ) n − x p_X(x)=P(X=x)=\binom{n}{x}p^x(1-p)^{n-x} pX(x)=P(X=x)=(xn)px(1−p)n−x - CDF: F X ( x ) = ∑ n = − ∞ ∣ x ∣ p X ( x ) F_X(x)=\sum_{n=-\infty}^{|x|}p_X(x) FX(x)=∑n=−∞∣x∣pX(x)
F X ( x ) = ∑ m = − ∞ ∣ x ∣ ( n m ) p m ( 1 − p ) n − m F_X(x)=\sum_{m=-\infty}^{|x|}\binom{n}{m}p^m(1-p)^{n-m} FX(x)=m=−∞∑∣x∣(mn)pm(1−p)n−m
- PMF:若实验成功几率为p,做n次实验, X X X代表成功次数。记为 X ∼ B I N ( n , p ) X\sim BIN(n,p) X∼BIN(n,p)
4.4.3 Uniform概率分布(均匀分布)
EX1:丢一个公平的骰子:1-6各点出现的概率均等
EX2:混哥考试,作答A,B,C,D的概率均等
EX3:狡兔三窟,出现在三个窟的概率均等
共同点:一次实验,n种结果,个结果概率均等,关注某结果是否发生 ⇒ \Rightarrow ⇒Uniform概率分布
- 举例
-
PMF:如果 X X X等于 3 , 4 , 5 , 6 , 7 3, 4,5,6,7 3,4,5,6,7的概率均等。记为 X ∼ U N I F ( 3 , 7 ) X\sim UNIF(3,7) X∼UNIF(3,7)
p X ( x ) = { 1 7 − 3 + 1 , x = 3 , 4 , 5 , 6 , 7 , 0 , o t h e r w i s e . p_X(x)=\left\{ \begin{aligned} \frac{1}{7-3+1} \quad &,x=3,4,5,6,7, \\ 0 \quad & ,otherwise. \end{aligned} \right. pX(x)=⎩⎨⎧7−3+110,x=3,4,5,6,7,,otherwise. -
CDF: F X ( x ) = ∑ n = − ∞ ∣ x ∣ p X ( x ) F_X(x)=\sum_{n=-\infty}^{|x|}p_X(x) FX(x)=∑n=−∞∣x∣pX(x)
-
F X ( x ) = { 0 , x < 3 , ∣ x ∣ − 3 + 1 6 , 3 ≤ x < 8 , 1 , x ≥ 8. F_X(x)=\left\{ \begin{aligned} 0 \quad &,x<3, \\ \frac{|x|-3+1}{6} \quad & ,3\le x<8, \\ 1 \quad & ,x \ge 8. \end{aligned} \right. FX(x)=⎩⎪⎪⎪⎨⎪⎪⎪⎧06∣x∣−3+11,x<3,,3≤x<8,,x≥8.
- 一般
-
PMF:如果 X X X等于 a , a + 1 , … , b a,a+1,\dots,b a,a+1,…,b的概率均等。记为 X ∼ U N I F ( a , b ) X\sim UNIF(a,b) X∼UNIF(a,b)
p X ( x ) = { 1 b − a + 1 , x = a , a + 1 , … , b , 0 , o t h e r w i s e . p_X(x)=\left\{ \begin{aligned} \frac{1}{b-a+1} \quad &,x=a,a+1,\dots,b, \\ 0 \quad & ,otherwise. \end{aligned} \right. pX(x)=⎩⎨⎧b−a+110,x=a,a+1,…,b,,otherwise. -
CDF: F X ( x ) = ∑ n = − ∞ ∣ x ∣ p X ( x ) F_X(x)=\sum_{n=-\infty}^{|x|}p_X(x) FX(x)=∑n=−∞∣x∣pX(x)
-
F X ( x ) = { 0 , x < a , ∣ x ∣ − a + 1 b − a + 1 , a ≤ x < b , 1 , x ≥ b . F_X(x)=\left\{ \begin{aligned} 0 \quad &,x<a, \\ \frac{|x|-a+1}{b-a+1} \quad & ,a\le x<b, \\ 1 \quad & ,x \ge b. \end{aligned} \right. FX(x)=⎩⎪⎪⎪⎨⎪⎪⎪⎧0b−a+1∣x∣−a+11,x<a,,a≤x<b,,x≥b.
4.4.4 学这些概率分布有什么用
-
很多事物背后概率模型是未知的
-
对事物的运作方式、本质清楚后,若跟某概率分布的本质相同或是接近,我们便可采用该概率分布来近似、模拟该事物的运作
-
在这近似、模拟的概率模型上,便可以开始估算各式各样事件的概率。
-
视频地址在上方(有需要可以留言要云分享)
-
如有不妥,请指示正,谢谢阅读!
作者:togetlife