关键路径算法

1、拓扑排序的意义？

举个例子先：一个软件专业的学生学习一系列的课程，其中一些课程必须再学完它的基础的先修课程才能开始。如：在《程序设计基础》和《离散数学》学完之前就不能开始学习《数据结构》。这些先决条件定义了课程之间的领先(优先)关系。这个关系可以用有向图更清楚地表示。图中顶点表示课程，有向边表示先决条件。若课程i是课程j的先决条件，则图中有弧。若要对这个图中的顶点所表示的课程进行拓扑排序的话，那么排序后得到的序列，必须是按照先后关系进行排序，具有领先关系的课程必然排在以它为基础的课程之前，若上例中的《程序设计基础》和《离散数学》必须排在《数据结构》之前。进行了拓扑排序之后的序列，称之为拓扑序列。

2、关键路径的定义：

路径上各个活动所持续的时间之和称为路径长度，从源点到汇点具有最大长度的路径叫关键路径。

3、如何实现关键路径？

辨别关键活动就是要找e(i)=l(i)的活动。为了求得e(i)和l(i)，首先应求得事件的最早发生时间ve(j)和最迟发生时间vl(j)。如果活动ai由弧表示，其持续时间记为dut()，则有如下关系
e(i) = ve(j)
l(i) = vl(k) - dut()
求解ve(j)和vl(j)需分两个步进行：
1） 从ve(0)=0开始向前推进求得ve(j)
Ve(j) = Max{ve(i) + dut() };属于T，j=1,2...,n-1
其中T是所有以第j个顶点为头的弧的集合。

2） 从vl(n-1) = ve(n-1)起向后推进求得vl(j)
vl(i) = Min{vl(j) - dut(};属于S，i=n-2,...,0
其中，S是所有以第i个顶点为尾的弧的集合。
这两个递推公式的计算必须分别在拓扑有序和逆拓扑有序的前提先进行。也就是说，ve(j-1)必须在vj的所有前驱的最早发生时间求得之后才能确定，而vl(j-1)必须在Vj的所有后继的最迟发生时间求得之后才能确定。因此可以在拓扑排序的基础上计算ve(j-1)和vl(j-1)。

4、关键路径算法

首先定义全局变量：

其中stack2用来存储拓扑排序列，已便后面求关键路径时使用。

上述代码周浩，除了加粗部分外，与前面的的拓扑排序算法没有什么不同的。

下面来看关键路径的算法代码。

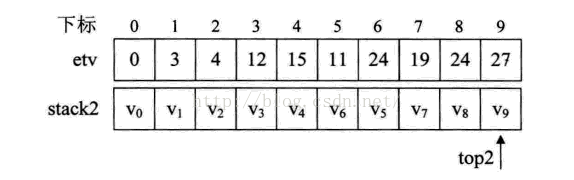
1、第6行，调用求拓扑序列的函数，求出etv，和栈stack的值如下，

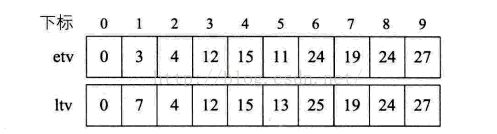
2、当程序执行到第20行时，etv[1]=3,ltv[1]=7,表示v1这件事在第7天才开始，也可以保证整个工程的按期完成，v1也可以提前开始，但最早也只能在第3天开始。

3、所以就是判断ete与lte是否相等，相等意味着活动没有任何空闲，是关键活动时间，否则就不是，最后的关键路径如下。

个人总结：

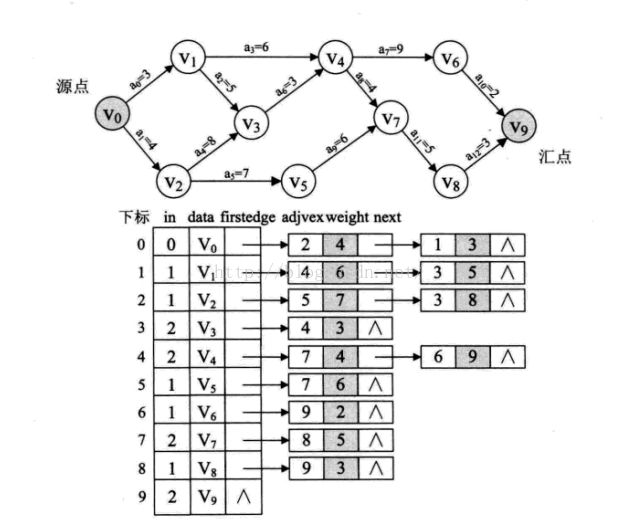
最长的一条路径就是关键路径,因为图中每个活动都是必须的，只有最长的工期完成后，项目才真正完成了，图中4+8+3+4+5+3=27 也就是v0-v2-v3-v4-v7-v8-v9 ，显然是最长的，所以为关键路径。

从左边开始每个活动所需要最长的时间就是最早开始时间，如v1，只有v0指向它，那么最早开始时间就是3；相对于v3，v0->v2->v3
4+8=12，v0->v1->v3 3+5+8,两者比较，前者大，故12为最早开始时间，依次类推。

从右边倒推，可以求的最迟开始时间，如v9为27，以v8为例，v8->v9 倒推 27-3=24 所以I最迟开始时间为24；v4为例，v4->v7->v8->v9 倒推27-3-5-415=39，v4->v6->v9 倒推 27-2-9=16，两者取最小的，所以v4的最迟开始时间为15。

代码设计：

1、在结点的定义中增加ee和le 字段用于记录个事件的最早开始时间和最迟开始时间，同时得到关键路径和最小工期

2、邻接矩阵中使用边权代替原来连接标志1

3、进行拓扑排序，形成拓扑序列

1 2 3 4 5 6 7 8 9

4、按拓扑序列顺序，从前向后搜索寻找个活动（即边），若存在该活动，则计算相应事件的最早开始时间。

5、按拓扑序列顺序，从后向前搜索寻找个活动（即边），若存在该活动，则计算相应事件的最迟开始时间。

6、计算各活动的最早开始时间和最迟开始时间

#include   
#include   
#define MaxVerNum 20  
   
int visited[MaxVerNum];  
   
typedef char VertexType;  
   
typedef struct ArcNode  
{  
       int adjvex;                                         //该弧指向的顶点位置  
       struct ArcNode * nextarc;          //指向下一个表结点  
       int info;                                      //权值信息  
}ArcNode;                                              //边结点类型  
   
typedef struct VNode  
{  
       VertexType data;  
       int indegree;  
       ArcNode * firstarc;  
}VNode, Adjlist[MaxVerNum];  
   
typedef struct  
{  
       Adjlist vertices;            //邻接表  
       int vernum, arcnum;             //顶点数和弧数  
}ALGraph;  
   
//查找符合的数据在数组中的下标  
int LocateVer(ALGraph G, char u)  
{  
       int i;  
       for(i = 0; i < G.vernum; i++)  
       {  
              if(u == G.vertices[i].data)  
                     return i;  
       }  
       if(i == G.vernum)  
       {  
              printf("Error u!\n");  
              exit(1);  
       }  
       return 0;  
}  
   
//常见图的邻接矩阵  
void CreateALGraph(ALGraph &G)  
{  
       int i, j, k, w;  
       char v1, v2;  
       ArcNode * p;  
       printf("输入顶点数和弧数: ");  
       scanf("%d %d", &G.vernum, &G.arcnum);  
       printf("请输入顶点!\n");  
       for(i = 0; i < G.vernum; i++)  
       {  
              printf("请输入第 %d 个顶点: \n", i);  
              fflush(stdin);  
              scanf("%c", &G.vertices[i].data);  
              G.vertices[i].firstarc = NULL;  
              G.vertices[i].indegree = 0;  
       }  
   
       for(k = 0; k < G.arcnum; k++)  
       {  
              printf("请输入弧的顶点和相应权值(v1, v2, w): \n");  
              //清空输入缓冲区  
              fflush(stdin);  
              scanf("%c %c %d", &v1, &v2, &w);  
              i = LocateVer(G, v1);  
              j = LocateVer(G, v2);  
              p = (ArcNode *)malloc(sizeof(ArcNode));  
              p->adjvex = j;  
              p->info = w;  
              p->nextarc = G.vertices[i].firstarc;  
              G.vertices[i].firstarc = p;  
              G.vertices[j].indegree++;                   //vi->vj, vj入度加1  
       }  
       return;  
}  
   
//求图的关键路径函数  
void CriticalPath(ALGraph G)  
{  
       int i, k, e, l;  
       int * Ve, * Vl;  
       ArcNode * p;  
   
       //*****************************************  
       //以下是求时间最早发生时间  
       //*****************************************  
   
       Ve = new int [G.vernum];  
       Vl = new int [G.vernum];  
   
       for(i = 0; i < G.vernum; i++)              //前推  
              Ve[i] = 0;  
   
       for(i = 0; i < G.vernum; i++)  
       {  
              ArcNode * p = G.vertices[i].firstarc;  
              while(p != NULL)  
              {  
                     k = p->adjvex;  
                     if(Ve[i] + p->info > Ve[k])  
                            Ve[k] = Ve[i]+p->info;  
                     p = p->nextarc;  
              }  
       }  
       //*****************************************  
       //以下是求最迟发生时间  
       //*****************************************  
       for(i = 0; i < G.vernum; i++)  
              Vl[i] = Ve[G.vernum-1];  
       for(i = G.vernum-2; i >= 0; i--)                 //后推  
       {  
              p = G.vertices[i].firstarc;  
              while(p != NULL)  
              {  
                     k = p->adjvex;  
                     if(Vl[k] - p->info < Vl[i])  
                            Vl[i] = Vl[k] - p->info;  
                     p = p->nextarc;  
              }  
       }  
       //******************************************  
       for(i = 0; i < G.vernum; i++)  
       {  
              p = G.vertices[i].firstarc;  
              while(p != NULL)  
              {  
                     k = p->adjvex;  
                     e = Ve[i];              //最早开始时间为时间vi的最早发生时间  
                     l = Vl[k] - p->info;             //最迟开始时间  
                     char tag = (e == l) ? '*' : ' '; //关键活动  
                     printf("(%c, %c), e = %2d, l = %2d, %c\n", G.vertices[i].data, G.vertices[k].data, e, l, tag);  
                     p = p->nextarc;  
              }  
       }  
       delete [] Ve;  
       delete [] Vl;  
}  
   
void main()  
{  
       ALGraph G;  
       printf("以下是查找图的关键路径的程序。\n");  
       CreateALGraph(G);  
       CriticalPath(G);  
}