利用C语言实现二叉搜索树的遍历、查找、插入、删除
IDE:codebloks,编译器:gcc5.1.0
二叉搜索树和我们通常的二叉树还是有一定的区别,顾名思义,一颗二叉搜索树以一颗二叉树来组织,其中每一个结点就是一个对象。除了key(关键字)和卫星数据外,每个节点还包括left(左孩子指针)、right(右孩子指针)和p。如果孩子结点不存在则为NULL。
二叉搜索树的性质如下:
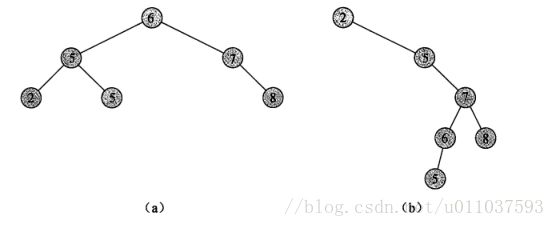
设x是二叉搜索树中的一个结点。如果y是x的左子树中的一个结点,那么y.key≤x.key。如果y是x右子树中的一个结点,那么y.key≥x.key。图a和b正好说明了这一点。
二叉搜索树的遍历有三种,分别为先序遍历(perorder tree walk)、中序遍历(inorder tree walk)、后续遍历(postorder tree walk)。
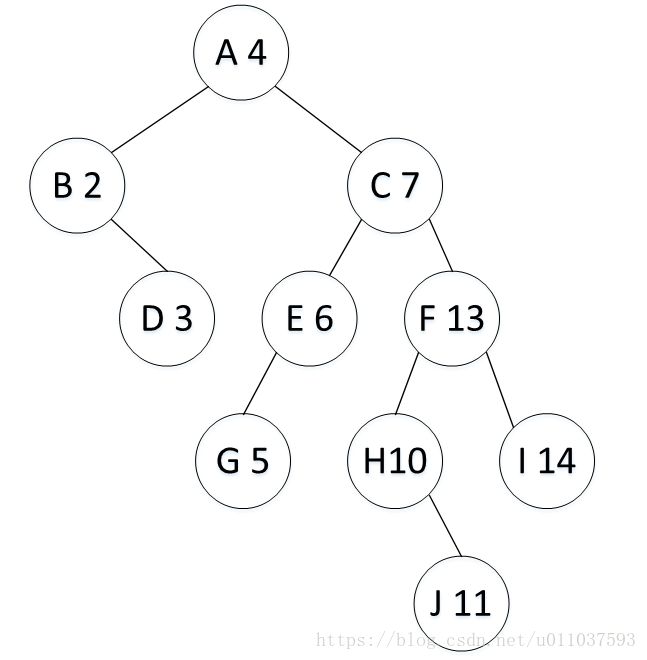
1.首选定义二叉搜索树结点的数据结构,为了简单期间,只定义了关键字,左孩子和右孩子指针本例子中的二叉搜索树如图c所示:
#include 2.下面分别是三种遍历的C语言实现。唯一不同的地方是输出关键字的位置不void PreTraverseBSTree(pBstNode pBST)
void PreTraverseBSTree(struct BSTNode *pBST)
{
if(NULL != pBST)
{
printf("数据为:%d,父节点地址为:%p\n",pBST ->data,pBST ->pParent);
if(NULL != pBST ->pLchild )
PreTraverseBSTree(pBST ->pLchild);
if(NULL != pBST ->pRchild)
PreTraverseBSTree(pBST ->pRchild);
}
}
void InTraverseBSTree(struct BSTNode *pBST)
{
if(NULL != pBST)
{
if(NULL != pBST ->pLchild )
PreTraverseBSTree(pBST ->pLchild);
printf("数据为:%d,父节点地址为:%p\n",pBST ->data,pBST ->pParent);
if(NULL != pBST ->pRchild)
PreTraverseBSTree(pBST ->pRchild);
}
}
void PostTraverseBSTree(struct BSTNode *pBST)
{
if(NULL != pBST)
{
if(NULL != pBST ->pLchild )
PreTraverseBSTree(pBST ->pLchild);
if(NULL != pBST ->pRchild)
PreTraverseBSTree(pBST ->pRchild);
printf("数据为:%d,父节点地址为:%p\n",pBST ->data,pBST ->pParent);
}
}3.下面是查找的C语言实现。第一个版本是自己实现的,在写的过程中,想到了是不是可以去掉return,去掉return编译器报警,经过一番查找资料和思考,发现有没有return不会影响结果,报警的原因是SearchBSTree()的返回值类型是pBstNode,如果去掉return就没有返回值,类型不匹配就会报警。版本1没有版本2效率高,版本2没有版本3效率高,版本2和版本3参考自《算法导论》。版本3采用了while循环展开递归,用一种迭代方式重写这个过程。对于大多数计算机,迭代版本的效率要高很多。
//查找成功返回该结点的地址,失败返回NULL
struct BSTNode *SearchBSTree(struct BSTNode *pBST,int key) //版本1
{
if(NULL == pBST)
return NULL;
else if(key < pBST ->data)
return SearchBSTree(pBST ->pLchild,key);
else if(key > pBST ->data)
return SearchBSTree(pBST ->pRchild,key);
else return pBST;
}
struct BSTNode *SearchBSTree(struct BSTNode *pBST,int key) //版本2
{
if(NULL == pBST || key == pBST ->data)
return pBST;
else if(key < pBST ->data)
return SearchBSTree(pBST ->pLchild,key);
else return SearchBSTree(pBST ->pRchild,key);
}
struct BSTNode *SearchBSTree(struct BSTNode *pBST,int key) //版本3
{
while(NULL != pBST && key != pBST ->data)
{
if(key < pBST ->data)
pBST = pBST ->pLchild;
else pBST = pBST ->pRchild;
}
return pBST;
}4.在二叉搜索树中寻找最大值和最小值。由二叉搜索树的性质可知,我们总能在二叉搜索树中找到一个元素,两个拥有相同父结点的子结点中,左结子点的值肯定小于父节点,也小于右子结点,所以最小值总在二叉搜索树的左子树中,最大值总在右子树中。实现的代码如下:时间复杂度为O(h)。
struct BSTNode *SearchMinBSTree(struct BSTNode *pBST,int *pMinData)//查找二叉搜索树中最小的值
{
while(NULL != pBST ->pLchild)
{
pBST = pBST ->pLchild;
}
*pMinData = pBST ->data;
return pBST;
}
struct BSTNode *SearchMaxBSTree(struct BSTNode *pBST,int *pMaxData) //查找二叉搜索树中最大的值
{
while(NULL != pBST ->pRchild)
{
pBST = pBST ->pRchild;
}
*pMaxData = pBST ->data;
return pBST;
}5.向二叉树中插入一个元素
void InsertBSTree(struct BSTNode *pBST,int InsertVal) //插入元素
{
struct BSTNode *pRoot = pBST;//记录根节点地址
struct BSTNode *pNew = (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pNew)
exit(-1);
pNew ->data = InsertVal;
pNew ->pLchild = pNew ->pRchild = NULL;
struct BSTNode *pTmp = NULL;
while(NULL != pBST )
{
pTmp = pBST;
if(pNew ->data < pBST ->data)
pBST = pBST ->pLchild;
else
pBST = pBST ->pRchild;
}
pNew->pParent = pTmp;
if(NULL == pTmp) //当树为空时,将插入节点的地址赋给根节点
*pRoot = *pNew;
else if(pNew ->data <= pTmp ->data)
pTmp ->pLchild = pNew;
else
pTmp ->pRchild = pNew;
}6.删除二叉树中的元素
void DeleteBSTree(struct BSTNode *pBST,int DeleteVal)
{
struct BSTNode *pTem = SearchBSTree(pBST,DeleteVal);
if(pTem == NULL)
{
printf("没有找到要删除的元素!\n");
exit(-1);
}
if(NULL == pTem ->pLchild && NULL == pTem ->pRchild) //删除节点无左右孩子
{
if(pTem == pTem ->pParent ->pLchild) //删除节点是其父节点的左孩子
{
pTem ->pParent ->pLchild = NULL;
}
else //删除节点是其父节点的右孩子
{
pTem ->pParent ->pRchild =NULL;
}
free(pTem);
pTem = NULL;
}
else if(NULL == pTem ->pLchild) //删除节点无左孩子
{
if(pTem == pTem ->pParent ->pLchild) //删除节点为其父节点的左孩子
{
pTem ->pParent ->pLchild = pTem ->pRchild;
pTem ->pRchild ->pParent =pTem ->pParent;
}
else //删除节点为其父节点的右孩子
{
pTem ->pParent ->pRchild = pTem ->pRchild;
pTem ->pRchild ->pParent =pTem ->pParent;
}
free(pTem);
pTem = NULL;
}
else if(NULL == pTem ->pRchild) //删除节点无右孩子
{
if(pTem == pTem ->pParent->pLchild) //删除节点为其父节点的左孩子
{
pTem ->pParent ->pLchild = pTem ->pLchild;
pTem ->pLchild ->pParent = pTem ->pParent;
}
else //删除节点为其父节点的右孩子
{
pTem ->pParent ->pRchild = pTem ->pLchild;
pTem ->pLchild ->pParent = pTem ->pParent;
}
free(pTem);
pTem = NULL;
}
else //删除节点有左右孩子,用删除节点左字树中的最大值或者右子树中最小值来代替删除节点
//本例中用右子树中最小值来代替
{
struct BSTNode *pTial = pTem ->pRchild;
while(NULL != pTial ->pLchild) //查找右子树中的最小值
{
pTial = pTial ->pLchild;
}
if(pTem == pTial ->pParent) //右子树中的最小值的父节点是删除节点
{
if(pTem == pTem ->pParent ->pLchild) //删除节点为其父节点的左孩子
{
pTem ->pParent ->pLchild = pTial;
pTial ->pLchild = pTem ->pLchild;
pTem ->pLchild->pParent = pTial;
}
else
{
pTem ->pParent ->pRchild = pTial;
pTial ->pLchild = pTem ->pLchild;
pTem ->pLchild->pParent = pTial;
}
free(pTem);
pTem = NULL;
}
else
{
pTial ->pRchild ->pParent = pTial ->pParent;
pTial ->pParent ->pLchild = pTial ->pRchild;
pTial ->pParent ->pParent = pTial;
pTial ->pRchild = pTial ->pParent;
pTial ->pLchild = pTem ->pLchild;
pTem ->pLchild ->pParent = pTial;
if(pTem == pTem ->pParent ->pLchild)
{
pTem ->pParent ->pLchild = pTial;
}
else
pTem ->pParent ->pRchild = pTial;
free(pTem);
pTem = NULL;
}
}
}7.创建一颗二叉搜索树
struct BSTNode *CreateBSTree(void)
{
struct BSTNode * pA = (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pA)
exit(-1);
struct BSTNode * pB= (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pB)
exit(-1);
struct BSTNode * pC= (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pC)
exit(-1);
struct BSTNode * pD= (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pD)
exit(-1);
struct BSTNode * pE= (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pE)
exit(-1);
struct BSTNode * pF= (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pF)
exit(-1);
struct BSTNode * pG= (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pG)
exit(-1);
struct BSTNode * pH= (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pH)
exit(-1);
struct BSTNode * pI= (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pI)
exit(-1);
struct BSTNode * pJ= (struct BSTNode *)malloc(sizeof(struct BSTNode));
if(NULL == pJ)
exit(-1);
pA ->data = 4;
pB ->data = 2;
pC ->data = 7;
pD ->data = 3;
pE ->data = 6;
pF ->data = 13;
pG ->data = 5;
pH ->data = 10;
pI ->data = 14;
pJ ->data = 11;
pA ->pParent = NULL;
pA ->pLchild = pB;
pA ->pRchild = pC;
pB ->pParent = pA;
pB ->pLchild = NULL;
pB ->pRchild = pD;
pD ->pParent = pB;
pD ->pLchild = pD ->pRchild = NULL;
pC ->pParent = pA;
pC ->pLchild = pE;
pC ->pRchild = pF;
pE ->pParent = pC;
pE ->pLchild = pG;
pE ->pRchild = NULL;
pF ->pParent = pC;
pF ->pRchild = pI;
pF ->pLchild =pH;
pG ->pParent = pE;
pG ->pLchild = pG ->pRchild = NULL;
pH ->pParent = pF;
pH ->pLchild = NULL;
pH ->pRchild = pJ;
pI ->pParent = pF;
pI ->pLchild = pI ->pRchild = NULL;
pJ ->pParent = pH;
pJ ->pLchild = pJ ->pRchild =NULL;
return pA;
}8.主函数
int main()
{
int MinData,MaxData;
struct BSTNode *pRoot;
pRoot=CreateBSTree();
//printf("先序遍历:\n");
//PreTraverseBSTree(pRoot);
printf("\n中序遍历:\n");
InTraverseBSTree(pRoot);
//printf("\n后续遍历:\n");
//PostTraverseBSTree(pRoot);
printf("\n查找的元素为: key = 5");
struct BSTNode *pKeyNode = SearchBSTree(pRoot,5);
if(NULL == pKeyNode)
printf("查找失败!\n");
else
printf("\n查找成功,结点地址为:%p!",pKeyNode);
struct BSTNode *pMinData = SearchMinBSTree(pRoot,&MinData);
printf("\n最小值为:%d,其结点地址为:%p",MinData,pMinData);
struct BSTNode *pMaxDate = SearchMaxBSTree(pRoot,&MaxData);
printf("\n最大值为:%d,其结点地址为:%p",MaxData,pMaxDate);
printf("\n插入的元素为: data = 10");
InsertBSTree(pRoot,1); //插入元素
printf("\n中序遍历:\n");
InTraverseBSTree(pRoot);
DeleteBSTree(pRoot,4);
printf("\n中序遍历:\n");
InTraverseBSTree(pRoot);
return 0;
}9.运行结果
中序遍历:
数据为:2,父节点地址为:00e11700
数据为:3,父节点地址为:00e11718
数据为:4,父节点地址为:00000000
数据为:7,父节点地址为:00e11700
数据为:6,父节点地址为:00e11730
数据为:5,父节点地址为:00e11760
数据为:13,父节点地址为:00e11730
数据为:10,父节点地址为:00e11778
数据为:11,父节点地址为:00e117a8
数据为:14,父节点地址为:00e11778
查找的元素为: key = 5
查找成功,结点地址为:00e11790!
最小值为:2,其结点地址为:00e11718
最大值为:14,其结点地址为:00e117c0
插入的元素为: data = 10
中序遍历:
数据为:2,父节点地址为:00e11700
数据为:1,父节点地址为:00e11718
数据为:3,父节点地址为:00e11718
数据为:4,父节点地址为:00000000
数据为:7,父节点地址为:00e11700
数据为:6,父节点地址为:00e11730
数据为:5,父节点地址为:00e11760
数据为:13,父节点地址为:00e11730
数据为:10,父节点地址为:00e11778
数据为:11,父节点地址为:00e117a8
数据为:14,父节点地址为:00e11778
中序遍历:
数据为:2,父节点地址为:00e11700
数据为:1,父节点地址为:00e11718
数据为:3,父节点地址为:00e11718
数据为:4,父节点地址为:00000000
数据为:10,父节点地址为:00e11778
数据为:6,父节点地址为:00e117a8
数据为:5,父节点地址为:00e11760
数据为:13,父节点地址为:00e117a8
数据为:11,父节点地址为:00e11778
数据为:14,父节点地址为:00e11778