经典卷积神经网络 之 VGG
VGGnet
牛津大学 Visual Geometry Group(视觉几何组)的同志写的论文,所以叫VGG
时间:
2014年
出处:
Very Deep Convolutional Networks forLarge-Scale Image Recognition
论文的翻译:http://blog.csdn.net/roguesir/article/details/77470043
目的:
探究在大规模图像识别任务中,卷积网络的深度与其性能之间的关系
做法:
VGG把 Alexnet 最开始的一个7*7的卷积核用 3个3*3的卷积核代替。
通过反复堆叠3*3的小型卷积核(stride:1,padding:1)和 2*2的最大池化层,不断加深网络结构来提升性能,成功地构筑了16~19层深的卷积神经网络。
为什么这么做?
(1)3x3是最小的能够捕获左、右、上、下和中心概念的尺寸;
(2)AlexNet最开始的7*7的卷积核的感受野是:7*7
……..VGG第一个卷积核的感受野:3*3
……..第二个卷积核的感受野:(3-1)*1+3=5
……..第三个卷积核的感受野:(5-1)*1+3=7
……..可见三个3*3卷积核和一个7*7卷积核的感受野是一样的,但是3*3卷积核可以把网络做的更深。
(3)多个3*3的卷积层比一个大尺寸的filter卷积层有更多的非线性,使得判决函数更加具有判断性。
(4)多个3*3的卷积层比一个大尺寸的filter具有更少的参数。
成就:
VGGNet 相比之前state-of-the-art的网络结构,错误率大幅下降, 获得ILSVRC 2014比赛分类项目的第2名和定位项目的第1名。
贡献:
证明了使用很小的卷积(3*3),增加网络深度可以有效提升模型的效果,而且VGGNet对其他数据集具有很好的泛化能力
VGG的结构
为了在公平的原则下探究网络深度对模型精确度的影响,所有卷积层有相同的配置:
卷积核大小为3*3,步长为1(stride:1),填充为1(padding:1);
共有5个最大池化层,大小都为2*2,步长为2(stride:2);
三个全连接层,前两层都有4096通道,第三层共1000路及代表1000个标签类别;最后一层为softmax层;
所有隐藏层后都带有ReLU非线性激活函数;
下图为VGG16的结构图:
![]()
配置对比:
![]()
这张图的意思是他们一共建了A, B, C, D, E, F 6个不同的网络。
结构A:和AlexNet类似,卷积层分为了5个stage,全连接层还是3层。只不过卷积层用的都是3x3大小的filter,具体的细节我会在下文接着阐述。
结构A-LRN:保留AlexNet里面LRN操作,其他与结构A无区别。
结构B:在A的 stage2 和 stage3 分别增加一个3*3的卷积层,共有10个卷积层,全连接层还是3层。
结构C:在B的基础上,stage3,stage4,stage5分别增加一个1*1的卷积层,有13个卷积层,全连接层还是3层,总计16层。
结构D:在C的基础上,stage3,stage4,stage5分别增加一个3*3的卷积层,有13个卷积层,全连接层还是3层,总计16层。
结构E:在D的基础上,stage3,stage4,stage5分别再增加一个3*3的卷积层,有16个卷积层,全连接层还是3层,总计19层。
参数(以VGG16为例):
![]()
VGG结构需要注意的点:
1、卷积核都是3x3的
2、参数最多的层:第一个全卷积层,占用内存最多的层:前两个卷积层
3、卷积核个数从64到128到256的目的:stride:1,padding:1 的卷积,特征图大小不变,但是进经过2*2的pooling操作,每个特征图的w和h都变为1/2,特征图的大小变为1/4,将卷积核的个数翻倍,可以降低信息衰减
4、使用了1*1卷积核,1*1卷积核有什么作用?
(1)降维( dimension reductionality )。比如,一张500 * 500且厚度depth为100 的图片在20个filter上做1*1的卷积,那么结果的大小为500*500*20。
(2)加入非线性。卷积层之后经过激励层,1*1的卷积在前一层的学习表示上添加了非线性激励( non-linear activation ),提升网络的表达能力;
训练:
图片预处理:
在训练集中的每个像素上减去RGB的均值
为了获得初始化的224x224大小的图片,通过在每张图片在每次随机梯度下降时进行一次裁减,为了更进一步的增加训练集,对每张图片进行水平翻转以及进行随机RGB色差调整。
初始对原始图片进行裁剪时,原始图片的最小边不宜过小,这样的话,裁剪到224x224的时候,就相当于几乎覆盖了整个图片,这样对原始图片进行不同的随机裁剪得到的图片就基本上没差别,就失去了增加数据集的意义,但同时也不宜过大,这样的话,裁剪到的图片只含有目标的一小部分,也不是很好。
针对上述裁剪的问题,提出的两种解决办法:
(1) 固定最小遍的尺寸为256
(2) 随机从[256,512]的确定范围内进行抽样,这样原始图片尺寸不一,有利于训练,这个方法叫做尺度抖动scal jittering,有利于训练集增强。 训练时运用大量的裁剪图片有利于提升识别精确率。
网络的训练一些相关细节:
网络采用常用的mini-batch 的梯度下降法进行网络的训练, size为256;
权值更新的原则也是常用的 momentum 的方法,动量值为0.9; 对网络的权值 decay 采用L2正则化方法,其中惩罚因子为5*10-4;
对最后的全连接层的前两层采用 dropout 机制, dropout的值为0.5;
网络的学习率的大体设置为:初始值为0.01,当进入plateau时(可以认为验证值的识别率不再变化,当然也可以选其它的,如:lossValue),学习率 缩小10倍,变为0.001,然后再重复一次,变为0.0001就OK了。
权值的初始化是一个重要的问题:
对于深层的网络来说,网络的权值初始值特别特别容易影响最后的识别率的
而相对于比较 shallow的网络的初始值,我们可以用随机初始化的方法解决。所以文中的做法就是随机初始化(用mean为0,variance为0.01的高斯分布)相当shallow的网络 A,然后训练完成了
当我们训练其它相当于较深的网络的时候,我们用网络A的权值来初始化其它网络的权值就OK了
在训练过程中,我们的学习率初始值同样保持为0.01
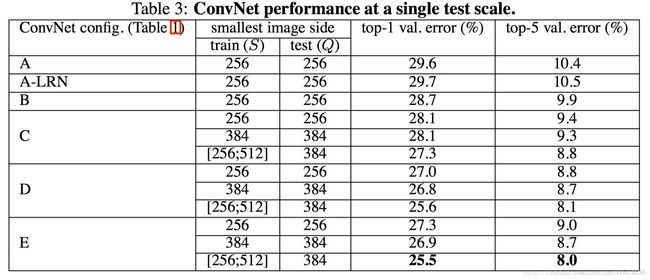
single-scale训练
测试图片尺寸固定为一个值时,各个模型运用在ILSVRC-2012数据集上的结果
top-1 error 就是实在的错误率,概率最大一类的作为输出;而top-5 error常作为 ILSVRC 官方的识别率的测试,它是指概率的前5个中只要有对应的正确的类就算是识别对了,没有就是错了
结论:
·A与A-LRN比较:A-LRN结果没有A好,说明LRN作用不大。
·A与B, C, D, E比较,A是这当中layer最少的,相比之下A效果不如B,C,D,E,说明Layer越深越好;
·B与C比较:增加 1*1 filter,增加了额外的非线性提升效果;
·C与D比较:3*3 的 filter(结构D)比 1*1(结构C)的效果好
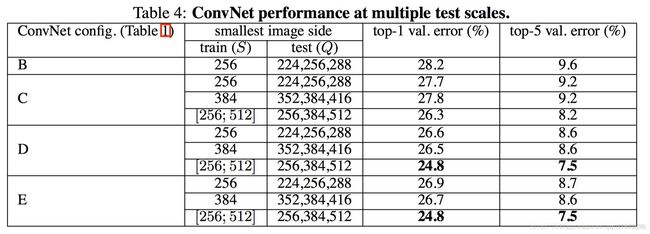
Multi-scale训练
方法1:single-scale训练 S,multi-scale测试 {S-32,S,S+32}
方法2:multi-scale训练[Smin;Smax],multi-scale测试{Smin,middle,Smax}
可以看到结果稍好于前者测试图片采用单一尺寸的效果
当取训练图片S利用尺度抖动的方法范围为[256;512],测试图片也利用尺度抖动取256,384,512三个值进行分类结果平均值,然后探究对测试图片进行多裁剪估计的方法,即对三个尺度上每个尺度进行50次裁剪(5x5大小的正常网格,并进行两次翻转)即总共150次裁剪的效果图,如下:
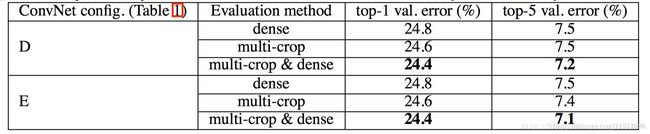
可以看到这个效果比之前两个效果更进一步,说明多尺度裁剪也起了一定好的作用。
模型融合
如果结合多个卷积网络的sofamax输出,分类效果会更好。