自动网络设计（NAS）Randomly Wired Neural Networks 何凯明团队

文章 iker peng（知乎：https://www.zhihu.com/people/ikerpeng/）原创，转载请与我联系～

 

 

作为AutoML的一个重要的分支， Neural Architecture Searching（NAS）越来越受到人们的关注。 大神何凯明也来了～ 今天介绍他们组近期的一个工作： Exploring RandomlyWired Neural Networks for Image Recognition。

说到NAS， 比较有影响力的相关研究要回到2016年 大牛Zoph & Quoc他们的工作【1】。他们将网络设计的问题看作是一个决策问题。 然后通过强化学习来解决。

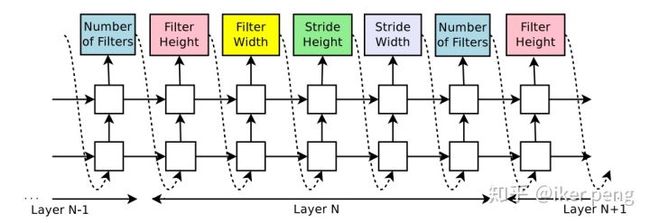
控制器输出网络参数

如图所示，在文章【1】当中，作者使用LSTM构造了一个控制器。这个控制器输出每一层网络的结构组成，如卷积核的大小步长等等。然后，通过输出的参数构造出一个真实的网络，在相应的任务当中得到一个performance的打分。此打分作为强化学习的反馈来训练控制器。

显然在这里控制器输出每一个结构序列都像是强化学习对应的一个动作，从网络得到的反馈便是该智能体的奖励。算法简单直观。由该算法设计的网络在16年的时候就超过了当时ResNet得到的最好的成绩。但是其最大的毛病就是浪费，最大的优势就是咱不差钱。为了得到这个结果他们花了3000+ GPU天的时间。这并不是一般人能够做的实验！

但是这个事说明了这条路的可行性。于是后期出现了很多相关的研究和改进。基本上集中在三个方面：搜索空间（search space），搜索策略（search strategy） 以及评价策略（Performance Evaluation）上。搜索空间，空间的设计基本上都采用了一个有向图来对网络结构进行建模，主流的方式都从整个网络的搜索变成了cell或者是block层面的搜索，然后再重复使用这些block来构建整个网络。策略上主要出现了演化算法（ES），梯度算法以及随机搜索等等。评价策略上变化不多，最常用的是one-shot architecture的方式。而我个人觉得有必要要提的是 DARTS这个工作【2】。

这个工作通过将一个离散的搜索空间变成连续的搜索空间引入了梯度优化的算法。然后通过交替执行search和train的方式来进行网络的搜索。此时达到同等于手工设计的网络的性能只需要 4天的时间了。惊艳！

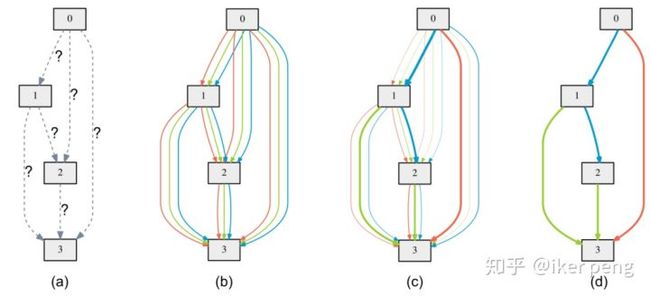
如图所示，文章同样是通过搜索cell的方式进行搜索。对于这个待搜索的cell，其中包含4个节点表示的是该cell当中的隐含层输出。那么该问题转化为搜索各个隐含层状态之间的连接关系，以及各个连接线的操作子（如convolution 3×3）。而单独的选择每一个操作子变成了加入所有操作子到连接线，并对所有操作子赋权值的操作。因此，搜索网络结构的问题变成了搜索操作子权重的问题。本文以一种十分高效的方式超过了人类设计的网络。

那么问题来了。为什么，这个网络当中用来model 网络结构的图长成这样勒？如本文要介绍的这篇文章【3】所说，其中包含了大量的bias。因此，那么怎样的图结构才算好叻？【3】说要没有偏见，随机才好。

顺便说一下，我个人觉得。NAS到这里应该自然知道什么是还可以做的。目前，whole network的搜索变成了local block的搜索。那么，显然通过如上的方式，将层数变连续是一个方向可以做，有人也做过。如果研究过DARTS你会发现还有几个超参： 网络的channel数（有人也做了），节点数以及其对应的连接线。那么显然也需要一个自动的版本。因此，【3】做的这个事情并不是想不到的。但是文章写法上，讲故事上真心赞。当然选用了Random Graph起码我是想不到的，顶多把node数也给连续了。

 

说回来，【3】这篇文章，将重点放在了网络的graph建模上。和DARTS不同，他们固定住其中的操作子（他们称作是transformation），很巧妙的引入了random graph，来搜索一个block当中应该有的连接方式。

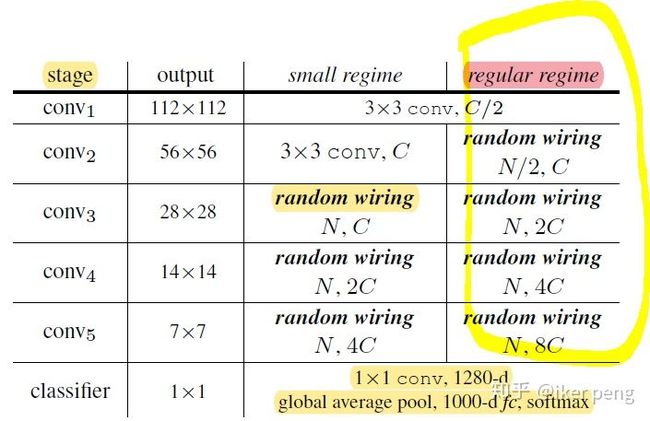
如图所示，作者构建了一个包含有5个blocks（他们称作是stage，其中两种配置分别针对mobile设计以及一般Network的设计），每一个block都通过一个随机graph来建模。这个工作当中采用了三种 Random Graph。分别是ER， BA和WS。 ER就是对任意两个Node之间以一定的概率连接； BA初始化M个，然后逐一增加Node 直到N个（以一定概率连接M个）。这里重点说下WS，因为在文章说其取得的性能最好。

 

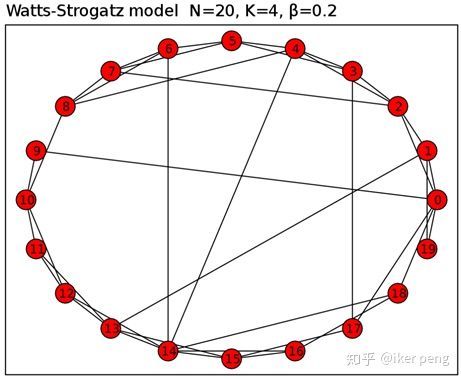
WS model属于一种small-world networks ，现实世界当中的social network，gene network都是这种。其最大的特点是： Small average distance, High clustering

拿来唬人的

如图所示就是一个WS graph。那么如何构造一个WS random graph呢？ 很简单。

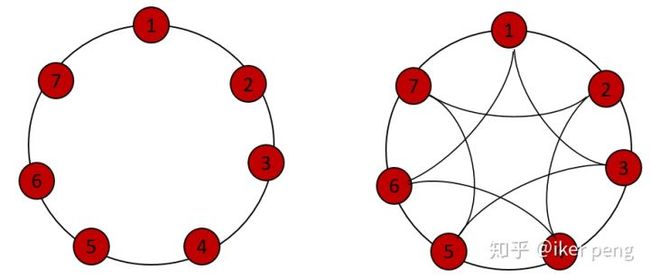
首先，WS随机graph会将图的节点放到一个环当中（ring）。来看两个正常（regular）的图：这里我们假设N=7，对于K=2，以及K=4的两种情况（K表示degree，是指每一个node周围的节点数目）图是这样的：

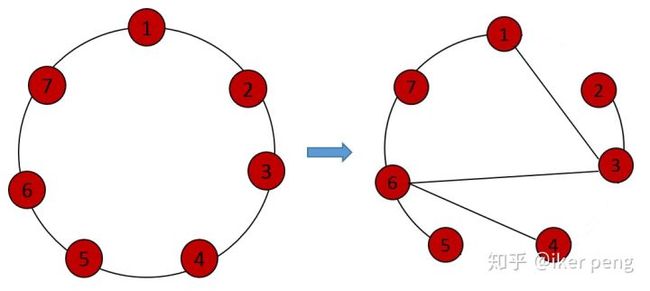
然后，在以上的基础上图当中的每一条边都以概率\beta 进行重新连接（rewiring）。也就是说原来的每一条边 以此概率断开，然后和它之后（顺时针）的某个节点随机的连接。这样便形成了WS 随机graph。我们以如上的K=2的regular的graph为例子，假设\beta =0.2, 那么构成的这个随机graph可能为如下的情况：

 

这里随机的断开了三条连接线，然后随机的和之后的节点进行连接。【3】当中所设计的网络就是在上图（右侧）的结构上设计的。

当我们得到如上的网络结构的时候，还存在一个待解决的问题，那就是哪些节点可以作为输入的节点，哪些又是输出的节点呢？ 由于我们对网络当中的节点进行了编号，同时在随机断开edges，进行rewirig的时候是顺时针和该节点之后的节点进行的。 因此， 对于每一个节点，统计其相邻的节点，如果其所有邻节点的编号都大于当前节点的标号，那么我们认为当前节点为输入节点（input_node），反之，如果所有的邻节点的标号都小于当前的节点，那么我们认为当前的节点为输出节点（output__node）。其余的为中间节点。 逐一对于每一个输入节点，其上的操作子（transformation）对输入的feature map 都进行了resolution减半的操作（单边上，总体减少4倍）。

以下代码（代码参考 

@任家敏

 ）：将node进行分类：通过找到node的邻节点的方式来确定节点的类别，因为这里有一个size要统一的问题，因此分为： input_node 表示接受上一个stage输出的节点，输入的feature maps resolution要减半（stride=2），其余节点都保持分辨率。 output_node 将所有从其而来的结果element-wise相加然后求平均作为该stage的输出。

def get_graph_info(graph):
  input_nodes = []
  output_nodes = []
  Nodes = []
  for node in range(graph.number_of_nodes()):
    tmp = list(graph.neighbors(node))
    tmp.sort()
    type = -1
    if node < tmp[0]:
      input_nodes.append(node)
      type = 0
    if node > tmp[-1]:
      output_nodes.append(node)
      type = 1
    Nodes.append(Node(node, [n for n in tmp if n < node], type))
  return Nodes, input_nodes, output_nodes

而具体对于WS graph可以调用networkx 实现。对于每一个stage：

class StageBlock(nn.Module):
  def __init__(self, graph, inplanes, outplanes):
    super(StageBlock, self).__init__()
    self.nodes, self.input_nodes, self.output_nodes = get_graph_info(graph)
    self.nodeop  = nn.ModuleList()
    for node in self.nodes:
      self.nodeop.append(Node_OP(node, inplanes, outplanes))

  def forward(self, x):
    results = {}
    for id in self.input_nodes:
      results[id] = self.nodeop[id](x)
    for id, node in enumerate(self.nodes):
      if id not in self.input_nodes:
        results[id] = self.nodeop[id](*[results[_id] for _id in node.inputs])
    result = results[self.output_nodes[0]]
    for idx, id in enumerate(self.output_nodes):
      if idx > 0:
        result = result + results[id]
    result = result / len(self.output_nodes)
    return result

其中表示的是，首先找出input_nodes 接收上一stage的输出，得到的输出，作为当前其他节点的输入；然后，对于其余的节点，以input_nodes的输出为输入计算各自的输出。最后，找出标记为output_node的节点，作为当该stage的输出。

 

【1】Zoph, Barret, and Quoc V. Le. "Neural architecture search with reinforcement learning."arXiv preprint arXiv:1611.01578(2016).

【2】Liu, Hanxiao and Simonyan, Karen and Yang, Yiming. DARTS: Differentiable Architecture Search.

【3】Xie, S., Kirillov, A., Girshick, R. and He, K., 2019. Exploring Randomly Wired Neural Networks for Image Recognition.arXiv preprint arXiv:1904.01569.