基于随机游走Random Walk的图节点Node表示
前言
在图中,如果能把节点表示成合适的数值,能做很多任务,例如节点分类,关系预测,聚类等等。如何把节点表示成计算机能看懂的数值目前也有很多方法,本文主要为大家介绍基于Random Walk的节点表示方法。
Embedding Nodes
既然要对node进行embedding,那么我们可以参考下word embedding,在nlp中,embedding过后的同意词,通常会聚在一起,
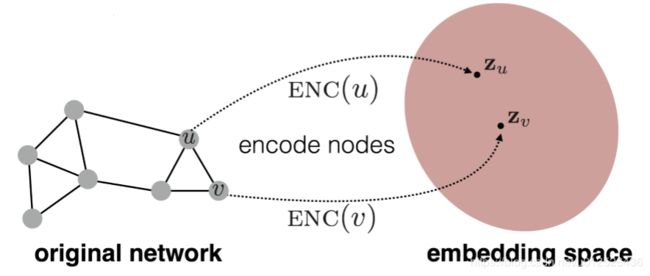
同样的,如果我们对图的节点进行embedding,有关系的节点,我们自然希望其embedding之后能聚在一起,如下图所示
也就是说,我们希望embedding之后的node vector点乘之后的值(可以理解为未归一化的cosine)接近于原graph中的节点相似度,原图的相似度可以采用是否节点相连,是否有相同的邻居节点等方式来定义。
s i m i l a r i t y ( u , v ) = z v T z u similarity(u,v)=z_v^Tz_u similarity(u,v)=zvTzu
根据上面的内容,我们为生成node embedding定义三个步骤
- 定义生成embedding的encoder
- 定义一个节点相似度的计算函数
- 优化encoder的参数,让其点乘后的结果约等于相似度
一种简单的Embedding方法
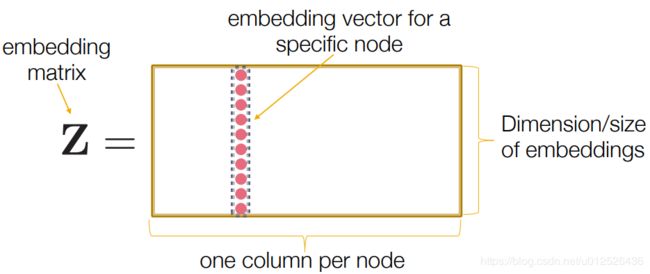
采用类型word embdding的方式,定义一个embdding lookup矩阵
e n c o d e r ( v ) = Z v encoder(v)=Zv encoder(v)=Zv
其中Z是嵌入矩阵,v是节点的one-hot表示方式
这样每个节点就能对应唯一的一个embedding vector。
接下来我们考虑第二步,怎么来定义我们上面提到的原图的相似度呢,判断节点是否有关系?是否有相同的邻居节点?显然,这些都不是很好的方式,并且没法进行度量。
Random Walk
随机游走是指给定一个图和一个起始节点,随机选择一个邻居节点,走到该处后再随机选择一个邻居,重复length次。length是指随机游走的长度。
使用随机游走从起始节点到终止节点的概率值,实际上就可以用来表示相似度,也就是说,从u节点到v节点的概率值,应该正比于u节点与v节点embedding之后的点乘结果。
z v T z u ∝ P ( v ∣ u ) z_v^Tz_u \propto P(v|u) zvTzu∝P(v∣u)
这种方法有两个优点
- 相似度的定义结合了局部信息与高阶领域信息。
- 只需要考虑随机游走的节点,不需要考虑全局信息,效率高。
参数优化
接下来是第三步,参数优化,给定图 G = ( V , E ) G=(V,E) G=(V,E),定义 N R ( u ) N_R(u) NR(u)表示采用策略R得到的邻居节点,我们的目标就是学习映射关系z
z : u → R d z:u\rarr \Bbb{R}^d z:u→Rd
表示为对数似然函数为
m a x ∑ u ∈ V l o g P ( N R ( u ) ∣ z u ) max \sum_{u \in V} log P(N_R(u) | z_u) maxu∈V∑logP(NR(u)∣zu)
简单解释下,即我们希望给定 u u u的embedidng z u z_u zu,我们希望其邻居节点出现的概率最大。最终损失函数可以表示为:
L = − ∑ u ∈ V ∑ v ∈ N R ( u ) l o g ( P ( v ∣ z u ) ) L = -\sum_{u\in V} \sum_{v \in N_R(u)} log(P(v|z_u)) L=−u∈V∑v∈NR(u)∑log(P(v∣zu))
P ( v ∣ z u ) = e x p ( z u T z v ) ∑ n ∈ V e x p ( z u T z n ) P(v|z_u) = \frac{exp(z_u^Tz_v)}{\sum_{n \in V} exp(z_u^Tz_n)} P(v∣zu)=∑n∈Vexp(zuTzn)exp(zuTzv)
注意softmax的分母z的下标是n,我们只想让u的邻居出现概率最大。
到了这一步,我们就可以采用SGD等方法来优化参数了。但是,如果你仔细看损失函数,可以发现L的计算复杂度是很高的,因为其外面嵌套了两层的求和,因此时间复杂度是 ∣ V ∣ 2 |V|^2 ∣V∣2,有什么方法能降低其复杂度吗?
负采样
在计算分母的时候,上面的方面会针对有所有的几点进行一遍计算,为了简化该过程,使用类似word2vec中的负采样,只采样k个负样本
l o g ( e x p ( z v T z u ) ∑ u ∈ V e x p ( z v T z n ) ) = l o g ( σ ( z v T z u ) ) − ∑ i = 1 k l o g ( σ ( z v T z n i ) ) log(\frac{exp(z_v^Tz_u)}{\sum_{u\in V}exp(z_v^Tz_n)}) = log( \sigma(z_v^Tz_u))-\sum_{i=1}^klog(\sigma(z_v^Tz_{n_i})) log(∑u∈Vexp(zvTzn)exp(zvTzu))=log(σ(zvTzu))−i=1∑klog(σ(zvTzni))
k是一个超参数,k越高表示负样本的偏见越高,较高的K能得到更可靠的估计结果,通常k取5-20。
Node2Vec
random walk的每一步都是无偏游走,也就是说走到下一个邻居节点的概率都相同的,那么游走的结果可能会只关注局部信息类似BFS(甚至是两个节点来回跳),或者只关注全局信息类似DFS,如下图所示。
N B F S ( u ) = s 1 , s 2 , s 3 N_{BFS}(u)={s_1,s_2,s_3} NBFS(u)=s1,s2,s3
N D F S ( u ) = s 4 , s 5 , s 6 N_{DFS}(u)={s_4,s_5,s_6} NDFS(u)=s4,s5,s6
那么有没有什么方法能控制其游走的策略呢?node2vec提出了一种游走的策略,该策略包含两个参数
- p p用来控制返回上一个节点
- q q用来控制远离上一个节点,改参数也可以理解为采用dfs还是bfs的一个比例值
看个具体的例子
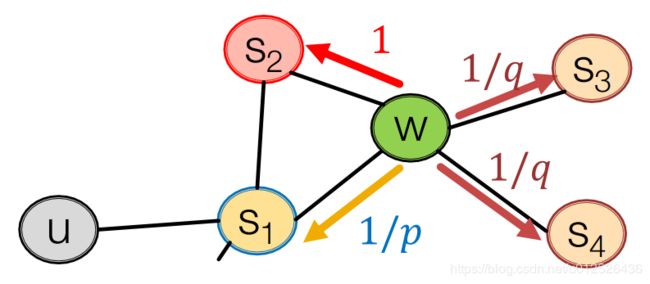
首先我们穿过了边(S1,W)走到了节点W,下一步该怎么走呢,此时,不同的路径会对应不同的概率值
- 如果是返回原节点,则概率为1/p
- 如果是原理原节点,则概率为1/q
- 如果和原节点具体保持不变,则概率为1
注意,这里的概率是一个非归一化的概率值
显然,如果我们想采用BFS,那么只需要调低p的值,如果想采取DFS,只需要调低q的值。这样游走的过程中,我们就可以自由的控制是想得到更多的局部信息还是全局信息。
最后总结一下node2vec的算法流程
- 定义随机游走的概率值
- 从节点 u u u开始,随机游走 l l l步
- 定义node2vec的的损失函数,并采用SGD进行参数优化
References
cs224w 7. Graph Representation Learning