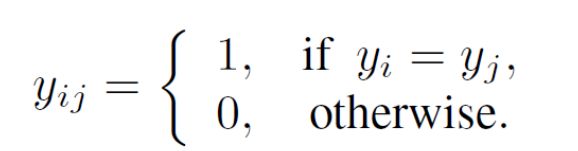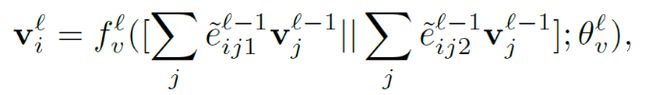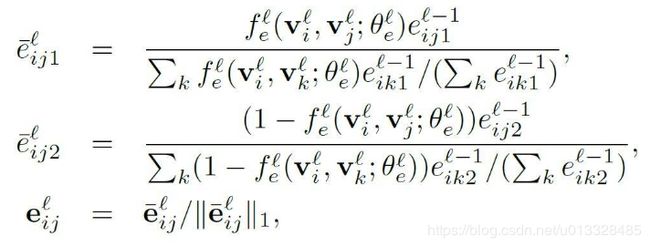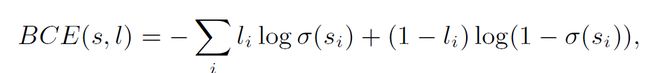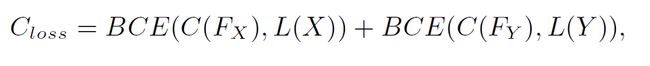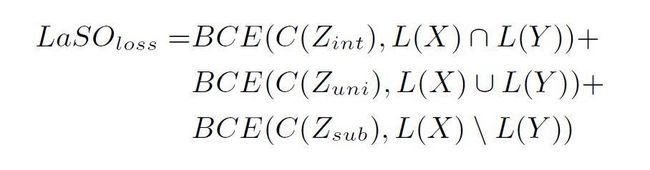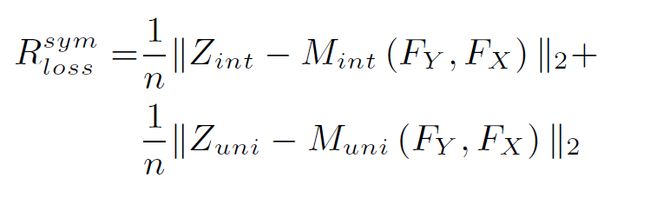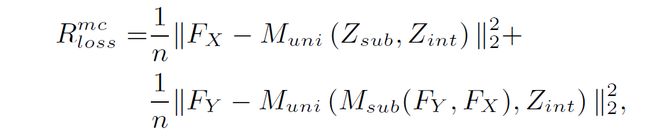CVPR2019 少样本学习
分类任务上的少样本学习
1.Edge-Labeling Graph Neural Network for Few-shot Learning(classification)
-
paper: https://arxiv.org/abs/1905.01436
-
code: https://github.com/khy0809/fewshot-egnn
-
图网络(Graph Neural Network, GNN)由于节点与节点之间具有相关性可以实现更丰富的信息传递,在近期来涉及到的推理问题(Reasoning)或者是视觉问答(Visual Question Answering)等任务上都有不少的尝试,而少样本学习(few-shot learning)的难点通常是在于可用样本有限,所以样本之间潜在的关联性在学习过程中就变得非常重要了,通用的前馈网络很难捕捉到样本之间丰富的关联信息,图网络正好可以弥补这一点:图网络在节点之间构建的丰富的连接,使得其能够利用节点之间的信息传递机制得到邻节点的信息并且进行聚合,通过一定复杂程度的图网络,就能够表达数据个体之间丰富的关联互动特征。
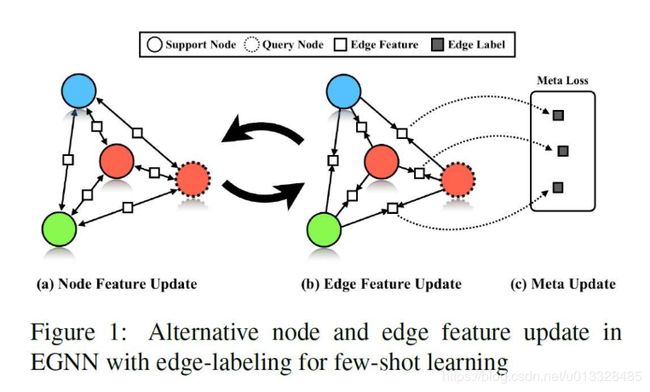
常见的图网络关注于节点的表示与特征嵌入,为了更充分的利用节点的关联信息,本篇论文提出了边标记图网络(Edge-Labeling Graph Neural Network,EGNN),类比于关注节点信息的 GNN,EGNN 通过迭代更新连接边的信息直接可以反映节点之间的类内相似度(intra-cluster similarity)与类间差异度(inter-cluster dissimilarity)从而获取正确的类别分配结果。另一方面,EGNN 在无需 re-train 的情况下能很好地适应不同数目的类别,并且很容易扩展到转换式推理(Transductive Inference)上面,同时在现有的 GNN 方法中,EGNN 在分类任务上实现了大幅的性能提升。
-
在图中首先更新节点特征,之后再更新节点之间连接边的特征,因为一组节点的特征有变化,进而也会影响到连接边上的特征,以及衡量节点之间的类内相似度(intra-cluster similarity)与类间差异度(inter-cluster dissimilarity)的参数也会对应得到更新,在边和点的特征都得到更新之后,计算边损失(Edge Loss),用 episodic training 的训练策略来更新 EGNN 的权重。
-
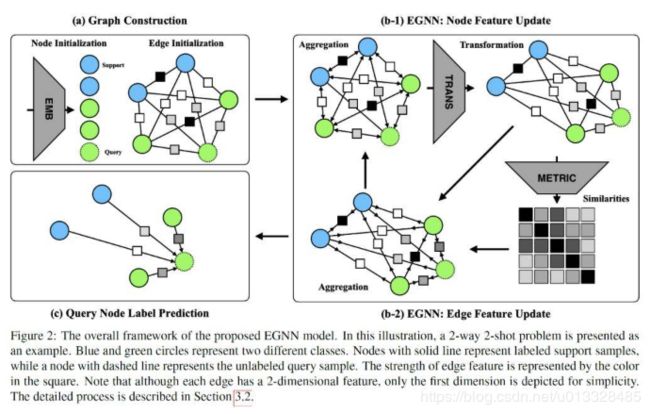
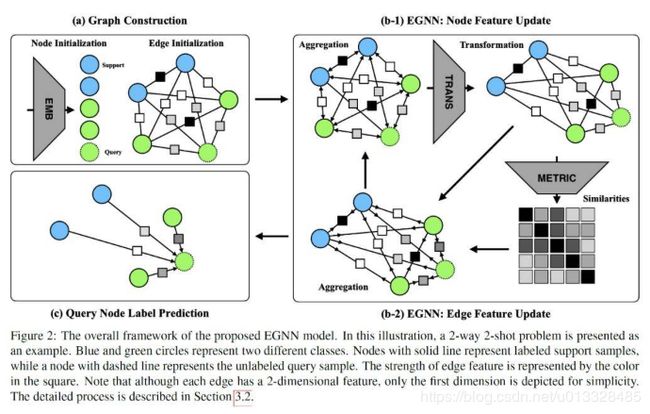
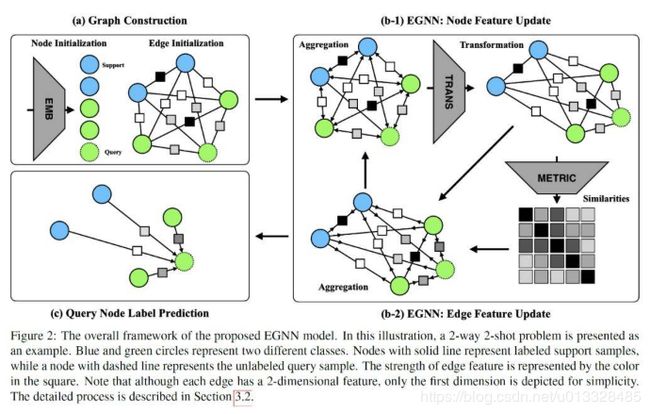
接下来我们会从少样本分类学习的问题定义入手,结合一个二分类的例子来阐述 EGNN 的各个模块与更新算法规则,帮助我们理解 EGNN,最后顺延扩展到论文实验中真正部署的多分类任务。少样本分类顾名思义就是通过每个类别极少或较少的训练样本来学习泛化而且鲁棒的分类器能够保持较高的准确度并且具有扩展性从而识别新的类别。由此,每个分类的任务 T(Task)都包含一个支持集 S(Support Set)与查询集 Q(Query Set),支持集是一个已包含标签的数据集,查询集则是未经标记的数据集,也正是学好的分类器进行验证的一个数据集。如果支持集 S 包含 N 个类,每个类别对应有 K 个标记数据,那么我们称此类问题为 N 路 K 样本分类问题(N-way K-shot classification problem),现在我们假设手上有两个类别的数据,支持集 S 中每个类别有两个样本,查询集 Q 有一个未标记样本(类似测试样本,我们已知标签,但是对于网络并不透露它)我们将这个问题归为 2 类 2 样本问题,参考下图 EGNN 框架图,我们一个模块一个模块来理解推导:
-
a)我们将图像输入到卷积神经网络(Convolutional Neural Networks)中提取特征,得到数据样本的特征表示,之后根据已有特征建立邻接边并初始化,形成一张全连接图(fully-connected graph),每一条边都指代着它连接的两个节点的关系类型。图的构造用数学形式表示为 G=(V,E;T),对于每一个任务 T,一个图对应着一个节点集合 V,一个边集合 E。对于支持集的边标签我们采用节点的标签进行表示如下:
-
至于边的特征 e 我们一个数值范围在 [0,1] 区间内的二维向量来分别表示该条边连接的两个节点类内相似度(intra-cluster similarity)与类间差异度(inter-cluster dissimilarity),图网络同样也是多层网络,每层均可以按照类似的规则进行初始化。
-
b)图初始化完成之后,我们就根据之前提到过的信息更新流程,首先更新节点特征:
-
之后就是根据变换后的节点信息来更新边的特征:
-
c)在数次的节点、连接边特征迭代更新之后,我们可以从最近更新的边特征上得到最终的节点类别预测,用非常直接的加权投票(weighted voting)方法,结合支持集 S 里的样本标签以及它们与查询样本连接边的预测值,我们就可以很容易的推出待查询样本的所属类别,节点的预测概率可以表达为:
-
同样地,EGNN 的推理过程算法正如上述各个模块流程所述,详细的网络模块图与算法流程图如下:
-
综合看下来这篇文章在构思和实现方面都非常有创新,充分利用了图结构学习节点关联的特性,实验结果也非常有说服力,是非常有亮点的一个作品,也对之后图网络相关的工作提供了更多的启发。
2. LaSO: Label-Set Operations networks for multi-label few-shot learning (classification, multi-label)
paper: https://arxiv.org/abs/1902.09811
数学中集合运算的基本概念:集合的并(Union),交(Intersection),补(Complement)三大运算对于我们都不陌生。但是今天这篇论文提出,小样本学习(few-shot learning)情况下的图像多标签分类(multi-label classification)也能够实现类似集合一样的交,并,补操作。
对于小样本学习来说,核心难点经常是可用训练样本数目不足,解决的方法也多是寻求各种形式的样本合成(Example Synthesis),当然样本合成基本都是针对于单标签的普通分类情况,LaSO(Label Set Operation networks)在此基础上,提出了一个应用于多标签小样本分类场景下的样本合成方法,将一组图片输入到 LaSO 网络里,获取两张图片各自的特征,并将他们结合起来,学习在特征空间上的并集特征(union feature),交集特征(intersection feature)以及补集特征(compelemt feature)表示,这三个学习到的特征也会对应我们在多分类上的语义标签的并,交,补操作。
举例子来说明:我们希望训练一个野外各种类动物的分类器,然而目前我们手上仅有的却都是少量的关在笼子里的动物样本图片,笼中动物显然无法很好地泛化和学习到野外动物的特征表示,所以在 LaSO 提出的场景下,我们先将一张笼中公鸡与一张笼中兔的图片配位一对输入到网络中,让 LaSO 不只是学习到兔和公鸡的特征,同时还有我们完全没有涉及的笼子的特征,而笼子的特征恰好是两张输入图片的交集(intersection),我们取出这样的交集特征,同时再次输入一只笼中老虎的照片获得笼中虎特征,此时对笼中虎特征求它与笼子特征的补集(complement),我们从一定程度上就获得了「无笼子」的野生老虎的特征了,示意图如下:
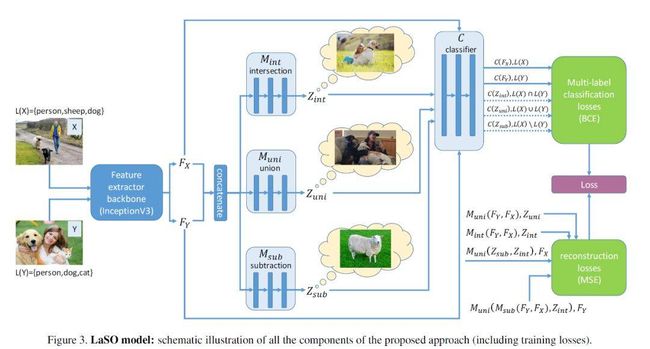
接下来我们一起看看 LaSO 的整个模型结构:
LaSO 模型接受一对图片 X,Y 为输入,分别进入骨干网络 B(文章采用 InceptionV3 以及 Resnet 作为特征提取网络)进行特征提取得到特征 Fx,Fy。在对两张图片的特征进行连接之后,根据我们希望学到的图像中个体类别的交,并,补,所以连接好的特征分别进入 LaSO 的交、并、补网络模块 Mint,Muni,Msub 中学习合成对应的特征 Zint,Zuni,Zsub,特征 Z 可以认为是对应着一张假设的图像 I,这张图像 I 中的个体类别恰好对应着输入 X,Y 的标签的并/交/补,举例说明 Zint 可以看做假设图 I 的提取特征,而图 I 的标签 L(I)正是输入 X 与 Y 的标签交集。
在这之后结合我们已经渠道的所有特征,训练一个分类器 C 并使用交叉熵损失函数(Binary Cross-Entropy Loss, BCE)来学习这个多标签分类的问题,同时之前学习合成特征 Z 的三个 LaSO 模块也采用一样的损失函数进行参数更新,具体表达式如下:
交叉熵损失函数:
分类器 C 损失函数:
LaSO 模块损失函数:
除此之外考虑到操作对称因素以及模型稳定因素,基于重构的均方误差(Mean Square Error,MSE)也作为另一部分的损失加载到模型的最后:
模型稳定损失:
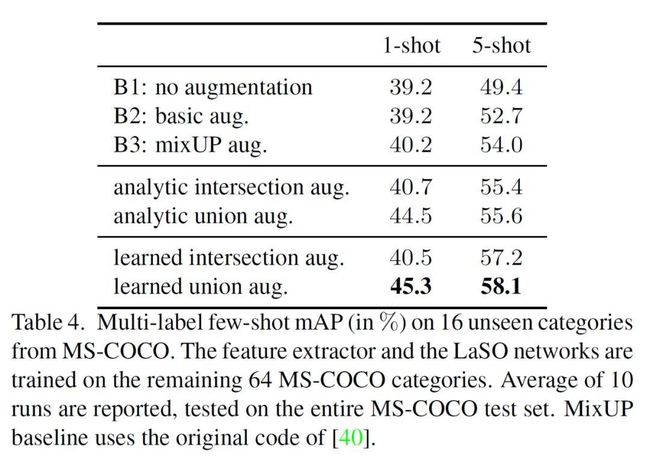
在实验过程部分,论文主要采用了 MS-COCO 2014 与 celebA 的数据集来进行实验和对比分析,将 COCO 数据集的 80 的物体类别随机分成 64 个已知类别与 16 个未知类别,并且使用平均精度(mean Average Precision,mAP)来衡量 LaSO 模块的学习能力,结果具体如下:
综合看来,这篇 LaSO 论文选题的角度非常有创新性,少量样本来学习多标签分类,并且使用集合中并、补、交的数学概念来操作图像标签,进行样本增广,反过来又辅助了少样本学习情况下样本缺乏的问题,提出的网络架构也非常直观易懂,虽然目前看来分类效果还有待提升,同时网络的训练目前也还是分批来进行,扩展的实验也没有那么丰富,但是它提出的新颖角度和方法,也仍然是值得关注的,相信之后也会有更多的思考和新的工作会更新,根据原文,LaSO 的代码也即将在近期公布供读者参考验证。
CVPR 其他少样本学习/无监督学习论文列表
注:加粗文章为 oral 文章, 未加粗文章是 poster
1.Generating Classification Weights with Graph Neural Networks for Few-Shot Learning(Oral)
2.Gradient Matching Generative Networks for Zero-Shot Learning(Oral)
-
paper:http://openaccess.thecvf.com/content_CVPR_2019/html/Huang_Generative_Dual_Adversarial_Network_for_Generalized_Zero-Shot_Learning_CVPR_2019_paper.html
3.Learning Inter-pixel Relations for Weakly Supervised Instance Segmentation(Oral)
-
paper:https://arxiv.org/abs/1904.05044
4.Unsupervised Person Image Generation with Semantic Parsing Transformation
-
paper:https://arxiv.org/abs/1904.03379
5.Rethinking Knowledge Graph Propagation for Zero-Shot Learning(Oral)
-
paper:https://arxiv.org/abs/1805.11724
6.Meta-Transfer Learning for Few-Shot Learning(Poster)
-
paper:https://arxiv.org/abs/1812.02391
7.Generative Dual Adversarial Network for Generalized Zero-shot Learning(Poster)
-
paper:https://arxiv.org/abs/1811.04857
8.Hierarchical Disentanglement of Discriminative Latent Features for Zero-shot Learning(Poster)
-
paper:https://arxiv.org/abs/1803.06731
9.Marginalized Latent Semantic Encoder for Zero-Shot Learning(Poster)
10.Spot and Learn: A Maximum-Entropy Image Patch Sampler for Few-Shot Classification(Poster)
11.Large-Scale Few-Shot Learning: Knowledge Transfer with Class Hierarchy(Poster)
12.Generalized Zero- and Few-Shot Learning via Aligned Variational Autoencoders(Poster)
-
paper:https://arxiv.org/abs/1812.01784
13.Dense Classification and Implanting for Few-shot Learning(Poster)
-
paper:https://arxiv.org/abs/1903.05050
14.On zero-shot recognition of generic objects(Poster)
-
paper:https://arxiv.org/abs/1904.04957
15.out-of-distribution detection for generalized zero-shot action recognition(Poster)
-
paper:https://arxiv.org/abs/1904.08703