Regularized Logistic Regression(Octave转换为Python)
详细代码参考github
Regularized Logistic Regression
实例：
建立Regularized Logistic Regression模型，预测微型集成芯片能否通过质量保证（QA）。我们有芯片两次不同的测试结果，要通过建立的模型预测处理器是否能够通过QA。
1.可视化数据
数据为118组芯片两次测试情况以及测试的结果，维度为（118，3），结果为1，通过，用“+”表示，否则不通过， 用“·”表示，从图中可以看出，无法用一条直线将两种结果区分开来，普通的逻辑回归无法解决该问题。
参考代码：
def plotData(self):
y1_index = np.where(self.y == 1.0)
x1 = self.x[y1_index[0]]
y0_index = np.where(self.y == 0.0)
x0 = self.x[y0_index[0]]
plt.scatter(x1[:, 0], x1[:, 1], marker='+', color='k')
plt.scatter(x0[:, 0], x0[:, 1], color='y')
plt.legend(['y = 1', 'y = 0'])
plt.xlabel('Microchip Test 1')
plt.ylabel('Microchip Test 2')
# plt.show()
2.Feature mapping
通过数据分布，单纯的一条直线解决不了问题，我们尝试用两种测试结果的多项式形式来处理，最高6次幂，这样边界将是一条曲线，如果多项式的最高次幂太高的话，容易过拟合，太低的话容易欠拟合，通过mapFeature函数，将2组特征数据，转换为28组特征数据，其中第一组数据是1，其余数据按照下式生成。
参考代码：
def mapFeature(self, x1, x2):
# 生成多项式
out = np.ones((x1.shape[0], 1))
for i in range(6):
for j in range(i+2):
out = np.hstack([out, (x1**(i+1-j)*(x2**j))])
return out
3.损失函数和梯度
同普通的逻辑回归一样，只不过多了一部分正则化项，公式如下，容易忽略的地方，参数theta0是不需要正则化的，故下标是从1开始。
损失函数的梯度公式，分为两部分，同样theta0不需要正则化。
参考代码：
def costFunctionReg(self, theta, lanmda):
m = self.y.shape[0]
J = (-np.dot(self.y.T, np.log(self.sigmoid(self.map_x.dot(theta))))-np.dot((1-self.y).T, np.log(1-self.sigmoid(self.map_x.dot(theta))))) / m+ (lanmda*np.sum(theta[1::]**2, axis=0))/(2*m) # 正则化从j = 1开始
return J
def gradient(self, theta, lanmd):
m = self.y.shape[0]
theta = theta.reshape((self.map_x.shape[1], 1))
grad = np.zeros((self.map_x.shape[1], 1))
grad[0] = np.dot(self.map_x[:, 0:1].T, (self.sigmoid(self.map_x.dot(theta))-self.y)) / m
grad[1::] = np.dot(self.map_x[:, 1::].T, (self.sigmoid(self.map_x.dot(theta))-self.y)) / m + lanmd*theta[1::] / m
# grad = np.dot(self.map_x.T, (self.sigmoid(self.map_x.dot(theta)) - self.y)) / m
return grad
4.求解最优的theta
同样使用scipy.optimize中的minimize函数，注意参数的数量，在梯度和损失函数定义的两个函数中，传入参数为2个，故minimize函数使用args=()参数。
参考代码：
def fminunc(self): # costFunction需要几个参数就传几个,本例有两个,x0,利用args=(100, )
optiTheta = op.minimize(fun=self.costFunctionReg, x0=np.zeros((28, )), args=(100, ), method='TNC', jac=self.gradient)
return optiTheta # dict
这里出现一个问题：当设置lambda值为0.1、1、10、100时均可求出最优theta，但当lambda=0时，始终返回failure，找不到最优解，有大神看到还请帮忙解答。
5.绘制决策边界
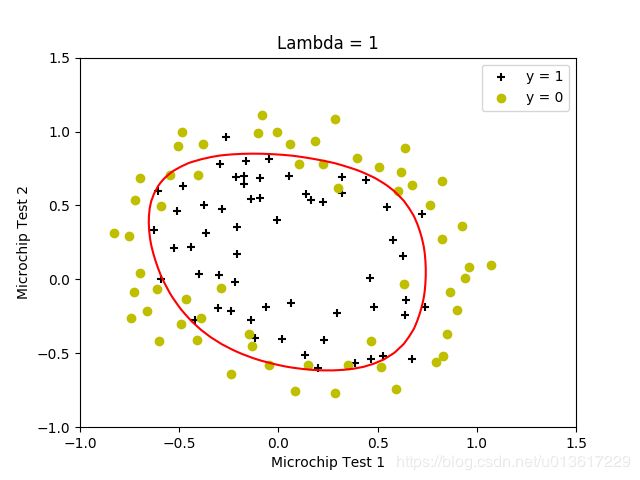
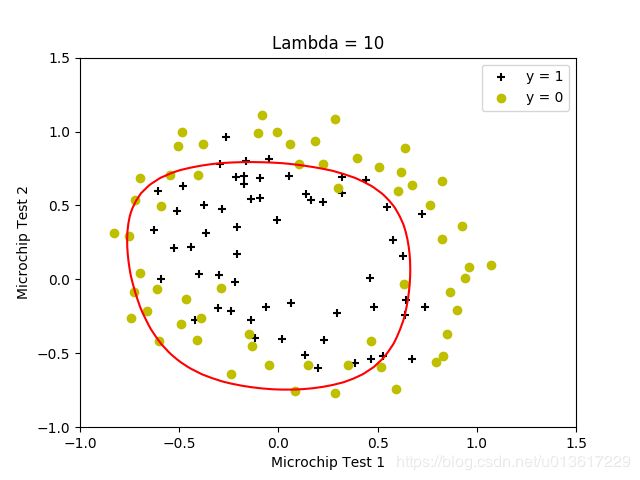
按照设置的lambda值，生成了四个结果。原试验中还有lambda=0的情况，但上面求解函数中求不到值，把原octave试验结果贴出来，放在一起便于分析。
清楚的看出来，当lambda较小的时候，边界可以将训练数据很好的分开，但是边界非常复杂，明显的过拟合；当lamda=100的时候，得到了偏移很多的决策边界，没能很好的区分，欠拟合，找到较为的合适的lambda值，是求得较好结果的关键。
5.lambda值
贴出吴老师用手注灵魂的PPT，当lambda很大很大的时候，要最小化J，所有的theta就会很小很小，约等于0，那么求出来的h(theta)函数就近似一条直线，结果欠拟合；lambda很小的时候，正则化项几乎不起作用，不能很好的处理过拟合。
