数据结构与算法：B树（B-Tree）定义及搜索、插入、删除基本操作

版权声明：本文为博主原创文章，转载请注明出处，https://blog.csdn.net/u014165620/article/details/82976882

B树（B-Tree）

在介绍什么是B树（B-Tree）之前，先看看为什么存在B树结构？
B树（B-Tree）是为磁盘或者其他辅助存储设备而设计的一种平衡搜索树，如有的数据库系统使用B树或者B树的变种来存储信息。B树的节点可以有很多孩子，从数个到数千个，不同于一般的二叉树（每个节点最多只有两个孩子）。

下面以磁盘为例说明B树的设计目的。下图是一个典型的磁盘驱动器：

磁盘通过盘片的旋转以及磁臂的移动定位然后读/写数据。目前，商用磁盘的旋转速度是5400~15000转/分钟(RPM)，以7200RPM为例，盘片旋转一圈需要8.33ms，比内存的常见存取时间50ns要高出5个数量级，同时磁臂移动也需要时间，所以即使按平均只需要等待半圈计算，磁盘存取时间与内存存取时间的差距仍是巨大的。因此，为提高应用效率，提高数据处理速度，需要尽可能降低磁盘存储次数。在一棵树中检查任意一个节点都需要一次磁盘访问，因此B树的设计避免了大量的磁盘访问。

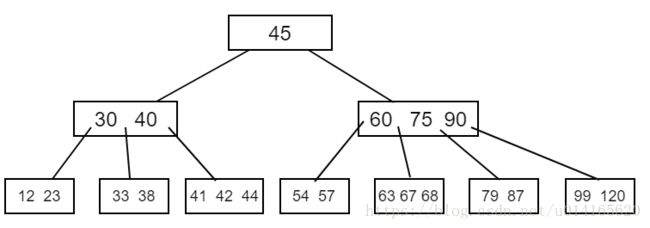
B树的定义

一棵B树（B-Tree）是有如下性质的树：

1. 每个节点 x 有下面属相：
   a. x.n，节点 x 中的关键字个数；
   b. n个关键字 x.key1, x.key2, x.key3, … , x.keyn 以非降序排序，即 x.key1 <= x.key2 <= x.key3 <= … <= x.keyn ;
   c. x.leaf，一个布尔值，表示 x 是否为叶结点，是则为True，否则为False。
2. 每个内部节点 x 最多包含 x.n + 1 个孩子（类似一条直线上n个点将直线分成 n+1 段），x.c(i) 为指向其第i个孩子的指针，叶结点没有孩子，所以叶结点的x.c(i)没有定义。
3. 关键字x.key(i) 对存储在各子树中的关键字范围加以分割（同样的，类似直线上的点将直线分段）：如果 k(i) 为 x.c(i) 对应的的子树中的关键字，则：
   k1 <= x.key1 <= k2 <= x.key2 <= … <= x.keyn <= k(n+1)
   即，对于节点关键字x.key，左边子树的关键字不大于key，右边子树的关键字不小于key。
4. 每个叶结点具有相同的深度，即树的高度h。
5. 每个叶结点包含的关键字个数有上界和下界。用一个被称为B树的最小度数（minmum degree）的固定整数 t >= 2 来表示这个界：
   a. 除根节点以外的每个内部节点至少有 t 个孩子，除根节点以外的每个结点至少有 t-1 个关键字。如果树非空，根结点至少有一个关键字。
   b. 每个内部结点最多有 2t 个孩子， 最多有 2t-1 个关键字。如果一个节点恰好有 2t-1 个关键字，则称该结点是满的（full）。

下面就是一棵B树：

B树的高度

B树上大部分操作所需磁盘存取次数与B树的高度成正比。对于B树的高度，有如下定理：
如果 n >= 1，那么对任意一棵包含n个关键字、高度为h、最小度数t >= 2 的B树T，有
所以，每个结点包含的关键字个数越多，B树的高度越小，从而磁盘存取次数越少。

B树上的基本操作

搜索B树

搜索一棵B树与搜索二叉查找树类似，只是在每个节点所做的不是二叉两路分支选择，而是根据结点的孩子数做多路分支选择。B树搜索伪代码如下：

B-Tree_Search(x, k)
	i = 1
	//找出最小下标 i ，使得 x.key[i] >= k
	while i <= x.n && x.key[i] < k                  
		i = i + 1
	//检查是否找到该关键字，找到则返回，否则后面结束此次查找
	if i <= x.n && k == x.key[i]
		return (x, i)
	else if x.leaf
		return null
	else DISK-READ(x, c[i])
		return B-Tree_Search(x.c[i], k)

B-Tree_Search(x, k) 的输入是一个指向某（子）树根结点x的指针，以及待搜索关键字k，返回结点 y 以及使得 y.key[i] == k 的下标 i 组成的有序对 (y, i) ，否则返回null。

插入关键字

向一棵与二叉查找树插入新结点一样，需要查找插入新关键字的叶结点的位置。如果待插入的关键字已经存在，则返回该关键字位置 (x, i)，不用再插入。与二叉查找树不同的是，B树的插入不能随便新建叶结点，否则会导致违反B树性质，所以在已有叶结点中插入。但是如果插入叶结点 y 是满的(full)，则需要按其中间关键字$y.ke{y}_t$将 y 分裂（split）两个各加粗样式含 t-1 个关键字的非满结点（满结点的关键字个数为 2t-1 ），中间关键字$y.ke{y}_t$被提升到 y 的父结点，以标识两棵新树的划分点。但是如果 y 的父结点也是满的，则其父结点也需要分裂，以此类推，最终满结点的分裂会沿着树向上传播。

上面过程可能需要一下一上两个操作过程：1.自上而下查找插入叶结点位置；2.自下而上分裂满结点。可以对该过程稍作修改，从树根到叶结点这个单程向下过程中将关键字插入B树中。为此，不是等到找出插入过程中实际要分裂的满结点时才做分裂，而是自上而下查找插入位置时，就分裂沿途遇到的每个满结点（包括叶结点），这样，当分裂一个满结点 y 时，可以保证它的父结点不是满的。

分裂一个 t = 4 的结点 x 示意图如下：

分裂结点伪代码如下：

//分裂x结点的第i个孩子
B-Tree-Split-Child(x, i)
	y = x.ci
	//分配新节点z
	z = ALLOCATE-NODE()
	z.leaf = y.leaf
	z.n = t - 1
	//使用y后半部分的关键字初始化z的关键字
	for j=1 to (t-1)
		z.key[j] = y.key[j+t]
	y.n = t - 1
	//将x中i后面的所有指向孩子的指针向后移一位
	for j=(x.n + 1) downto (i+1)
		x.c[j+1] = x.c[j]
	//x的第（i+1）个孩子为新结点z
	x.c[i+1] = z
	//将x中i后面的所有关键字向后移一位
	for j=x.n downto i
		x.key[j+1] = x.key[j]
	//将y的中间关键字y.key[t]向上提为父结点x的第i个关键字
	x.key[i] = y.key[t]
	x.n = x.n + 1
	//写磁盘
	DISK-WRITE(x)
	DISK-WRITE(y)
	DISK-WRITE(z)

插入伪代码如下：

//在B树T中插入关键字k
B-Tree-Insert(T, k)
	r = T.root
	//如果根结点r是满的，需要向上新提一个根结点
	if r.n == 2t - 1
		s = ALLOCATE-NODE()
		T.root = s
		s.leaf = False
		s.n = 0
		s.c[1] = r
		B-Tree-Split-Child(s, 1)
		//向以非满结点s为根的树中插入关键字k
		B-Tree-Insert-NonFull(s, k)
	else
		B-Tree-Insert-NonFull(r, k)

向以非满结点x为根的树中插入关键字k的伪代码如下：

//向以非满结点x为根的树中插入关键字k
B-Tree-Insert-NonFull(x, k)
	i = x.n
	//叶结点，直接在该结点插入
	if x.leaf
		while i >= 1 && k < x.key[i]
			x.key[i+1] = x.key[i]
			i = i - 1
		x.key[i+1] = k
		x.n = x.n + 1
		DISK-WRITE(x)
	//内部结点，需要找到插入的叶结点位置
	else
		while i >= 1 && k < x.key[i]
			i = i  - 1
		i = i + 1
		DISK-READ(x.c[i])
		if x.c[i].n == (2t-1)
			B-Tree-Split-Child(x, i)
			if k > x.key[i]
				i = i + 1
		B-Tree-Insert-NonFull(x.c[i], k)

删除关键字

B树上的删除操作与插入操作类似，但是略微复杂一点，因为可以从任意一个结点删除一个关键字，而不仅仅是叶结点，而且当从一个内部结点删除一个关键字时，还需要重新安排这个结点的孩子。与插入操作一样，必须防止因删除操作而导致树的结构违反B树性质。就像插入操作必须保证结点关键字不会因为插入新关键字而太多一样，删除操作也必须保证结点关键字不会因为删除关键字而太少（根结点除外，因为它允许关键字个数比最少关键字数 t-1 还少）。因此与插入需要分裂结点类似，当从一个只有最少关键字个数的非根结点中删除关键字后，需要从其父结点把一个关键字移到该子结点中，与分裂需要向上回溯一样，下降关键字到子结点的操作可能也需要回溯。

与插入类似，删除操作也可以在第一趟下降过程中，处理沿途遇到的所有关键字个数为最少关键字数（t-1）的结点（根节点除外），将其父结点的一个关键字下降到该子结点，而不是删除关键字后需要下降关键字时才从其父结点下降，这样可以保证下降关键字到子结点后，父结点的关键字数不会少于最少关键字数（t-1），因此不用向上回溯。

下面介绍删除操作如何工作，从B树中删除关键字分为以下几种情况：

1. 如果关键字 k 在结点 x 中，且 x 是叶结点，则直接从x中删除k即可；
2. 如果关键字 k 在结点 x 中，且 x 是内部结点，则做以下操作：
   a. 如果结点 x 中前于 k 的子节点 y 至少包含 t 个关键字，则找出 k 在以 y 为根的子树中的前驱 k’（子树中最“大”的关键字）。递归的删除 k’，并在 x 中用 k’ 代替 k 。
   b. 对称的，如果 y 有少于 t 个关键字（t-1个），则检查结点 x 中后于 k 的子结点 z，如果 z 至少有 t 个关键字，则找出 k 在以 z 为根的子树中的后继 k’（子树中最“小”的关键字）。递归的删除 k’，并在 x 中用 k’ 代替 k 。
   c. 否则，如果 y 和 z 都只含有（t-1）个关键字，则将k和z的全部合并进 y ，这样 x 就失去了 k 和指向 z 的指针，并且 y 现在包含（2t-1）个关键字。然后释放 z 并递归从 y 中删除 k 。

由于一棵B树中的大部分关键字都在叶结点中，所以在实际中，删除操作经常是从叶结点删除关键字。

最后，推荐一个B树的可视化网站，方便对B树的理解。

以上就是二叉树的介绍，如有不对的地方，感谢指正！

参考《算法导论》