机器学习４——推荐系统

整理自coursera,欢迎交流转载。

背景

　　现在我们考虑一个个性化的推荐系统，比如推荐电影、商品等。我们应该如何构建这个系统呢？其实推荐的方法有很多。比方说我们可以根据商品的流行度来推荐，这个方法最大的缺点是缺少个性化；为了实现个性化，我们可以把商品分类，根据分类来向用户推荐，这种方法的输入是用户的购买或浏览历史的特征，输出是用户可能喜欢的商品或多媒体信息，这个方法的优点是个性化、考虑到了具体情景、在用户信息比较少的时候也可以良好工作（比方知道用户年龄或者性别就可以来进行推荐），但是缺点是用户信息很少的时候无法正常工作。下面我们究其中一些方法结合亚马逊商品推荐来进行讲解。

协同过滤技术

　　以亚马逊购物为例，用户Ａ购买了尿不湿，我们怎么给Ａ推荐他可能感兴趣的商品呢？我们可以看看还有哪些用户购买了尿不湿，比方我们发现用户Ｂ和Ｃ都购买了尿不湿，并且Ｂ和Ｃ同时也够买了其他的商品，我们就可以认为Ａ也对这些其他商品感兴趣。我们找到同时购买尿不湿和其他商品的记录，做出如下向量：

项目	牛奶	婴儿奶嘴	婴儿玩具	洁厕灵
与尿不湿同时购买数量	12	127	50	5

　　如果我们把所有商品条目分别作为横纵坐标，就可以得到矩阵Ｃij，表示购买i的同时有购买j的人数，很明显Ｃij是一个对称方阵。

矩阵正规化

　　先看一个情景，比方我们有一种销量特别大的商品，比如尿不湿。由于每个购买婴儿用品的买家都很有可能会购买尿不湿。再来看另一种商品——一个婴幼儿玩具，比方我们刚刚购买了一个这种小玩具，那么我们极有可能会被推荐一起购买尿不湿。其实不管我们购买什么养的婴儿玩具，基于上面描述的Ｃ矩阵，我们几乎都会被推荐一起购买尿不湿。因此我们需要克服流行商品推荐力过强的问题。
　　　　　　　　　　
　　　　　　　　　　　　长颈鹿婴幼儿磨牙器

杰卡德相似系数(Jaccard similarity coefficient)

杰卡德相似系数定义

　　两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示。
　　　　　　
　　杰卡德相似系数是衡量两个集合的相似度一种指标。

杰卡德距离

　　杰卡德相似系数相反的概念是杰卡德距离(Jaccard distance)。杰卡德距离可用如下公式表示：
　　　　
　　杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。

杰卡德相似系数与杰卡德距离的应用

　　可将杰卡德相似系数用在衡量样本的相似度上。样本A与样本B是两个n维向量，而且所有维度的取值都是0或1。例如：A(0111)和B(1011)。我们将样本看成是一个集合，1表示集合包含该元素，0表示集合不包含该元素。

p ：样本A与B都是1的维度的个数
q ：样本A是1，样本B是0的维度的个数
r ：样本A是0，样本B是1的维度的个数
s ：样本A与B都是0的维度的个数

　　那么样本A与B的杰卡德相似系数可以表示为：
　　这里p+q+r可理解为A与B的并集的元素个数，而p是A与B的交集的元素个数。
　　而样本A与B的杰卡德距离表示为：
　　　　

进一步改进

　　即使做了上述处理，我们的模型仍然有很多缺陷，
因为我们知识考虑了用户当前正在购买的商品，而没有考虑用户的购买历史。作为一种改进的策略，我们可以作如下调整：
　　用户β正在购买物品Ａ，并且查询用户的购买记录，发现用户同时购买过Ｂ，Ｃ，Ｄ物品，现在我们们需要看看物品Ｅ对此用户的吸引力，可以如评分：
　　Score(β，Ｅ)=[S(A,B)+S(A,C)+S(A,D)]/3【S(A,C)表示同时购买过Ａ和Ｃ的人数】
　　这样调整以后我们就考虑到了购买历史的因素，但是即使如此我们依旧有很多因素没有考虑，比如购买时间，用户性别、年龄等。

一个简单的电影推荐系统

　　到目前我们所讨论的方法，都仅仅是根据购买量和用户购买历史的简单计算来推荐，因此我们很自然的会问，我们能否使用用户特征和产品特征的集合来驱动推荐，使得推荐更加个性化呢？下面我们就介绍一种这样的方法。并且这次课程，我们需要从数据中学习这些特征，而不是一开始就知道用户和电影的特征。

　　假设我们收集了一个用户观看的电影列表，就类似下面这样：

用 户	电 影	评 分(0~5)
小明	《地球四季》	4.9
小明	《爵迹》	０.9
小明	《星际迷航３》	4.5
小红	《爵迹》	2.9
小红	《火影忍者·博人传》	4.3
小红	《地球四季》	4.2
小刚	《星际迷航３》	4.9
小刚	《小时代４》	3.9
小方	《爵迹》	1.9
小方	《小时代４》	2.3

　　接下来我们用矩阵表示这个关系，每行代表一个用户，每一列代表一部电影如下：

内容	《地球四季》	《爵迹》	《星际迷航３》	《火影忍者·博人传》	《小时代４》
小明	4.9	0.9	4.5	?	?
小红	4.2	2.9	?	4.3	?
小刚	?	?	4.9	?	1.9
小方	?	1.9	?	?	2.3

　　我们用Ｕ表示用户，Ｖ表示电影，则上述矩阵可表示为Rating(u, v)，值得注意的是用户为看过的电影评分不是０，而是未知。由于每个用户只看过一小部分电影，每部电影也只有一部分用户观看，所以实际上Rating矩阵是一个稀疏矩阵。我们们需要做的就是根据我们观测道德部分数据来预测用户对没有看过的电影评分，找出此用户可能喜欢的（预测评分高的）电影推荐给这个用户。
　　那么具体该怎么做呢？我们怎么去填补Rating的“？”部分呢？假设我们已经知道了用户喜好和电影类型，比如用户喜好向量表示为：
　　Lu=[2.5 5 0.1 1.2 … … ](分别表示对动作片，科幻片，浪漫片，喜剧片……的喜爱程度）
　　电影类型向量：
　　Rv=[0.1; 0.5; 4.6; 1.2; … … ](分别表示对动作片，科幻片，浪漫片，喜剧片……的含量）
　　那么我们可以得到对于这部电影，此用户的预测评分可能为:
　　　dot(Lu, Rv)=2.5×0.1+5×0.5+0.1×4.6+1.2×1.2+… …　= 3.7
　　而另一部电影的预测评分为４．８，显然我们应该向该用户推荐后者。
　　把这个思想扩展到所有的用户和电影：
　　L=[Lu1; Lu2; Lu3, … …]
　　R=[Rv1, Rv2, Rv3, … …]
　　则,Rating(u, v) = L·R
　　
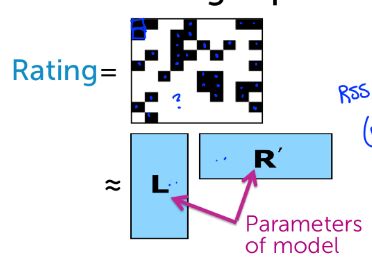
　　我们需要做的就是找到这些Ｌ和 R ，具体的矩阵分解方法不在这里具体描述，大致和回归思想差不多，找到预测得分和实际的分的方差和最小的Ｌ和Ｒ，然后我们就可以用Ｌ和Ｒ求得完整的Rating矩阵，对每名用户排序后可以得到最值得推荐的电影。

　　没有十全十美的模型，这个矩阵分解模型也有缺点，我们称之为cool-start问题，即对于一个新用户（没有给任何电影评分）或者一部新电影（没有被任何用户评分），我们就无法找到合适的Ｌ和Ｒ。　

更进一步的思考

　　在前面的讨论中我们看到，当使用协同过滤方法的时候，我们可以有限的解决部分问题，在矩阵分解方法中，我们可以找到一个更优的方案，二者各有各的优缺点，那么我们能不能找到一个综合的方法呢？
　　可以考虑这样，矩阵分解方法对于cool-start问题难以解决，这时候我们可以现实用分类方法，协同过滤方法来对用户进行推荐，随着用户数据的积累，我们们慢慢的过渡到矩阵分解方法。这个思想非常简单，我们们做的仅仅是在这两个方法之间慢慢切换，这是一种非常普遍的混合模型思想。每个实用的推荐系统都不可能仅仅用一种方法，事实上可能使用上百种模型一起解决问题。混合思想用处很大，我们要体会这种思想，在我们自己构建系统时，我们需要根据实际情况选择合适的方法组合。
　　

如何确定模型的好坏

　　定义：
　　 Recall rate=喜欢并且推荐的商品喜欢的商品数量
　　 Precision rate=喜欢并且推荐的商品推荐的商品数量
　　
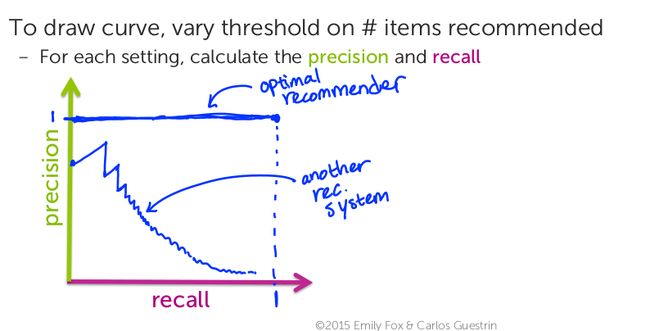
　　则我们用曲线下方的面积来比较模型的好坏，面积越大的模型效果越好。