卷积神经网络系列之softmax loss对输入的求导推导

我们知道卷积神经网络（CNN）在图像领域的应用已经非常广泛了，一般一个CNN网络主要包含卷积层，池化层（pooling），全连接层，损失层等。虽然现在已经开源了很多深度学习框架（比如MxNet，Caffe等），训练一个模型变得非常简单，但是你对损失函数求梯度是怎么求的真的了解吗？相信很多人不一定清楚。虽然网上的资料很多，但是质量参差不齐，常常看得眼花缭乱。为了让大家少走弯路，特地整理了下这些知识点的来龙去脉，希望不仅帮助自己巩固知识，也能帮到他人理解这些内容。

这一篇主要介绍softmax loss对输入的求导（或者叫cross entropy loss function对输入的求导），算是网络里面比较难懂的一块内容，公式较多，但是很容易看懂，需要静下心来看。

接下来我会先介绍softmax对输入求导的推导过程，然后给出softmax loss对输入的求导推导。

先推导softmax对输入的求导：
回顾下：卷积神经网络系列之softmax，softmax loss和cross entropy介绍的softmax，就是下面这个公式：

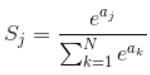
N表示类别数，a表示全连接层的输出向量，aj表示向量a的第j个值。

那么如果将Si对aj求导，就是下面这个式子：

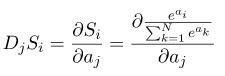
注意到这个式子中Si的分子的指数是ai，而求导对象是aj，因此在求导的时候就存在i==j和i！=j这两种情况。另外这里用DjSi表示Si对aj的导数，这种表示方式后面会用到。

当i==j时，求导的公式是下面这样的：

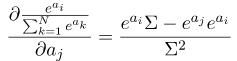
这个是比较基本的求导，不要觉得字符多就很难，虽然我一开始也是这么认为的。如果不熟悉的话应该要过一下简单的微积分（提示两点：1、e^ai对ai的导数还是e^ai；2、∑表示e^a1+e^a2+…+e^aN，因此对∑求导时，只有e^aj对aj的导数不为0，其他都是0）

因此，化简这个求导公式就得到下面这个式子的结果。这里第三个等式是怎么得到的呢？请看上面的第一个公式，也就是softmax那个公式，你就知道S是softmax的输出。

当i！=j时，求导公式和前面同理是下面这样的：

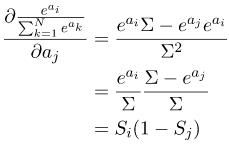
因此整合下i==j和i！=j的情况，就得到Si对aj的导数如下：

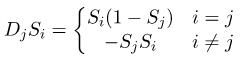
——————————————–华丽的分割线———————————————–

前面介绍的是softmax对输入的求导推导过程，我们的目的是损失函数对输入求导，因为这个过程需要用到softmax对输入的求导，所以就先介绍了。softmax loss的公式是下面这样的，这个在博文：卷积神经网络系列之softmax，softmax loss和cross entropy里也介绍过了。我们知道模型在训练的时候先进行前向计算，得到在当前模型参数下的预测值，也就是下式的S；然后计算这次预测的损失，也就是下式的L；然后反向传递损失并计算梯度（这个梯度包含损失对参数的梯度和对该层输入的梯度）；最后再正向更新参数。

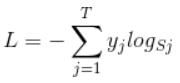
然后就是softmax对输入的求导，这里直接给出结论，因为在分割线之前都在推导这个求导的过程。

上面两步准备好了损失函数L和softmax对输入的导数，然后就可以计算损失函数对输入的导数了。下面这个式子就是计算损失函数L对输入xi的导数。这个式子中的第一、二个等号比较好理解。第三个等号就用到了上面pj对xi求导的结论，第三个等号结果的左半部分是i==k的时候pk对xi的导数，求导得到的pk和原来的1/pk相乘约掉了，对yk的求和由于i==k所以只剩下yi；右半部分是i！=k的时候pk对xi的导数，注意右半部分的∑底下的k！=i。第四、五个等号也比较好理解。第六个等号是将yipi合并到∑里面。最后一个等号的成立是建立在假设∑yk=1的前提下，这个对于常见的单标签分类任务而言都是成立的。

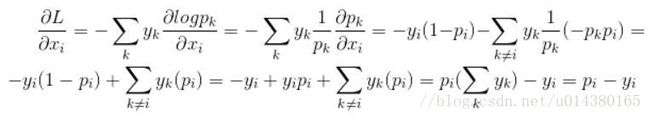
因此假设一个5分类任务，一张图像经过softmax层后得到的概率向量p是[0.1,0.2,0.25,0.4,0.05]，真实标签y是[0,0,1,0,0]，那么损失回传时该层得到的梯度就是p-y=[0.1,0.2,-0.75,0.4,0.05]。这个梯度就指导网络在下一次forward的时候更新该层的权重参数。

综上就是softmax loss对输入的求导推导。