残差网络(Deep Residual Learning for Image Recognition)

题外话：
了解ResNet的都会清楚他是应用于CNN的，按说我一个做nlp的不应该是用RNN、LSTM、gru吗？是的CNN 确实是在图像处理上应用更常见，但是现在CNN在很多文本处理、文本分类里面用到（n-gram），并展现出了相当不错的效果，所以嘛，我也要学习啦~
2019.2.22更新：其实除了CNN用在nlp里面可以使用残差网络，其实在含有RNN的一些模型里面我觉得也用到了这种思想，比如bidaf、QAnet里面的C2Q（$\hat{U}$）、Q2C（$\hat{H}$）就是和经过原来的context matrix($H$)做了concatation,虽然不像resnet一样相加，但是我觉得思想是一样的~ 另外，在transformer、bert、qanet中更是直接用了residual部分，所以resnet不仅仅是用在了cv，更在nlp广泛运用~

paper link:点击下载

1. 引言

• 网络的深度为什么重要？
  因为CNN能够提取low/mid/high-level的特征，网络的层数越多，意味着能够提取到不同level的特征越丰富。并且，越深的网络提取的特征越抽象，越具有语义信息。
• 为什么不能简单地增加网络层数？
  对于原来的网络，如果简单地增加深度，会导致梯度弥散或梯度爆炸。
  对于该问题的解决方法是正则化初始化和中间的正则化层（Batch Normalization），这样的话可以训练几十层的网络。（原文：This problem,however, has been largely addressed by normalized initialization and intermediate normalization layers, which enable networks with tens of layers to start converging for stochastic gradient descent (SGD) with backpropagation）
  虽然通过上述方法能够训练了，但是又会出现另一个问题，就是退化问题，网络层数增加，但是在训练集上的准确率却饱和甚至下降了。这个不能解释为overfitting，因为overfit应该表现为在训练集上表现更好才对。
  退化问题说明了深度网络不能很简单地被很好地优化。

作者通过实验：通过浅层网络+ y=x 等同映射构造深层模型，结果深层模型并没有比浅层网络有等同或更低的错误率，推断退化问题可能是因为深层的网络并不是那么好训练，也就是求解器很难去利用多层网络拟合同等函数。
更直白的说，为什么层数多了准确率反而下降？
一个是56层的网络一个是20层的网络，从原理上来说其实56层网络的解空间是包括了20层网络的解空间的，换而言之也就是说，56层网络取得的性能应该大于等于20层网络的性能的。但是从训练的迭代过程来看，56层的网络无论从训练误差来看还是测试误差来看，误差都大于20层的网络（这也说明了为什么这不是过拟合现象，因为56层网络本身的训练误差都没有降下去）。导致这个原因就是虽然56层网络的解空间包含了20层网络的解空间，但是我们在训练网络用的是随机梯度下降策略，往往解到的不是全局最优解，而是局部的最优解，显而易见56层网络的解空间更加的复杂，所以导致使用随机梯度下降算法无法解到最优解。

2. 怎么解决退化问题？

2.1.直观理解

深度残差网络。如果深层网络的后面那些层是恒等映射，那么模型就退化为一个浅层网络。那现在要解决的就是学习恒等映射函数了。 但是直接让一些层去拟合一个潜在的恒等映射函数H(x) = x，比较困难，这可能就是深层网络难以训练的原因。但是，如果把网络设计为H(x) = F(x) + x,如下图。我们可以转换为学习一个残差函数F(x) = H(x) - x. 只要F(x)=0，就构成了一个恒等映射H(x) = x. 而且，拟合残差肯定更加容易。
理论上，对于“随着网络加深，准确率下降”的问题，Resnet提供了两种选择方式，也就是identity mapping和residual mapping，如果网络已经到达最优，继续加深网络，residual mapping将被push为0，只剩下identity mapping，这样理论上网络一直处于最优状态了，网络的性能也就不会随着深度增加而降低了。

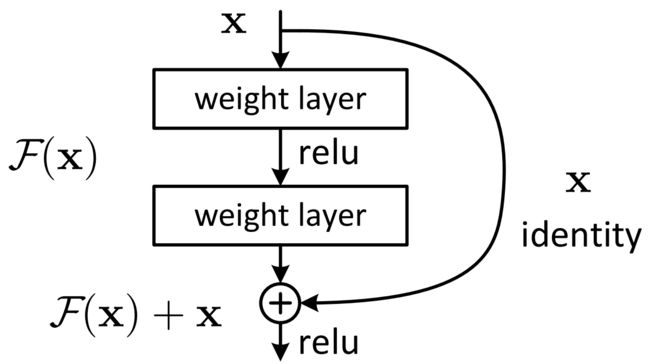图1 Shortcut Connection

一个通俗的理解：
F是求和前网络映射，H是从输入到求和后的网络映射。比如把5映射到5.1，那么引入残差前是F’(5)=5.1，引入残差后是H(5)=5.1, H(5)=F(5)+5, F(5)=0.1。这里的F’和F都表示网络参数映射，引入残差后的映射对输出的变化更敏感。比如s输出从5.1变到5.2，映射F’的输出增加了1/51=2%，而对于残差结构输出从5.1到5.2，映射F是从0.1到0.2，增加了100%。明显后者输出变化对权重的调整作用更大，所以效果更好。残差的思想都是去掉相同的主体部分，从而突出微小的变化，看到残差网络我第一反应就是差分放大器…
参考链接：知乎问答
这里我们再来延伸思考一下，残差的思想其实还是很像我们高数中学的泰勒公式的，在泰勒公式中，我们往后相加的是更高阶的多项式，这里加的也可以考虑成更高阶的多项式

这种残差学习结构可以通过前向神经网络+shortcut连接实现，如结构图所示。而且shortcut连接相当于简单执行了同等映射，不会产生额外的参数，也不会增加计算复杂度。 而且，整个网络可以依旧通过端到端的反向传播训练。
该模型在几个大型比赛中都拿到了1st，所以其威力还是可以的。

2.2.公式推导(敲黑板，划重点)

残差结构可简单的写成如下形式：
$$x_{l+1}=x_l+F(x_l,W_l)$$

通过递归，可以得到任意深层单元L特征的表达：
$$x_L=x_l+\sum _{i=l}^{L-1}F(x_i,W_i)$$
即对于任意深的单元L的特征$x_L$可以表达为浅层单元l的特征$x_l$加上一个形如${\sum }_{i=l}^{L-1}F$的残差函数，这表明了任意单元L和l之间都具有残差特性。
同样的，对于任意深的单元L，它的特征$x_L=x_0+{\sum }_{i=0}^{L-1}F(x_i,W_i)$，即为之前所有残差函数输出的总和再加上x0。对比平原网络(plain network)，其特征$x_L$是一系列矩阵向量的乘积，也就是${\prod }_{i=0}^{L-1}{W}_i{x}_0$（为了便于理解，先不添加bias），而求和的计算量远远小于求积的计算量。

对于反向传播，假设损失函数为E，根据反向传播的链式法则可以得到：
$$\frac{\partial \epsilon }{\partial {\mathbf{x}}_l}=\frac{\partial \epsilon }{\partial {\mathbf{x}}_L}\frac{\partial {\mathbf{x}}_L}{\partial {\mathbf{x}}_l}=\frac{\partial \epsilon }{\partial {\mathbf{x}}_L}(1+\frac{\partial }{\partial {\mathbf{x}}_l}\sum _{i=l}^{L-1}F({\mathbf{x}}_i,w_i))$$
我们可以发现这个导数可以被分为两部分：

• 不通过权重层的传递$\frac{\partial \epsilon }{\partial {\mathbf{x}}_L}$
• 通过权重层的传递$\frac{\partial \epsilon }{\partial {\mathbf{x}}_L}(\frac{\partial }{\partial {\mathbf{x}}_l}{\sum }_{i=l}^{L-1}F({\mathbf{x}}_i,w_i))$

前者保证了信号能够直接传回到任意的浅层$x_l$，同时这个公式也保证了不会出现梯度消失的现象，因为$\frac{\partial }{\partial {\mathbf{x}}_l}{\sum }_{i=l}^{L-1}F({\mathbf{x}}_i,w_i)$不可能为-1。

3. 残差指的是什么？

其中ResNet提出了两种mapping：一种是identity mapping，指的就是图1中”弯弯的曲线”，另一种residual mapping，指的就是除了”弯弯的曲线“那部分，所以最后的输出是 $y=F(x)+x$
identity mapping顾名思义，就是指本身，也就是公式中的x，而residual mapping指的是“差”，也就是$y-x$，所以残差指的就是$F(x)$部分。

4. ResNet结构

它使用了一种连接方式叫做“shortcut connection”，顾名思义，shortcut就是“抄近道”的意思，看下图我们就能大致理解：

图1 Shortcut Connection Shortcut Connection的两种方式：

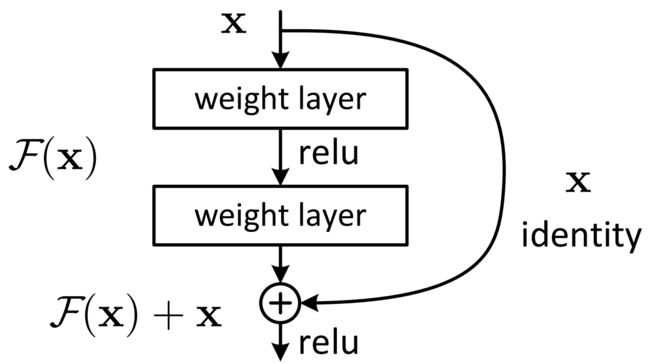
• shortcut同等维度映射，F(x)与x相加就是就是逐元素相加
  $$y=F(x,W_i)+x$$
  $$F=W_2\sigma (W_{1}x)$$
• 如果两者维度不同，需要给x执行一个线性映射来匹配维度
  $$y=F(x,W_i)+W_{s}x$$
  $$F=W_2\sigma (W_{1}x)$$

用卷积层进行残差学习：以上的公式表示为了简化，都是基于全连接层的，实际上当然可以用于卷积层。加法随之变为对应channel间的两个feature map逐元素相加。
设计网络的规则：

1. 对于输出feature map大小相同的层，有相同数量的filters，即channel数相同；
2. 当feature map大小减半时（池化），filters数量翻倍。
   对于残差网络，维度匹配的shortcut连接为实线，反之为虚线。维度不匹配时，同等映射有两种可选方案：

• 直接通过zero padding 来增加维度（channel）。
• 乘以W矩阵投影到新的空间。实现是用1x1卷积实现的，直接改变1x1卷积的filters数目。这种会增加参数。

对于同等映射维度不匹配时，匹配维度的两种方法，zero padding是参数free的，投影法会带来参数。作者比较了这两种方法的优劣。实验证明，投影法会比zero padding表现稍好一些。因为zero padding的部分没有参与残差学习。实验表明，将维度匹配或不匹配的同等映射全用投影法会取得更稍好的结果，但是考虑到不增加复杂度和参数free，不采用这种方法。

---

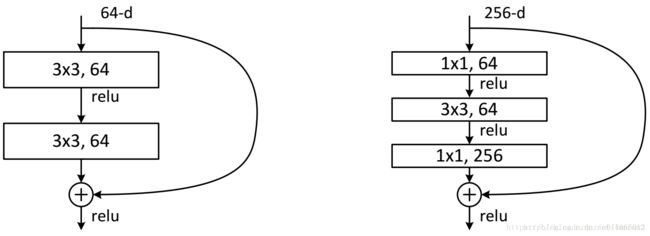
上图是文章里面的图，我们可以看到一个“弯弯的弧线“这个就是所谓的”shortcut connection“，也是文中提到identity mapping，这张图也诠释了ResNet的真谛，当然大家可以放心，真正在使用的ResNet模块并不是这么单一，文章中就提出了两种方式：

图2 两种ResNet设计

这两种结构分别针对ResNet34（左图）和ResNet50/101/152（右图），一般称整个结构为一个”building block“。其中右图又称为”bottleneck design”，目的一目了然，就是为了降低参数的数目，第一个1x1的卷积把256维channel降到64维，然后在最后通过1x1卷积恢复，整体上用的参数数目：1x1x256x64 + 3x3x64x64 + 1x1x64x256 = 69632，而不使用bottleneck的话就是两个3x3x256的卷积，参数数目: 3x3x256x256x2 = 1179648，差了16.94倍。 (这部分如果看起来比较生涩的话，可以先跳过，待会看完5.2小节再回来看就简单了~)
对于常规ResNet，可以用于34层或者更少的网络中，对于Bottleneck Design的ResNet通常用于更深的如101这样的网络中，目的是减少计算和参数量（实用目的）。

5. 细节问题

5.1 如图1所示，如果F(x)和x的channel个数不同怎么办，因为F(x)和x是按照channel维度相加的，channel不同怎么相加呢？

针对channel个数是否相同，要分成两种情况考虑，如下图：

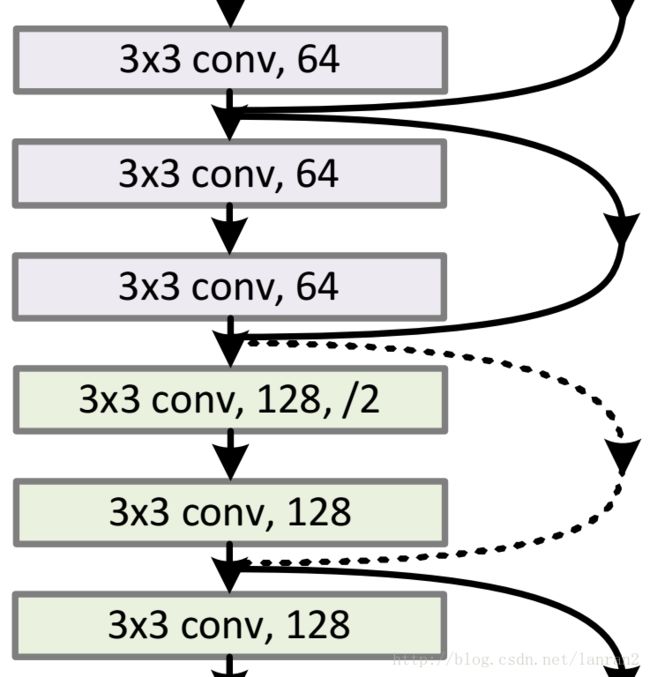图3 两种Shortcut Connection方式 如图3所示，我们可以清楚的”实线“和”虚线“两种连接方式， 实线的的Connection部分(”第一个粉色矩形和第三个粉色矩形“)都是执行3x3x64的卷积，他们的channel个数一致，所以采用计算方式：

$$y=F(x)+x$$
虚线的的Connection部分(”第一个绿色矩形和第三个绿色矩形“)分别是3x3x64和3x3x128的卷积操作，他们的channel个数不同(64和128)，所以采用计算方式：
$$y=F(x)+Wx$$
其中W是卷积操作（用128个(3x3)x64的filter），用来调整x的channel维度的；

5.2 计算细节

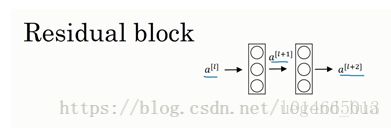
这里的Residual block（取自deeplearning.ai）按说和上面building block是一个东西

这是一个两层神经网络，在l层进行激活，得到a[l+1]，再次进行激活，两层之后得到a[l+2]。计算过程是从a[l]开始，首先进行线性激活，根据这个公式：z=wx+b，通过算出z，即x(图中a[l])乘以权重矩阵w，再加上偏差因子b。然后通过ReLU非线性激活函数得到a，计算得出a[l+1]。接着再次进行线性激活，依据等式z = wx+b，最后根据这个等式再次进行ReLu非线性激活，即，这里的是指ReLU非线性函数，得到的结果就是a[l+2]。换句话说，信息流从到需要经过以上所有步骤，即这组网络层的主路径。

在残差网络中有一点变化，我们将直接向后，拷贝到神经网络的深层，在ReLU非线性激活函数前加上，这是一条捷径。a[l]的信息直接到达神经网络的深层，不再沿着主路径传递，这就意味着最后这个等式(a[l+1]=g(wa[l]+b))去掉了，取而代之的是另一个ReLU非线性函数，仍然对a[l+1]进行g函数处理，但这次要加上a[l]，即：a[l+2]=g(wa[l+1]+b+a[l])，也就是加上的这个产生了一个残差块。

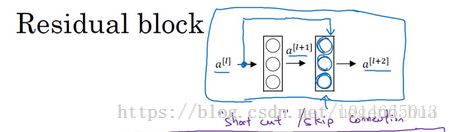
在上面这个图中，我们也可以画一条捷径，直达第二层。实际上这条捷径是在进行ReLU非线性激活函数之前加上的，而这里的每一个节点都执行了线性函数和ReLU激活函数。所以插入的时机是在线性激活之后，ReLU激活之前。除了捷径，你还会听到另一个术语“跳跃连接”，就是指跳过一层或者好几层，从而将信息传递到神经网络的更深层。

这里用的是全连接层举例的，但是如果在CNN中，如果是一层还想就变成了线性函数了，所以一般选用的是两层或者多层~~~

5.3.网络中的网络以及 1×1 卷积

在架构内容设计方面，其中一个比较有帮助的想法是使用1×1卷积。也许你会好奇，1×1的卷积能做什么呢？不就是乘以数字么？听上去挺好笑的，结果并非如此，我们来具体看看。

过滤器为1×1，这里是数字2，输入一张6×6×1的图片，然后对它做卷积，起过滤器大小为1×1×1，结果相当于把这个图片乘以数字2，所以前三个单元格分别是2、4、6等等。用1×1的过滤器进行卷积，似乎用处不大，只是对输入矩阵乘以某个数字。但这仅仅是对于6×6×1的一个通道图片来说，1×1卷积效果不佳。

如果是一张6×6×32的图片，那么使用1×1过滤器进行卷积效果更好。具体来说，1×1卷积所实现的功能是遍历这36个单元格，计算左图中32个数字和过滤器中32个数字的元素积之和，然后应用ReLU非线性函数。

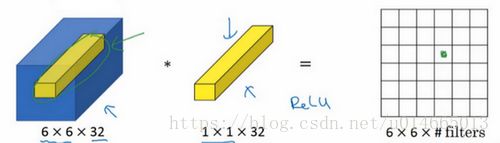
我们以其中一个单元为例，它是这个输入层上的某个切片，用这36个数字乘以这个输入层上1×1切片，得到一个实数，像这样把它画在输出中。

这个1×1×32过滤器中的32个数字可以这样理解，一个神经元的输入是32个数字（输入图片中左下角位置32个通道中的数字），即相同高度和宽度上某一切片上的32个数字，这32个数字具有不同通道，乘以32个权重（将过滤器中的32个数理解为权重），然后应用ReLU非线性函数，在这里输出相应的结果。

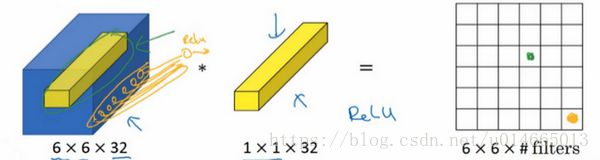
一般来说，如果过滤器不止一个，而是多个，就好像有多个输入单元，其输入内容为一个切片上所有数字，输出结果是6×6过滤器数量。

所以1×1卷积可以从根本上理解为对这32个不同的位置都应用一个全连接层，全连接层的作用是输入32个数字（过滤器数量标记为，在这36个单元上重复此过程）,输出结果是6×6×#filters（过滤器数量），以便在输入层上实施一个非平凡（non-trivial）计算。

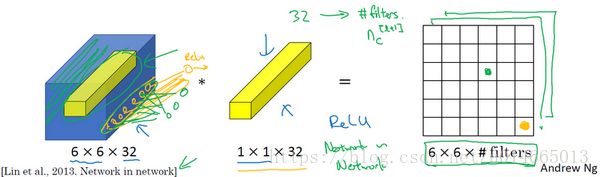
这种方法通常称为1×1卷积，有时也被称为Network in Network，在林敏、陈强和杨学成的论文中有详细描述。虽然论文中关于架构的详细内容并没有得到广泛应用，但是1×1卷积或Network in Network这种理念却很有影响力，很多神经网络架构都受到它的影响

举个1×1卷积的例子，相信对大家有所帮助，这是它的一个应用。
假设这是一个28×28×192的输入层，你可以使用池化层压缩它的高度和宽度，这个过程我们很清楚。但如果通道数量很大，该如何把它压缩为28×28×32维度的层呢？你可以用32个大小为1×1的过滤器，严格来讲每个过滤器大小都是1×1×192维，因为过滤器中通道数量必须与输入层中通道的数量保持一致。但是你使用了32个过滤器，输出层为28×28×32，这就是压缩通道数（）的方法，对于池化层我只是压缩了这些层的高度和宽度。

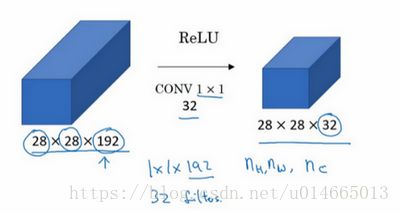
在之后我们看到在某些网络中1×1卷积是如何压缩通道数量并减少计算的。当然如果你想保持通道数192不变，这也是可行的，1×1卷积只是添加了非线性函数，当然也可以让网络学习更复杂的函数，比如，我们再添加一层，其输入为28×28×192，输出为28×28×192。

1×1卷积层就是这样实现了一些重要功能的（doing something pretty non-trivial），它给神经网络添加了一个非线性函数，从而减少或保持输入层中的通道数量不变，当然如果你愿意，也可以增加通道数量。

6.ResNet50和ResNet101

这里把ResNet50和ResNet101特别提出，主要因为它们的出镜率很高，所以需要做特别的说明。给出了它们具体的结构：

表2，Resnet不同的结构

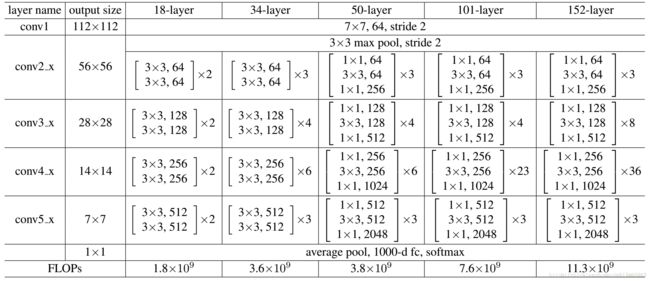
首先我们看一下表2，上面一共提出了5中深度的ResNet，分别是18，34，50，101和152，首先看表2最左侧，我们发现所有的网络都分成5部分，分别是：conv1，conv2_x，conv3_x，conv4_x，conv5_x，之后的其他论文也会专门用这个称呼指代ResNet50或者101的每部分。

拿101-layer那列，我们先看看101-layer是不是真的是101层网络，首先有个输入7x7x64的卷积，然后经过3 + 4 + 23 + 3 = 33个building block，每个block为3层，所以有33 x 3 = 99层，最后有个fc层(用于分类)，所以1 + 99 + 1 = 101层，确实有101层网络；

注：101层网络仅仅指卷积或者全连接层，而激活层或者Pooling层并没有计算在内；
这里我们关注50-layer和101-layer这两列，可以发现，它们唯一的不同在于conv4_x，ResNet50有6个block，而ResNet101有23个block，查了17个block，也就是17 x 3 = 51层。

7.相关的工作

7.1.残差表示

VALD，Fisher Vector都是是对残差向量编码来表示图像，在图像分类，检索表现出优于编码原始向量的性能。
在low-level的视觉和计算机图形学中，为了求解偏微分方程，广泛使用的Multigrid方法将系统看成是不同尺度上的子问题。每个子问题负责一种更粗糙与更精细尺度的残差分辨率。Multigrid的一种替换方法是层次化的预处理，层次化的预处理依赖于两种尺度的残差向量表示。实验表明，这些求解器要比对残差不敏感的求解器收敛更快。

7.2.shortcut连接

普通的平原网络与深度残差网络的最大区别在于，深度残差网络有很多旁路的支线将输入直接连到后面的层，使得后面的层可以直接学习残差，这些支路就叫做shortcut。传统的卷积层或全连接层在信息传递时，或多或少会存在信息丢失、损耗等问题。ResNet 在某种程度上解决了这个问题，通过直接将输入信息绕道传到输出，保护信息的完整性，整个网络则只需要学习输入、输出差别的那一部分，简化学习目标和难度。

VGG-19、34层的平原网络、34层的深度残差网络结构对比 shortcut连接被实验和研究了很久。**Highway networks也使用了带有门函数的shortcut**。但是这些门函数需要参数，而ResNet的shortcut不需要参数。而且当Highway networks的门函数的shortcut关闭时，相当于没有了残差函数，但是ResNet的shortcut一直保证学习残差函数。而且，当Highway networks的层数急剧增加时，没有表现出准确率的上升了。总之，ResNet可以看成是Highway networks的特例，但是从效果上来看，要比Highway networks好。

参考链接

• ResNet解析
• 残差网络ResNet笔记
• ResNets和Inception的理解
• 高速路神经网络(Highway Networks)与深度残差网络(ResNet)的原理和区别