从DBSCAN算法谈谈聚类算法

DBSCAN算法

前言

最近看了一篇关于电子商务防欺诈的相关论文，其中在构建信用卡的个人行为证书中用到了DBSCAN算法。
具体内容请参看论文：
Credit card fraud detection: A fusion approach using Dempster–Shafer theory
and Bayesian learning。
我就想深入了解下这个聚类方法是怎么工作的。在思考这个具体DBSCAN算法的形成过程中，我还参看了：
1. wikipedia DBSCAN的相关介绍
2. 博文简单易学的机器学习算法——基于密度的聚类算法DBSCAN
3. 论文-A Density-Based Algorithm for Discovering Clusters
in Large Spatial Databases with Noise
等相关文献。此篇博文尝试讲清楚”物以类聚，人以群分”这个概念，DBSCAN算法中两个参数的实际物理含义，以及它背后所做的基本假设，由于这方面资料不多，因此都属于个人的猜想，不代表发明DBSCAN算法作者本身的想法，且这也是我正式学习聚类算法中的第一个算法，由于知识的局限性，如有不当，请指正。

DBSCAN

DBSCAN 是什么？

DBSCAN算法是对数据样本进行划分的聚类算法，且我们事先并不知道数据样本的标签，是一种非监督的聚类算法。在wiki pedia的定义中原文是这样的：

Density-based spatial clustering of applications with noise (DBSCAN) is a data clustering algorithm proposed by Martin Ester, Hans-Peter Kriegel, Jörg Sander and Xiaowei Xu in 1996.1 It is a density-based clustering algorithm: given a set of points in some space, it groups together points that are closely packed together (points with many nearby neighbors), marking as outliers points that lie alone in low-density regions (whose nearest neighbors are too far away). DBSCAN is one of the most common clustering algorithms and also most cited in scientific literature.

我们注意以下关键词：density-based,outliers points，这两个单词该如何理解呢？为何说该聚类算法是density-based，且数据样本中的outliers points有何作用？

DBSCAN 定义

先来看看DBSCAN一些关键概念的定义：
1. ϵ 邻域：给定对象半径 ϵ 内的区域称为该对象的 ϵ 邻域。
2. 核心对象（core points）：如果给定对象 ϵ 邻域内的样本点数大于等于MinPts，则称该对象为核心对象。
3. 直接密度可达（directly density-reachable）：给定一个对象集合D，如果p在q的 ϵ 的邻域内，且q是一个核心对象，则我们说对象p从对象q出发是直接密度可达的。
4. 密度可达（density-reachable）：对于样本集合D，如果存在一个对象链 P1,P2,...,Pn,P1=q,Pn=p ，对于 Pi∈D,1≤i≤n ， Pi+1 是从 Pi 关于 ϵ 和MinPts直接密度可达，则对象p是从对象q关于 ϵ 和MinPts密度可达的。
5. 密度相连（density-connected）：如果存在对象 o∈D ，使对象p和q都是从o关于 ϵ 和MinPts密度可达的，那么对象p到q是关于 ϵ 和MinPts密度相连的。

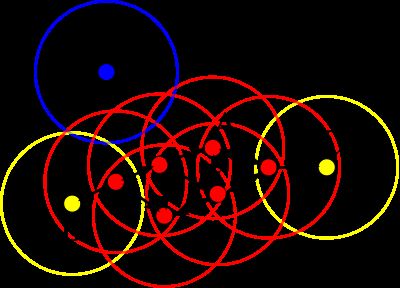
根据上图，咱们分别来解释这五条定义。
1. 以某个数据样本点作为圆心，以 ϵ 为半径画圆，每个圆所圈的区域就是 ϵ 邻域。直观上来说，有多少个数据样本点，就有多少个邻域。
2. 核心对象的概念还需要强化一下，数学形式的定义如下： Nϵ(p)={q∈D|dist(p,q)≤ϵ} ，且 p∈Nϵ(p),|Nϵ(p)|≥MinPts ，满足上述两个条件的p为核心对象。从同图中来说，假设MinPts是3，红色的点都属于核心对象。
3. 如A点所画出的圈圈内的其他任何红色点都属于直接密度可达。
4. 密度可达的关系相对弱一点，除A点邻域内的其他红色点与A的关系均属于密度可达。
5. 个人觉得密度相连与密度可达是一个概念，只是说考虑的角度不同，从A出发，能够密度可达的任意两个点都属于密度相连。

有了这些基础概念的定义后，我们就可以对数据样本进行聚类了，具体的算法如下：

算法（DBSCAN）:

输入：半径 ϵ ，给定点在 ϵ 邻域内成为核心对象的最小邻域点数MinPts，数据集D
输出：目标类簇集合
Repeat:
(1) 判断输入点是否为核心对象
(2) 找出核心对象的 ϵ 邻域中的所有直接密度可达点
Until 所有输入点都判断完毕
Repeat:
针对所有核心对象的 ϵ 邻域内所有直接密度可达点找到最大密度相连对象集合，中间涉及到一些密度可达对象的合并
Until 所有核心对象的 ϵ 邻域都遍历完毕

上述内容均摘自各博文，论文和wiki百科。不知道为何，看完这些内容始终不知所以然，为什么DBSCAN设置两个参数 ϵ 和MinPts就能有效地分类，算法的思路如此清晰，可是作者是如何一步步逼近正确答案的？接下来，我将结合自身思考，试着解释清楚DBSCAN的本质，从而能够帮助自己更好的使用该算法。

DBSCAN构建思路

物以类聚，人以群分

最近写了一篇决策树之理解ID3算法和C4.5算法，其中在分析信息熵的由来时，对决策树有了更深层次的认识，决策树是一种监督分类方法，在给定标签下，我们统计大量数据样本从而得到正确的决策规则。在这里我提到了很重要的一个概念是基于大量数据的统计。决策树的本质在于统计，那回过头来看看DBSCAN聚类算法，此处的数据样本没有了类别标签，即所谓的非监督学习。它属不属于统计？看图。

首先思考一个问题，数据为什么会呈现聚类这种奇怪的现象？这其实是统计学中的一个概念，即基于大数据背后，每个数据样本都有它们的不确定性。聚类需要满足两个条件：第一，类与类之间有一个影响它们本质的gap，也就是说在2维世界中两堆数据是有一定的间距的。影响间距的本质原因，便是现实世界中影响人们区分这两类事物的判别依据，只是在数据的坐标轴世界中我们以distance来衡量；第二，每个类在自己的群体内，有某种微小的不确定性影响着它们的分布，但不足以跨越那个gap。即这些微小的不确定性，导致了数据样本在某个特定的样本空间附近随机出现，从而在坐标轴中能够看到大量数据堆积在一块。

现在，我们来考虑一个实际的问题来理解什么是聚类。

某两所高校为了迎战高考，准备一次联合模拟考，现在我们已知了两所学校各学生的数学成绩，如下图所示。现在我们希望能够根据这些数据来区分这些学生都属于哪所高校，假设两高校学生的平均水平未知。

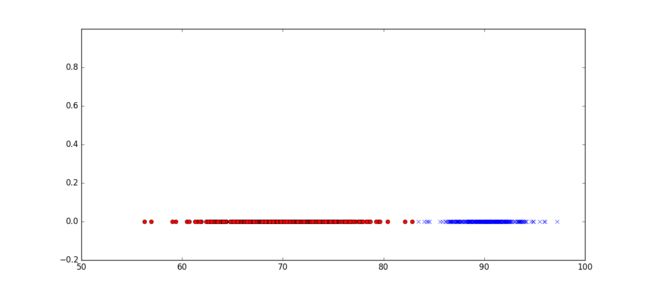
这里面，我们已经对数据样本做了区分。红色点代表A校学生的分数分布情况，蓝色点代表B校学生的分数分布情况。那么图中的信息告诉我们什么样的事实？

很明显，数据出现了某种群聚现象。A校学生的平均分集中在70分，而B校学生的成绩集中在90分，并且分别向两边扩散，且分布密度逐渐递减。在83分这个边界上两者有所交叉。我们在统计成绩时，往往一个群体的成绩分布情况就呈现于类似的分布，由大量数据统计得，其背后是符合高斯模型的。（难道不能是其他分布？）这就是所谓的“物以类聚，人以群分”。如A校，B校问题，在历史进程中，A校，B校在招人时，就有一种自然规则，中考成绩优异的进入B校，而中考稍差的进入A校。这种历史因素我们虽然观测不到，却着实影响了未来成绩的分布情况。

现在，我们从考试这个例子中解释为何会出现gap，以及gap是如何帮助我们区分A校B校的学生。

一张理想的数学卷子，它的难易程度是不一样的，为了方便阐述问题，我们假设一张数学卷子有80道易答题，每道1分。一道10分的中等难度题，和10道1分的有难度题。将这张数学卷子给A,B校考生做后，得到了如下的数据分布。问，哪些学生是A校，哪些学生是B校？

我们知道B校在历史上的学生是优于A校的学生，所以我们可以简单认为，对于80分题目他们回答的正确率为100%，大题10分准确率80%，10道有难度的题该校学生的平均回答准确率在50%。而A校学生，80分题目的回答的正确率为80%，大题10分正确率为10%，10道有难度题回答准确率在1%。当然上述假定是没有任何依据的，这需要真正的去统计该学校每一道题的回答准确率才能得出准确的数字，这里是为了方便解释背后的概率模型。

对于B校的学生，80分的题目对他们来说都不是事，因此绝大多数的学生成绩必然高于80分，且对于中等难度的题，大部分学生依然能够完成。所以成绩都80朝上，甚至90朝上。可A校的学生，中等难度的10分题是他们的一个障碍，以他们的水平几乎没人能够完成这道题，由此他们的成绩只能80分朝下。这10分便是数据的gap，天然的分割了A校和B校的学生。

但聚类的另外一个特征是大家都会聚集在一块，这又是什么原因造成的呢？前文讲了一种不确定性，不确定性来源于概率统计的不确定性。拿A校学生的数学成绩分布来讲（B校依此类推），80分的题，他们准确率为80%，那么从概率上来说，全部答对的可能性是相当小的。我们可以写出在80道题中，答对n道题的概率：

P(n|θ=0.8)=Cn800.8n0.280−n

由此得到了，如下的伯努利概率分布函数：

红色长条为A校学生分数出现的概率，蓝色长条为B校学生各分数出现的概率。当统计的样本很大时，伯努利概率分布函数将等价于高斯分布函数。

这张图很好的解释了类的群聚效应，虽然每个学生是独特的，但由于他们先天的资质和后天的努力在一个类群中相差不多，导致做数学题时，每个群体对于不同难度的题的回答准确率不同,可在群体内正确率是相近的。而又由于并非百分之百的回答准确率，这种不确定性导致了大量数据呈现中间高，两边低的分布形态。最终有了数据样本背后的模型大都是高斯分布模型。

费了这么大劲，这是要闹哪样啊，其实说了那么多，只是为了解释聚类的两个本质特征，gap和群聚。在上图中，70分和90分附近群聚了大量数据，并分别向两边递减，而在83分左右附近，出现了一个gap。而DBSCAN就是利用了这两个特征构建出了一套算法，所谓的density-based和outlier points。

当然，在这个例子中，背后的统计模型是高斯分布，或许是这套DBSCAN算法的特例罢了，但whatever，有特例给我们研究总归没有好。我们来看看一般的高斯概率密度函数：

N(μ,δ2)=1δ2π−−√e−(x−μ)22δ2

还记得DBSCAN算法需要输入的两个参数嘛？ ϵ 和MinPts，我们逐一来解释下， ϵ 本质上是一个核心点距离一个点的距离。在前述例子中，我们可以设置 ϵ 为几？显然设置距离 1≤ϵ≤10 比较合适，因为1是每道题最小的分值，小于1的邻域是不会有任何点存在的，那为什么要小于10呢，因为我们知道了区分两类群体的关键gap在于那道中等难度的题，它的分值为10。超过10分，那在83分处很容易就将这两类群体连接在一起了（由DBSCAN算法决定）。所以也就解释了wikipedia上的一句话：

The parameters minPts and ε can be set by a domain expert, if the data is well understood.

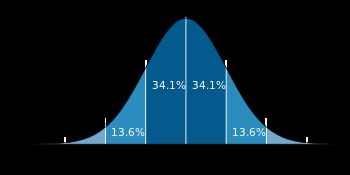
在考试问题上，我们显然是这个领域的专家，因为我们知道了影响数据背后最本质的原因，即考虑了试卷的难易程度和区分度等等。接下来我们继续来分析MinPts参数为何能够实现数据样本的分类。由高斯概率分布函数我们容易得到，越靠近对称轴的位置，数据分布越密，即在 ϵ 邻域内的数据点越多，而越靠近两边，数据分布开始变得稀疏，数据点不断减小，如下图所示。

深蓝色区域是距平均值小于一个标准差之内的数值范围。在正态分布中，此范围所占比率为全部数值之68%。根据正态分布，两个标准差之内（蓝，棕）的比率合起来为95%。根据正态分布，三个标准差之内（深蓝，橙，黄）的比率合起来为99%。

上述解释摘自博文正态分布（Normal distribution）又名高斯分布（Gaussian distribution），在这里我们重新解释一波，在相同的 ϵ 范围内，你能看到数据样本分布的概率向两边逐渐递减，在 −3δ和−2δ 附近样本量只有总数的2.1%，因此我们可以设置MinPts为样本总数的2.1%，当小于这个值，便不再是我们的core points，而是outlier points。那么深蓝和蓝色区域均为我们的核心点，也就是算法中密度相连的点，而一旦靠近高斯分布的底部，由于样本量小于一定数值，算法不再认为是核心点，转而区分了两类人群。

再看这图，结合MinPts和参数 ϵ 是不是豁然开朗了。

特征维度与类别的关系

刚才数学成绩分布，只是用来区分优等生和中等生。也就是说，一维的特征向量，就能够进行最简单的聚类。假设我们不仅要区分优等生和中等生，我们还想知道哪些学生是聪明的？哪些学生是勤奋的？显然，一维数据是不够表达的，在对学生进行统计时，可以加入其他特征向量，如学习时间。

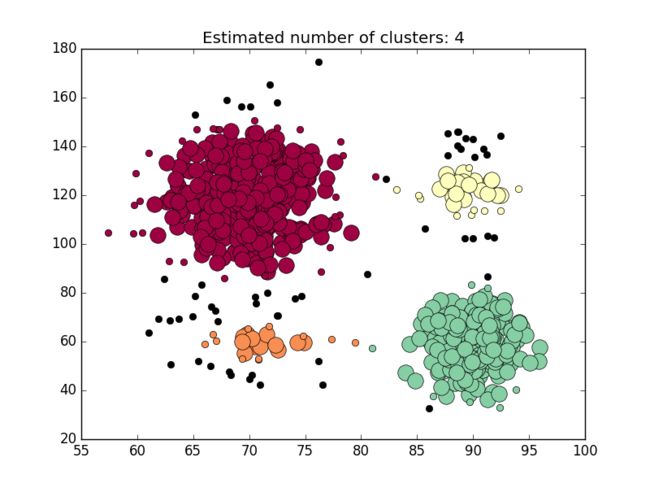
y轴代表了学生的学习时间，数值越高表示学习时间越多。有了第二维特征，我们可以发现数据在特征空间中隐约呈现出了四类。而恰巧这些数据是能够被区分成四类数据：
1. 红点可以表示为勤奋但由于成绩中等，表示为笨蛋
2. 绿点可以表示为不好学但成绩中等，表示为一般聪明
3. 蓝叉可以表示为好学且成绩优异，表示为一般聪明
4. 黄叉可以表示为不好学但成绩优异，表示为非常聪明

我仔细思考了数据映射到二维后的变化过程，我们可以发现两点：
第一，数据样本由一维的两类，变成了在高维度的四类。这反映了一个什么样的事实？增加特征维度可以拉开原来的数据样本，从而区分在低维无法区分的一些特性。在二维空间，我们便能区分聪明程度了。那是否意味着取任何特征都能把数据拉开？显然这是不可能的，如果我们取学生的身高，很有可能数据是无法被拉开的。哪怕被拉开，你想想，身高+成绩，映射到现实世界对应的是什么样的类别标签？不是我们不去探究，而是探究它没有意义。

第二，从低维变高维的过程中，我们发现我们的类别标签发生了质的变化，什么意思呢？在一维中我们类别可以表示为优等生和中等生，也可以表示为B校生和A校生，然而在二维的世界中，类别标签发生了变化，显然表示成优等生和中等生不太合适，由于衡量的特征为学习时间，因此我们的标签也可以相应的上升一个维度，即聪明程度。所以说，在研究某一个分类问题时，并非想加入什么特征就加的做法一定是最好的，往往当特征不符合人类的认知时，你的聚类结果是没有意义的。

我们在举一个常见的生活问题来理解特征与聚类的关系，如我们有一堆数据，但我们只知道这些数据的颜色，分别为红色，绿色，白色。请告诉我你能聚类出什么来？红色 = 苹果，绿色 = 西瓜，白色 = 白瓜，那我可以告诉你，红色 = 胡萝卜，绿色 = 黄瓜，白色 = 白萝卜。可以不，所以说简单的颜色是无法区分这些类别的，我们只能在低维感性的认识到，红色 = 红色的东西。那行，我们再加入一个特征，特征向量变成(颜色，形状)，好了，假定物理世界中只存在这六样事物，那么我们就能区分了，红色+圆形＝苹果，红色+长条=胡萝卜，以此类推。在二维的世界中，我们从感性的认识变成具象的事物。一堆数据从一维的三类分成了二维的六类，标签从有颜色的东西变成更加具象的事物，这就是特征维度与类别的关系。

上述算法还存在一个明显的问题，即在衡量聪明程度时，绿点和蓝叉在本质上应该是一样的，然而数据把它们给区分开了，从而导致它们隶属于两个不同的类别，有待思考和解决。

Code Time

光说不练假本事，有了数据，我们就来实战一把。模拟数据生成：

import numpy as np
import matplotlib.pyplot as plt

# A校生
mu1, sigma1 = 70, 4.2
x1 = mu1 + sigma1 * np.random.randn(400)

iq_mu1,iq_sigma1 = 120,15 # 学习时间长
iq_mu2,iq_sigma2 = 60,10  # 学习时间短

tmp1 = iq_mu1 + iq_sigma1 * np.random.randn(350)
tmp2 = iq_mu2 + iq_sigma2 * np.random.randn(50)

y1 = np.append(tmp1,tmp2)

# B校生
mu2,sigma2 = 90,2.1
x2 = mu2 + sigma2 * np.random.randn(300)

tmp3 = iq_mu1 + iq_sigma1 * np.random.randn(50)
tmp4 = iq_mu2 + iq_sigma2 * np.random.randn(250)

y2 = np.append(tmp3,tmp4)

# 水平组合
dataSet1 = np.column_stack((x1,y1))
dataSet2 = np.column_stack((x2,y2))

dataSet = np.vstack((dataSet1,dataSet2))

这里我们分别取 ϵ=5 和MinPts =10，利用sklearn中的DBSCAN算法：

# DBSCAN算法
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
from sklearn.preprocessing import StandardScaler

db = DBSCAN(eps=5, min_samples=10).fit(dataSet)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_

# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)


import matplotlib.pyplot as plt

# Black removed and is used for noise instead.
unique_labels = set(labels)
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))
for k, col in zip(unique_labels, colors):
    if k == -1:
        # Black used for noise.
        col = 'k'

    class_member_mask = (labels == k)

    xy = dataSet[class_member_mask & core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col,
             markeredgecolor='k', markersize=14)

    xy = dataSet[class_member_mask & ~core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col,
             markeredgecolor='k', markersize=6)

plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

得到的分类图如下：

当 ϵ=12 和MinPts =10，得到如下分类图：

显然 ϵ 跨越了gap，所以导致分类失败。

同样的当 ϵ=5 和MinPts =3，得到如下分类图：

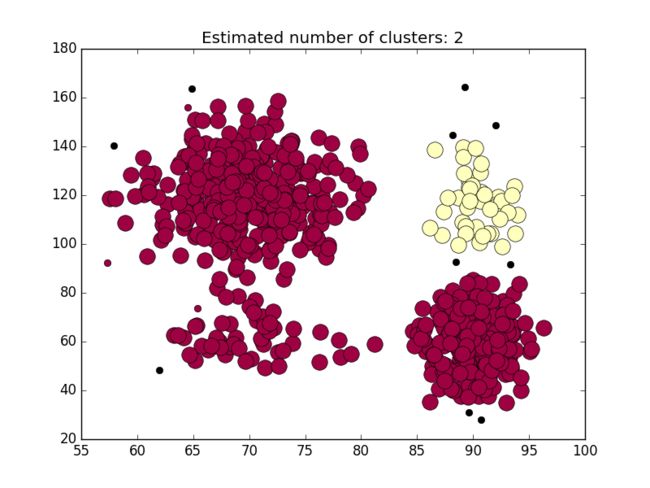
降低邻域内的样点数同样能导致分类失败。

所以说，DBSCAN算法很依赖参数的设置，在特定领域参数的设置需要领域专家来完成，而我等小菜还是乖乖的研究算法吧。

自己实现的DBSCAN版本

# function to calculate distance
def calDistance(p1,p2):
    return ((p1[0]-p2[0])**2+(p1[1]-p2[1])**2)**(0.5)

# epsilon , MinPts
epsi = 10
minPts = 8

# find out the core points
other_points = []
core_points = []
plotted_points =[]
all_points = []

# array 转 list
for point in dataSet:
    all_points.append(list(point))

# find core points
for point in all_points:
    point.append(0)
    total =0

    #  计算与其他点的距离
    for otherPoint in all_points:
        distance = calDistance(otherPoint,point)
        if distance <= epsi:
            total +=1

    if total > minPts:
        core_points.append(point)
        plotted_points.append(point)
    else:
        other_points.append(point)

# find border points
border_points =[]

# 从other_points中找寻离核心点距离小于epsi的点
for core in core_points:
    for other in other_points:
        if calDistance(core,other) <= epsi:
            border_points.append(other)
            plotted_points.append(other)

# implement the algorithm
cluster_label = 0

# 只是标记了核心点，但还没有形成簇
for point in core_points:
    if point[2] ==0: # 没有遍历过的点
        cluster_label +=1
        point[2] = cluster_label # 形成了簇

    # plotted_points 包含core_points and border_points
    for point2 in plotted_points:
        distance = calDistance(point2,point)
        # 针对那些还没形成簇的点 且 离刚形成簇的点的核心距离小于epsi，则归为一类
        if point2[2] ==0 and distance <= epsi:
            point2[2] = point[2]

# after the points are assigned correnponding labels,we group them
cluster_list = defaultdict(lambda:[[],[]])
# 记录了类别信息
for point in plotted_points:
    cluster_list[point[2]][0].append(point[0])
    cluster_list[point[2]][1].append(point[1])

markers = ['+','*','.','d','^','v','>','<','p']

# plotting the cluster
i = 0
# print(cluster_list)
for value in cluster_list:
    cluster = cluster_list[value]
    plt.plot(cluster[0],cluster[1],markers[i])
    i = i%8+1

#plot the noise points as well  
noise_points=[]  

for point in all_points:
    if not point in core_points and not point in border_points:
        noise_points.append(point)  

noisex=[]  
noisey=[]  
for point in noise_points:
    noisex.append(point[0])  
    noisey.append(point[1])
plt.plot(noisex, noisey, "x")  

plt.axis((50,100,0,160))  
plt.show()

调参看看结果吧，反正我的结果有点惨不忍睹。

自己实现的和官方的差距还是很大的，与现实预期相差甚远啊。

参考文献

1. wikipedia DBSCAN
2. 简单易学的机器学习算法——基于密度的聚类算法DBSCAN
3. A Density-Based Algorithm for Discovering Clusters
   in Large Spatial Databases with Noise
4. 正态分布（Normal distribution）又名高斯分布（Gaussian distribution）