矩阵与线性变换

矩阵与线性变换

矩阵变换

Think about a matrix multiplication as a transformation of space.

对 Rn 中的每个向量 x ， T(x) 由 Ax 计算得到，其中 A 是 m×n 矩阵，将这样一个矩阵变换记为 x→Ax 。

显然 T 的值域为 A 的列向量的所有线性组合的集合。

线性无关：

一组向量中的任何一个向量都很“独立”，不能用这组向量中除他之外的任何其他向量的任何线性组合来表示。

线性相关：

一组向量中只有部分向量是“独立”的，他们代表了整个向量组的维度(秩)，因为组内的任何其他向量都可以由这些独立的向量的某种线性组合来表示。

线性组合：

如果向量 b 可以表示为一组向量 a1,a2,a3,...,an 的系数乘和，即 b=x1∗a1+x2∗a2+x3∗a3+...+xn∗an ，则称 b 向量是向量组 a1,a2,a3,...,an 的一个线性组合。

线性变换

线性变换是线性代数中最重要的一类变换。

定义：

变换（或映射） T 称为线性变换的，若：

• 对定义域内的一切 u,v ， T(u+v)=T(u)+T(v) 。
• 对定义域内的一切 u ； 和任何标量c， T( c u)= c T(u) 。

可以证明，每一个矩阵变换都是线性变换，反正则不成立。

意义

知道矩阵变换是线性变换有什么好处呢？能够简化向量转换的计算过程吗？能够方便我们理解向量变换吗？

看下面的例子：

二维向量空间的单位正交基可以用单位矩阵 I=[1001]=(e1,e2) 表示，设 T 是一个 R2→R3 的矩阵变换，有：
T(e1)=⎡⎣⎢5−72⎤⎦⎥ ， T(e1)=⎡⎣⎢−380⎤⎦⎥

求 R2 中的任意一个向量 x=[x1x2] 被 T 变换后的向量。

解：

二维向量空间 R2 中的任何一个向量都是基向量 e1,e2 的某个线性组合：

x=[x1x2]=x1e1+x2e2

因为我们知道矩阵变换是线性变换，由线性变换我们可以得出：

T(x)=T(x1e1+x2e2)=T(x1e1)+T(x2e2)=x1T(e1)+x2T(e2)=[T(e1)T(e2)][x1x2] 。

T(e1),T(e2) 已知，所以结果就很容易得出了。

可以看到，对任何向量 x 进行线性变换 T 的结果向量，是一个对基向量组进行线性变换 T 之后的新向量组的一个线性组合，系数没变。看下面的图示，一目了然：

上图是某个线性变换之前，黄色向量与绿色基向量和红色基向量之间的关系。

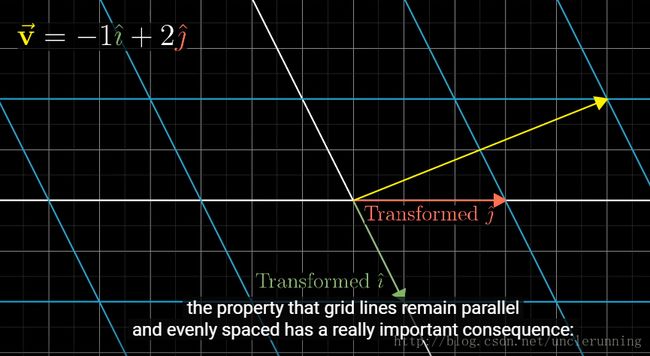
可以看到，线性变换之后，平行关系保持，原点位置不变。

正如前面所说，变换之后，新的 v 向量是变换之后的新的基向量的线性组合，组合系数没有改变。

这个性质给了我们能力：

只需要知道两个基向量（ i 向量和 j 向量）转换之后的的结果，而不用知道转换本身，我们就能推导出二维空间中所有向量转换之后的结果。

向量旋转变换

OpenGL中经常会使用的平移矩阵、缩放矩阵以及旋转矩阵。其实前两种矩阵很好理解，引入齐次坐标系非常直观地就能写出一个平移矩阵（当然平移变换不是线性变换），对单位矩阵的对角线上的值进行设置就能非常直观地表示沿着对应坐标轴的缩放。然而，沿着某个坐标轴旋转的旋转矩阵却不怎么直观，不像前两种矩阵这么好理解。不过，有了矩阵变换是一个线性变换的知识，我们其实可以比较直观的表示一个沿坐标轴旋转的旋转矩阵。

对于不是沿坐标轴旋转的变换，都可以通过坐标系变换，转换成沿“坐标轴旋转”。旋转之后，再变换回原坐标系。

从上面的例子，我们得出结论：

只要知道矩阵变换 T 作用于基向量组的结果，我们就能用一个矩阵来表示这个矩阵变换。

设 T(m) 是一个将三维向量 m=⎡⎣⎢xyz⎤⎦⎥ 沿 x 轴顺时针旋转 θ 度的变换 T(m)=Am ，求这个变换矩阵 A 。

T(m)=T(xe1+ye2+ze3)=T(xe1)+T(ye2)+T(ze3)=xT(e1)+yT(e2)+zT(e3)=[T(e1)T(e2)T(e3)]⎡⎣⎢xyz⎤⎦⎥

所以， A=[T(e1)T(e2)T(e3)] ， 对基向量进行变换，很直观的就能得到这个旋转矩阵：

A=⎡⎣⎢1000cosθ−sinθ0sinθcosθ⎤⎦⎥

齐次坐标形式为：

A=⎡⎣⎢⎢⎢10000cosθ−sinθ00sinθcosθ00001⎤⎦⎥⎥⎥

同理可以很容易的推出沿其他轴旋转的旋转矩阵。

拓展

“Mathematics is the art of giving the same name to different things.” -Henri Poincare

我们说一个三维空间中的点 P 的坐标是 (x,y,z) ，意味着，向量 OP=x∗i⃗ +y∗j⃗ +z∗z⃗  ，其中， i⃗ ,j⃗ ,z⃗  是 P 当前坐标系的基向量。如果 i⃗ =(1,0,0),j⃗ =(0,1,0),z⃗ =(0,0,1) ，那么，坐标是 (x,y,z) 是点 P 在标准世界坐标系中的一个坐标。

实际上， i⃗ ,j⃗ ,z⃗  不一定非得是前面所说的标准单位正交基，三维空间中的基向量组可以由任何不共线且不共面的（线性无关）三个向量组成，这样任意的 i⃗ ,j⃗ ,z⃗  组成的坐标系和标准世界坐标系共原点，不同的地方就是坐标轴的夹角（方向）和单位长度发生了改变。

对于这样推广之后的坐标系统，前面提到的性质保持，即：

只要知道矩阵变换 T 作用于基向量组的结果，我们就能用一个矩阵来表示这个矩阵变换。

直观上说，矩阵变换会切换坐标系，但是不会改变坐标。矩阵变换的结果是一个位于标准世界坐标系中的向量，或者点。明白这点很重要，尤其在坐标系变换中：

⎡⎣⎢x′y′z′⎤⎦⎥ = A⎡⎣⎢xyz⎤⎦⎥ ⇒ ⎡⎣⎢xyz⎤⎦⎥ = A−1⎡⎣⎢x′y′z′⎤⎦⎥

当然，如果你明白我的意思：坐标是相对于坐标系的。

例如，原来的坐标系 Ori 的基向量组是 a⃗ ,b⃗ ,c⃗  ，点 P 在 Ori 中的坐标为 (x,y,z) ，或者， O 为坐标原点，你可以说向量 OP=x∗a⃗ +y∗b⃗ +z∗c⃗  。 Ori 的基向量经过线性变换 T 之后变成了 r⃗ ,s⃗ ,t⃗  ，那么点 P 转换之后的点 P′ 在以 r⃗ ,s⃗ ,t⃗  为基向量组的坐标系 Trans 中的坐标仍然是 (x,y,z) ，或者，你可以说向量 OP′=x∗r⃗ +y∗s⃗ +z∗t⃗  。

进一步地，我们可以认为，连续作用地线性变换的组合的效果就是：

坐标系数不变，连续地切换坐标系。

我特意强调“坐标系数不变”是因为：

相对于标准世界坐标系，这些变化确实在不断地改变一个点的坐标。但是，相对于变换过程中的的各个坐标系，如果坐标点在变换之前的坐标系中的坐标是 (x,y,z) ，那么，在变换之后的坐标系中，该点的坐标仍然是 (x,y,z) 。

所以，这里的重点是：

说到一个点的坐标时，永远伴随着一个特定的坐标系。

总结

所以下次你看到一个矩阵 A 时，当然不包括齐次坐标系下的平移矩阵，你可以把它看成一个线程变换 T 。 A 的每一列 x 都是一个标准单位正交基向量 ex 经过 T 变换之后的结果，任何一个向量 v ，经过 T 变换之后的结果为 Av 。

references

Transformations

YouTube-Linear transformations and matrices

YouTube-Change of basis