深度学习基础入门

课程简介

本课程共分为三个部分：基础理论、深度神经网络基本结构以及网络优化与实践。本课程采用了理论结合实践的讲解方式，方便读者边学边练，理解巩固。在解释相关概念时，作者尽力使用简单、直观、可实现的公式语言描述，尽量避免使用图形、比喻和白话等容易使初学者误入歧途的描述方式。读者在初学过程中可能会不太习惯，但这对于建立知识体系是十分重要的。

课程实践部分使用 TensorFlow 作为机器学习库，以帮助读者快速实现一些深度学习算法，从而建立信心，这种自信是任何学习过程都需要的。但机器学习库只是辅助，作者希望读者在学完本课程后，能够利用数学公式而非库函数的方式实现深度学习功能。这很难，但并不是不可能。

作者介绍

如是，算法工程师。主要从事数值模拟、智能算法研发工作。擅长高性能计算、物理、机器学习领域。曾参与设计自然灾害智能监控预报系统。

课程内容

导读：课程介绍和学习方法

无人工不智能

经常会被问到“深度学习与机器学习或者数据挖掘有什么关系？”答案很简单：没有区别。现如今，人工智能如此火爆，好像其他机器学习算法已经没有了立足之地。但事实并非如此，每一种机器学习算法都具备完成所有机器学习任务的潜力，只是需要很复杂的特征工程。深度学习以及其他所有的机器学习算法本质上都是一种“拟合”机制，在大量的数据基础之上总结出可用的规律。而这些数据是需要人来提供的，所以说机器学习过程就是让机器学习人类经验的过程。而这个过程与数据有关，与方法无关。

解决深度学习问题有两种思路。一种思路是基于理论的，或者说基于规则；第二种是基于数据的，从数据中学习规则。举个例子，对于图像去噪问题。我们可以通过傅里叶变换与低通滤波来减少图形噪声，这是基于理论的而且不需要提供数据。另外，还可以给定有噪声和没有噪声的图像，让机器自动去学习一个可用于降噪的系统。下图是Zhang在2017年使用深度神经网络完成的图像去噪工作（文献[1]）。

所有的机器学习都依赖于有效数据的累积，这离不开人工。“无人工不智能”的另外一层意思是很多工作其实并不适合使用“机器学习算法”去完成，比如寻找两点之间的最短路径，这是传统算法的范畴。作为一个“算法”工程师，眼光不应该局限于机器学习的领域。我们最终的目标是准确、高效地解决问题，因而不必纠结于使用哪种方法。

为什么需要深度学习

很多年前机器学习很强调“做特征”。但是随着数据的不断累积，有了另外一种选择，就是构建一个足够复杂的可训练系统，让系统自身去完成特征的学习过程。深度学习就可以完成上述过程，它简化了特征工程的难度。

传统的机器学习建模方式所得的曲面（线）复杂度不足，无法用来拟合数据。

传统机器学习算法由于可训练参数数量的限制，导致它所能学到的特征有限，在一些情况下可能无法形成足够复杂的曲面，因此它十分依赖特征工程去增加复杂度。而深度学习可以形成足够复杂的曲面用于拟合特征，换一种说法就是深度神经网络具有强大的表达能力。这种特征的习得是以海量数据为基础的。因此在数据量较少时使用深度学习很难得到理想的结果。

深度学习能做什么

机器学习能完成的任务，深度学习都可以完成。深度学习尤其擅长处理图像识别、物体检测、自然语言翻译、语音识别和趋势预测等，这些任务本身比较复杂，需要一个相对复杂的系统去完成拟合任务，在这里就不展示了。下面列举深度学习在其他方面的应用：

谷歌的 Magenta 项目是深度学习在音乐以及艺术上的一些探索。目前利用深度学习已经完成了一些简单的音乐和漫画创造工作。下面是 Magenta 项目中画漫画的例子：

深度神经网络还可以完成图像风格迁移的任务：

同样，使用神经网络可以完成图像的超分辨率采样等任务：

上图是利用 Keras-js 官网的预训练模型进行超分辨采样，左侧是使用二次样条插值得到的图像，右侧是使用神经网络得到的图片。不难看出，深度神经网络在进行超分辨采样的过程中可以保留更多细节。

如何学习

歧途之上的零基础

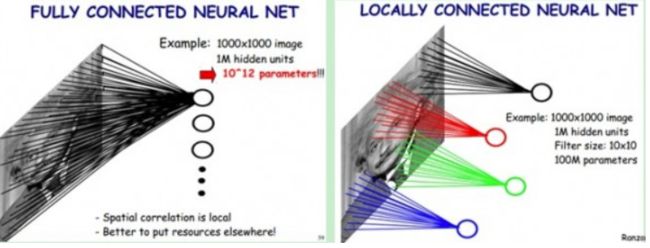
“零基础入门”很多，一些机器学习课程也喜欢用这种诱人的名字。这是十分不负责任的做法。任何一门学科的学习，都需要付出时间和精力，更何况是涉及很多理论知识的机器学习。如果通过图形和比喻来介绍机器学习，那大概只能算是科普。比如，很多零基础入门课都喜欢用下面这样的图：

卷积神经网络本身只需要一个公式就可以很好地描述了，简单明了而且可直接用程序实现。但上面这张图不仅未解释任何问题，反倒增加了学习者的困惑。学习者以为了解了卷积网络，实践时却发现只是冰山一角。科普很久还需要从头学起，不但没有走捷径反而浪费了时间。

学习本身并不难

深度学习作为一门学科，需要一定的基础，要想掌握它也需要投入一些时间，但它并没有你想象得那样难以掌握。如果以实现为导向的话，仅需要熟悉一些矩阵、导数的知识就可以完成深度学习的网络搭建工作了。这里的搭建指的是不借助任何机器学习库完成的深度学习的网络搭建。这样一来，学习周期自然会比较长，学习过程中也会遇到一些障碍，但并不是难以逾越的。

下面是我在学习过程中总结出的一些难点：

• 多维函数和优化
• 概率论
• 深度学习中的贪心与动态规划思想

从函数角度来看，深度学习是一个多维函数的问题。多维函数使用过程中涉及了矩阵（张量）相关计算，是程序实现过程中的难点。概率论相关内容一直是机器学习中最难以理解的部分，但它是基础，必须要掌握。贪心算法是深度学习中最基本的思想之一，它植根于每个实现过程中。有的时候你甚至都没意识到那是一种贪心策略，最明显的例子就是“梯度下降法”。克服上述障碍之后就可以完整地实现深度神经网络了。

系统的学习方法

对于深度学习而言，需要系统学习的内容包括：

• 矩阵与函数
• 最优化理论
• 概率与统计

其他补充知识包括但不限于：

• 现代几何
• 流形
• 传统算法
• 高性能计算

学习过程中尽量以公式角度来理解和看待问题，进而形成一种自洽的理解方式，这是非常重要的。尽量避免使用图形理解与分析问题，因为那样更像是科普而不是学习。

软件环境

本课程使用的软件环境是 Python 3版本，这里推荐安装 Anaconda 最新版本。包含了学习过程中必须的库：

• numpy
• scipy
• matplotlib

TensorFlow 需要自行安装，这里推荐使用最新版本。如果不熟悉 Python 环境，那么推荐的安装方式为：

pip install tensorflow

如果有英伟达的 GPU 的话，可以安装 GPU 版本：

pip install tensorflow-gpu

这种安装方式的一个缺陷在于，库函数没有使用 CPU 的 SIMD 指令集进行优化，因此自己编译成了更好的选择，这个过程可以参考官方文档。

课程结构

本课程分为三个部分：

• 基础理论
• 深度神经网络基本结构
• 网络优化与实践

基础理论包括：

• 线性代数与矩阵
• 多维函数与优化
• 概率与概率模型
• 神经网络建模与优化

深度神经网络基本结构包括：

• 卷积神经网络
• 循环神经网络
• 循环神经网络结构与文本损失函数

优化与实践包括：

• 网络参数优化
• 网络模型优化
• 图片识别器
• 语音生成器

希望通过本课程的学习，读者能够对深度神经网络有一个具体而微的了解，甚至可以在不借助任何机器学习库的情况下直接编程实现。这很难，但并不是不可能。

参考文献

[1]Zhang K, Zuo W, Chen Y, et al. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2017, 26(7):3142-3155.

第01课：线性代数

矩阵与符号

矩阵是深度学习中最基本的概念之一，深度学习的建模以及优化实现都是围绕矩阵进行的。矩阵概念映射到计算机科学中就是数组：

${A}{mn}=\begin{bmatrix}a{11}&\cdots&a{1n}\\vdots&\ddots&\vdots\a{m1}&\cdots&a_{mn}\end{bmatrix}\in \mathbb{R}^{m\times n}$(1.1)

1.1式中 $\mathbb{R}^{m\times n}$ 代表矩阵为 m 行 n 列的实数矩阵。矩阵可以写为 ${A}$ 或 $[a_{ij}]$。对于我们所接触的机器学习问题而言，矩阵内的数值通常为实数。

约定求和

矩阵的点乘、向量内积可以用约定求和来表示：

$(A{mn}\cdot B{np}){ij}=\sum{i=1}^n a{ik}b{kj}\rightarrow a{ik}b{kj}$(1.2)

相同指标 k 代表求和，此时可以省略求和符号。相似的向量相乘可以表示为：

$\vec{a}\cdot \vec{b}=aibi$

约定求和是公式推导过程中非常方便的工具，可以简化公式的书写。

矩阵分解

一个向量可以分解成多个向量相加的形式：

$\vec{v}=a1 \vec{e1}+\cdots+an \vec{en}$(1.3)

对于一组不全为0的向量而言，如果其中的任意一个向量都不能由其他向量以1.3式的方式表示，那就代表这组向量线性无关或这组向量是线性独立的。

线性独立的概念很重要。如果几个向量线性不独立，即某个向量可以用其他向量表示，那么这个向量就没有存储的必要了。这是信息压缩最原始的思想。如果对1.3式中等式右边向量 $\vec{e}$ 加以如下正交约束：

$\vec{e}i\cdot \vec{e}j=\delta_{ij}$(1.4)

1.4式中所描述的向量之间是互相正交的关系，并且是单位向量：

$\delta_{ij}={\begin{matrix}1&i=j\0&i\neq j\end{matrix}$(1.5)

那么 e 就组成了 n 个正交的单位基向量。这是在空间中所用到的概念。当然并不是所有坐标基向量都是正交的，同样也未必是单位向量。

压缩概念初探

对于一组向量 $V=(v1,\cdots,vm)$ 来说，可以将其中每个向量都用其他多个向量以加权求和的方式表示：

$v{ki} = a{kj} e_{ji}$(1.6)

其中 $e{ji}\rightarrow(\vec{e}j)i$ 代表第 j 个单位向量的第 i 个元素。同样， $v{ki}$ 代表第 k 个向量的第 i 个元素。由1.2式可以看出，上式可以表示为矩阵相乘的形式：

$V{mn}=A{mk}\cdot E_{km}$(1.7)

1.7式中向量 v 组成的矩阵 V 可以分解为两个矩阵 A、E 的乘积表示。如果 m>k，也就是说我们可以用小于 m 个数字来表示矩阵 V，这是一个数据压缩过程。此时 A 可以代表矩阵 V 的特征，如果要恢复 V 的话还需要保存 E。但是机器学习中通常只需 A 就可以了。

从这里例子中可以看到，我们可以对矩阵进行变换，从而达到信息压缩的目的。这个过程中需要的是求解矩阵 E。如果 $W=E^T$，则信息压缩方式可以写为：

$V{mn}\cdot W{nq}=A_{mq};n

W 称为变换矩阵。这是线性变换过程。

第一种线性变换：特征值分解

特征值分解是最简单的一种矩阵分解形式，也是矩阵算法中最常用的。特征值分解是对于方阵而言的：

$A_{nn}=E\cdot\Lambda \cdot E^{-1}$(1.9)

特征值分解中 E 矩阵是正交矩阵，这意味着：

$E^{-1}=E^T$(1.10)

此时，1.8式中的变换矩阵 W 即为 $E$。

第二种线性变换：奇异值分解

特征值分解作为矩阵的分解方法，最主要的缺点在于它只能应用于方阵。对于非方阵情况下的矩阵分解算法，比较有代表性的就是奇异值分解（SVD）：

$A_{mn}=M\cdot\Gamma \cdot V$(1.11)

SVD 的求解过程可以用特征值分解进行，这就需要将矩阵转换为方阵：

$B_{nn}=A^T\cdot A=E\cdot \Lambda\cdot E^T$(1.12)

对 B 进行特征值分解，利用对应元素相等可以得到如下关系：

$\begin{matrix}V=E^T\\Gamma=\sqrt{\Lambda}\end{matrix}$(1.13)

根据1.11式可以得到 M 为：

$M=A\cdot V^T \cdot \Gamma^{-1}$(1.14)

由此三个矩阵已经完全确定，因此可见矩阵的特征值分解是 SVD 的基础（还有其他算法可以实现）。同时可以看到，矩阵 A 在变换为矩阵 M 的过程中，依然相当于对矩阵 A 进行的一次线性变换。

第三种线性变换：字典学习

对于 SVD 分解而言，其有一个非常大的问题就是约束过于严格，比如矩阵 M 与 V 为正交矩阵。这就导致了在计算过程中，为了满足分解条件，信息压缩的质量可能会降低。因此产生了另外一个更加宽泛的约束方式：

$A{mn}\approx M{np}\cdot N_{pm}$(1.15)

假设条件是 N 足够稀疏，此时 M 就称为字典。此时弱化了正交性假设，因此所得到的信息压缩效果会更加出色。

实践部分

矩阵定义与计算

在 Tensorflow 中最简单的矩阵乘法运算可以写成如下形式：

#矩阵乘法#引入库import tensorflow as tfimport numpy as np#定义常量并用 numpy 进行初始化a1 = tf.constant(np.ones([4, 4]))a2 = tf.constant(np.ones([4, 4]))#矩阵乘法a1_dot_a2 = tf.matmul(a1, a2)#定义会话用于执行计算sess = tf.Session()#执行并输出print(sess.run(a1_dot_a2))

这是通过常量进行定义的，一般的函数库是按顺序执行的，比如 numpy 中。而 tensorflow 在运行过程中，我们一直都只是在描述计算，直到定义了会话并运行之后才真正开始计算。这样一来，就可以用较慢的 Python 来描绘计算过程，而需要快速计算时，利用会话（session）可以实现 Python 所描述的计算。

Python 中用得最多的是变量：

#矩阵乘法#引入库import tensorflow as tfimport numpy as np#定义变量并用 numpy 进行初始化a1 = tf.Variable(np.ones([4, 4]))a2 = tf.Variable(np.ones([4, 4]))#矩阵乘法a1_dot_a2 = tf.matmul(a1, a2)#variable 需要初始化init = tf.global_variables_initializer()sess = tf.Session()sess.run(init)print(sess.run(a1_dot_a2))

变量是在计算过程中可以不断变化调整的量，是可求导的量，这对于机器学习来说是比较重要的，后面会提到。这里需要注意的是用到变量时需要对变量进行初始化，否则会出错。

上面说到我们用 Python 来描绘计算过程，称为计算图。在描述之后，很难对变量进行外部输入。因此这里引入了 placeholder，用于从外部接收数据：

#矩阵乘法#引入库import tensorflow as tfimport numpy as np#定义变量并用 numpy 进行初始化a1 = tf.Variable(np.ones([4, 4]))#定义 placeholder 用于从外部接收数据a2 = tf.placeholder(dtype=tf.float64, shape=[4, 4])#矩阵乘法a1_dot_a2 = tf.matmul(a1, a2)#variable 需要初始化init = tf.global_variables_initializer()sess = tf.Session()sess.run(init)# 需要给 placeholder 提供数据print(sess.run(a1_dot_a2, feed_dict={a2:np.ones([4,4])}))

想象一下，我们在运行过程中只需不断地从外部输入 c2，就可以持续地获取输出 a1_dot_a2，这个过程对于机器学习输入样本来说，非常简便。

小提示：注意格式检查，在计算过程中，float 64 与 float 32 放在一起使用会产生错误。

[help me with Html]

第02课：多元函数和优化

第03课：概率问题

第04课：基础数学概念扩展

第05课：库函数的补充

第06课：卷积神经网络

第07课：循环神经网络（上）

第08课：循环神经网络（下）

第09课：神经网络辅助结构

第10课：网络优化

第11课：神经网络模型实践：图片分类器

第12课：神经网络模型实践：图片分类器修改

阅读全文: http://gitbook.cn/gitchat/column/5b1e313c294fb04d7c22b3d1