数据结构(严蔚敏版)
注重搞清楚基础概念,为笔试做准备
第一章:绪论,基本概念
数据结构在计算机中的表示,成为存储结构。其中最小的单位是位。
一般分为两种表示方法,对应两种存储结构:顺序结构与链式结构
数据类型:一个值的集合以及定义在这个集合的值的一组操作
时间复杂度:常量复杂度,线性O(n),平方,指数,对数等
第二章:线性表-vector(顺序存储结构、线性表)-list(链式存储结构、线性链表)
特点:1、有唯一的“开头”“结尾” 2、除了开头,其他元素都有唯一的“前驱” 3、除了结尾,都有唯一的后继
线性表特点:两元素的存储位置物理相邻,因此可以随机存取
线性链表特点:使用指针连接,分布存储。不能随机存取,但方便插入数据
head头结点为连接在第一个节点之前的一个不存储数据的节点。首节点指第一个节点
循环链表 特点:表尾元素指针指向表头元素
第三章:栈与队列
栈和队列从数据结构的角度也是线性表(也可按存储结构分为顺序栈和链栈),他们是线性表操作的子集
栈:仅限定在表尾进行插入和删除操作的线性表。表尾就是栈顶
原理、原则:后进先出
栈与函数与递归:系统调用函数需要做三件事1、保存参数和返回地址等 2、为函数开辟存储空间 3、将控制专业到函数入口
当有多个函数嵌套调用时,根据“后调用先返回”原则,系统在栈顶开辟临时存储空间供函数内部临时变量使用。内存中分为5个区域 1、栈 2、堆 3、全局 4、常量 5、代码。函数中的临时变量存储于栈区,而使用new和mallow开辟的空间存储于堆区。 递归就是特殊的函数调用,自己调用自己。临时变量和数据的保存也是利用栈的特性实现。
栈区的大小由操作系统管理,一旦使用递归太深,导致栈空间不够,就会栈溢出(stack overflow)。
队列:仅限定在表尾进行插入和限定在表头进行删除操作的线性表。(分为顺序列队和链列队)
原理、原则:先进先出
第四章:串
串与线性表一样,使用连续地址的存储空间来存储串(也有用链式结构的,貌似比较少吧)
第六章:树与二叉树
一个节点的子树数目,成为节点的度。度为0的节点为叶子或终端节点。
根节点为第一层,树中节点的最大层数称为树的深度。
二叉树 特点:每个节点最多只有两棵子树,且子树有左右之分不能颠倒
满二叉树:k层有2^k-1个节点。 完全二叉树:如有n个节点,则节点与满二叉树的1到n号节点一一对应。
存储结构:1、顺序存储(使用数组,占满二叉树的空间)
由上图片顺序可知,根节点序号为1,从左往右从上往下递增。儿子/2为父节点序号。如父节节点序号为i,左儿子为2i,有儿子为2i+1.如根节点为0情况自行推导。
2、链式存储(使用指针指向子节点,节省空间,但访问父节点必须从根节点重新寻找)
二叉树遍历:前序-根左右 中序-左根右 后序-左右根
只有知道中序+先或后续才能确定一棵二叉树,只知先后遍历不能确定。
二叉查找树的中序遍历结果是升序序列
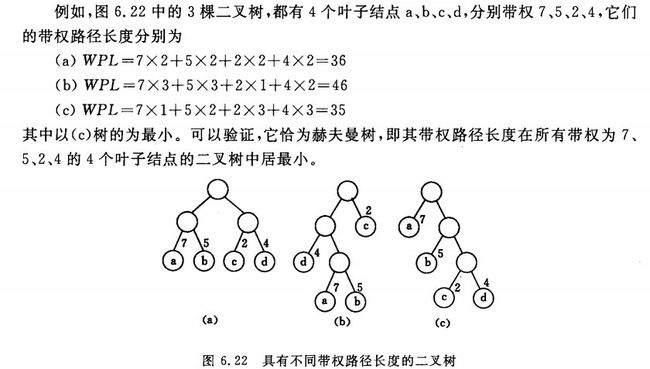
哈佛曼树:最优二叉树,所有结点的深度与权重乘积之和最少的树。
如图,经过huffman算法得到的最优树如c 图,WPL最小。 哈夫曼树的思想其实就是把权重大的节点放得靠近根节点,使其层数尽量少,因此更快地解决,而权重小的节点可以适当放下点。
哈佛曼算法:1、选权重最小的两个节a,b点作为新节点c的儿子,新节点权重为两节点之和。2、未处理节点集中删除a,b 3、未处理中放入c。 重复直至未处理集中没有节点。
第七章:图
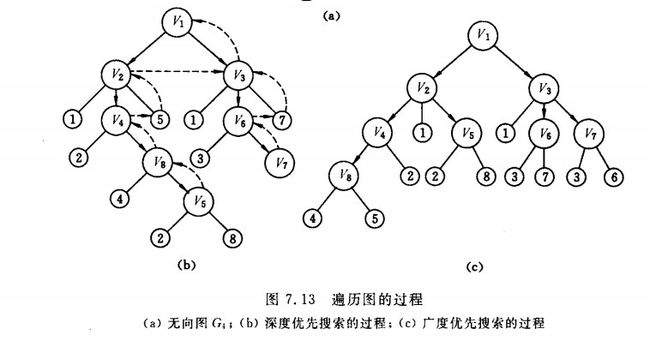
深度优先图搜索:从一个当前节点出发,优先访问当前节点的邻节点,然后将此邻节点设为当前节点,继续访问其邻接点,直至没有邻接点位置。此时,再选择一个标记为未访问的节点重新开始深度优先搜索。
广度优先图搜索:从一个当前节点出发,优先访问当前节点的所有邻接点,然后分别再从各个邻节点出发进行广度优先访问。类似于二叉树遍历。
(b)v1-v2-v4-v8-v5 没有了 跳到v3-v6-v7 (c)v1-v2-v3-v4-v5-v6-v7-v8
第九章:查找
查找表使用关键字(key)索引,如果一个关键之可以唯一标识一个元素,则是primary key。
1、静态查找:只有判断某元素是否存在,或者读取某元素的操作
查找表的性能 平均查找长度来衡量:找到被查找值所需要对比次数的期望值
顺序查找:适用性广(顺序、链式结构都可以),但数量大时查找速度慢。
折半查找:适用于有序表,并且只适用于顺序存储结构的表。
索引顺序表(分块查找)1、查找所在的块 2、块中查找
2、动态查找: 特点:如被查找的元素存在则返回成功,否则插入该元素
包括:二叉查找树,AVL树,B树,B+树,红黑树等。。
动态查找表的实现结构
(1)二叉排序树(二叉查找树):左小于根,右大于根,它的子树也是二叉查找树。
查找或插入:从根节点不断往下对比,直到最后一个节点,如叶节点是要找元素则成功,否则新建节点插入。
(2)平衡二叉树查找树(AVL树):左右子树都是AVL数,且深度相差不超过1。 它也是查找树。
当某些极端情况时(数据严格排序),二叉查找树的查找效率可能会退化到O(n)(就是所有元素都放在同一个方向的叉的情况)。而构造平衡二叉树则可保证查找效率为log2n。
http://www.cppblog.com/cxiaojia/archive/2012/08/20/187776.html
AVL树构造:如平衡因子大于|1|,则对子树进行左旋或者右旋处理,使所有子树归于同一个叉,再以中间的元素作子树根节点,构造13,24,37,93,53,如图所示
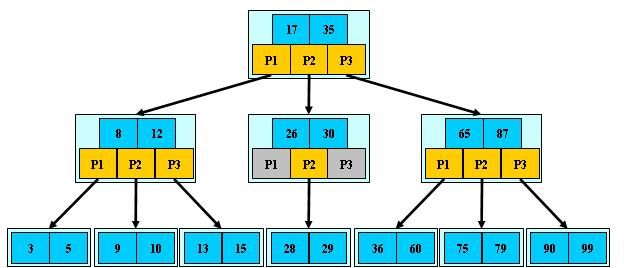
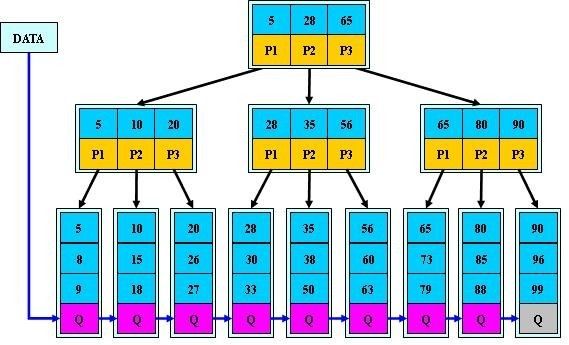
(3)B-查找树(B-树跟B树是同一个东西)
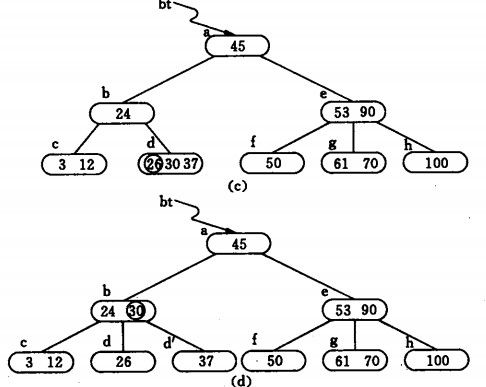
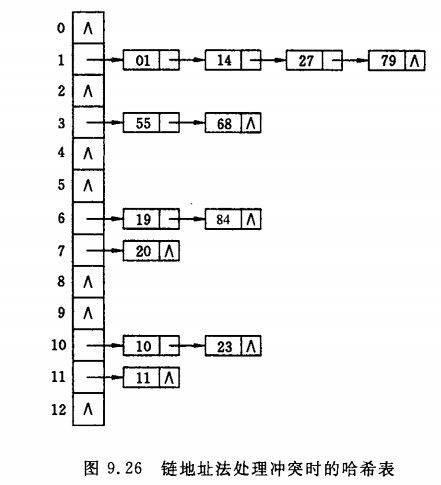
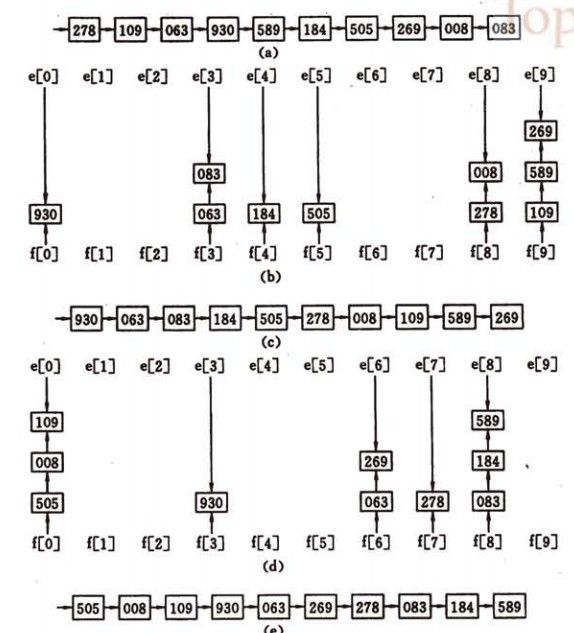
1、关键字Ki 2、A0所指子树的所有关键字均小于K1,An指针所指子树关键字均大于Kn,其余指针指向大于ki且小于ki+1的子树。 根据B-树的特性,查找方法是显而易见的。(到了子树内部可以用折半查找) B-树的插入:m阶树的节点关键字数不能超过m-1.如关键字数没超过则直接插入,否则分裂。分裂如下图 B-树的删除:删除后应检查是否需要合并节点。 (4)B+树:一棵m阶的B+树和m阶的B树的异同点在于: 1.有n棵子树的结点中含有n-1 个关键字; (与B 树n棵子树有n-1个关键字 保持一致) B+树的插入、删除与查找与B树差不多,差别是就算非叶节点值等于查找值,也需要继续往下查找直到叶节点。 B树、B+数的使用背景: 但是咱们有面对这样一个实际问题:就是大规模数据存储中,实现索引查询这样一个实际背景下,树节点存储的元素数量是有限的(如果元素数量非常多的话,查找就退化成节点内部的线性查找了),这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下,那么如何减少树的深度(当然是不能减少查询的数据量),一个基本的想法就是:采用多叉树结构(由于树节点元素数量是有限的,自然该节点的子树数量也就是有限的)。 也就是说,数据都是存储在外部存储器,如像二叉树结构的话,每次对比都要读取一次外部存储器,导致查询效率低下。减少读取次数首先想到的是降低树的深度,从而想到了B-Tree,但其本质还是和二叉树差不多还是每次比较都要读取(因为其非叶节点也是有效数据)。为了解决这个问题,B+tree出场。他的非叶节点只是索引(用作比较)而已,所有的数据都在最底层的叶子节点。因此可以把B+树的非叶节点全部建立在内存之中,直到最后找到叶子节点才跳至外部存储器中,从而大大降低访问外存的次数,提高效率。 哈希表 哈希表构造方法:1、直接法(key刚好对应连续内存情况)2、平方法(key平方后取几位)3、折叠法(把key分成几个部分,取各部叠加为地址)4、余数法(除数一般选20以下质数) 冲突:计算出来H(key)地址上已有值,则再进行计算,直到找到空地址。 处理冲突方法:0、开放地址法:算出来冲突了,地址直接加1,直到不冲突为止 1、线性地址法((H(key)+d)mod m)2、再哈希法(遇到冲突后再算另外一个哈希函数)3、链地址法(如下图) hash记录分组存储,若干个记录组成的一个存储单位称为 桶(hash桶)。 文件索引 三种索引方式:1、顺序索引 2、直接索引 3、关键字索引 第十章:内部排序 稳定性:弱排序前后两相同元素的前后关系不变,则称排序方法是稳定的。 内部排序:排序记录全部存放于内存中的排序 外部排序:记录数量太大,需要分几次读取外存进行排序 插入排序 稳定 O(n^2) 选择排序 不稳定 O(n^2)选择a[i+1,n]中最小的数作为a[i] 堆排序 不稳定 O(nlogn)父节点一定大于(小于)子节点的二叉树成为最大(最小)堆。通过不断删除堆顶元素排序 归并排序 稳定 O(nlogn)递归合并两有序数组(链表存储结构的话用归并比较快,因为快排需要随机存取) 基数排序(多关键字排序)稳定 O(kn)k为元素所含关键字最大数目 通过逐次按关键字分配,再收集排序,如下图 第十一章:外部排序 外部排序是指待排序的记录存放在外部存储器中,排序过程中需要多次的内、外存之间交换数据。外部存储器的时间主要消耗在磁盘的寻查时间上,因此应尽量将数据存储在同一或相邻柱面的磁盘区域中。外排的基本方法是归并。 对m个初始归并段进行k路归并,归并次数s=logkM,增加k减小m可减少s,减少访问外存的次数。
2.所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
3.所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。 (而B 树的非终节点也包含需要查找的有效信息)
4.有两个头指针,一个指向root,一个指向最小的叶节点数据,用于遍历所有数据。
也就是说,因为磁盘的操作费时费资源,如果过于频繁的多次查找势必效率低下。那么如何提高效率,即如何避免磁盘过于频繁的多次查找呢?根据磁盘查找存取的次数往往由树的高度所决定,所以,只要我们通过某种较好的树结构减少树的结构尽量减少树的高度,那么是不是便能有效减少磁盘查找存取的次数呢?那这种有效的树结构是一种怎样的树呢?
这样我们就提出了一个新的查找树结构——多路查找树。根据平衡二叉树的启发,自然就想到平衡多路查找树结构B-tree,B树的各种操作能使B树保持较低的高度,从而达到有效避免磁盘过于频繁的查找存取操作,从而有效提高查找效率。
希尔排序shell sort(分段的插入排序) 复杂度未知 不稳定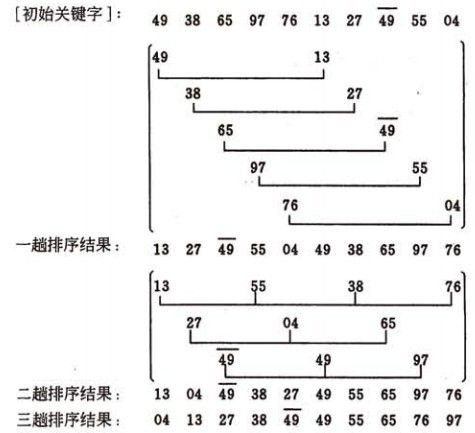
冒泡排序 稳定 O(n^2)
快速排序 不稳定 O(nlogn) 记录下r[0]作为pivot,然后r[0]作为第一个被覆盖的位置,采取这种覆盖的策略来避免交换数组元素,提高效率。
记录下r[0]作为pivot,然后r[0]作为第一个被覆盖的位置,采取这种覆盖的策略来避免交换数组元素,提高效率。