论文:Towards End-to-End Lane Detection: an Instance Segmentation Approach
代码:https://github.com/MaybeShewill-CV/lanenet-lane-detection
参考:车道线检测算法LaneNet + H-Net(论文解读)
数据集:Tusimple
Overview
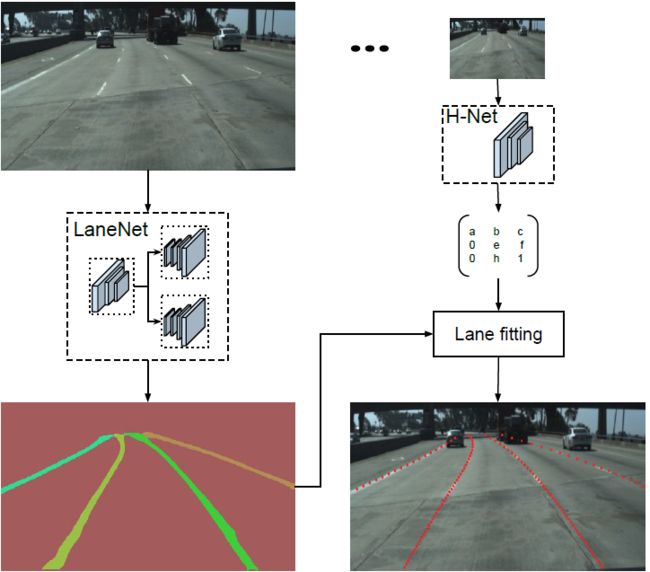
本文提出一种端到端的车道线检测算法,包含 LanNet + H-Net 两个网络模型。其中 LanNet 是一种将语义分割和对像素进行向量表示结合起来的多任务模型,最后利用聚类完成对车道线的实例分割。H-Net 是有个小的网络结构,负责预测变换矩阵 H,使用转换矩阵 H 对同属一条车道线的所有像素点进行重新建模(使用 y 坐标来表示 x 坐标)。
LaneNet
论文中将实例分割任务拆解成语义分割(LanNet 一个分支)和聚类(LanNet一个分支提取 embedding express, Mean-Shift 聚类)两部分。如上图所示,LanNet 有两个分支任务,分别为 a lane segmentation branch and a lane embedding branch。Segmentation branch负责对输入图像进行语义分割(对像素进行二分类,判断像素属于车道线还是背景);Embedding branch对像素进行嵌入式表示,训练得到的embedding向量用于聚类。最后将两个分支的结果进行结合利用 Mean-Shift 算法进行聚类,得到实例分割的结果。
语义分割
在设计语义分割模型时,论文主要考虑了以下两个方面:
1.在构建label时,为了处理遮挡问题,论文对被车辆遮挡的车道线和虚线进行了还原;
2. Loss使用交叉熵,为了解决样本分布不均衡的问题(属于车道线的像素远少于属于背景的像素),参考论文ENet: A Deep Neural Network Architecture for Real-Time Semantic Segmentation ,使用了boundedinverse class weight对loss进行加权:
$W_{class} = \frac{1}{ln(c+p_(class))}$
其中,p 为对应类别在总体样本中出现的概率,c 是超参数(ENet论文中是1.02,使得权重的取值区间为[1,50])。
实例分割
为了区分车道线上的像素属于哪条车道,embedding_branch 为每个像素初始化一个 embedding 向量,并且在设计 loss 时,使属同一条车道线的像素向量距离很小,属不同车道线的像素向量距离很大。
这部分的loss函数是由两部分组成:方差loss($L_{var}$)和距离loss($L_{dist}$):
$L_{var} = \frac{1}{C} \sum_{c=1}^{C} \frac{1}{N_c} [\Arrowvert \mu_c-x_i \Arrowvert -\delta_v]_{+}^{2}$
$L_{dist} = \frac{1}{C(C-1)} \sum_{c_A=1}^{C} \sum_{c_B=1, c_A \ne C_B}^{C} [\delta_d - \Arrowvert \mu_{c_A} - \mu_{c_B} \Arrowvert ]_{+}^{2}$
其中,C 是车道线数量,$N_c$ 是属同一条车道线的像素点数量,$\mu_c$ 是车道线的均值向量,$x_i$ 是像素向量(pixel embedding),$[x]_+ = max(0, x)$。
该 loss 函数源自于论文 《Semantic Instance Segmentation with a Discriminative loss function》 ,该论文中还有一个正则项,本文没有用:
$L_{reg} = \frac{1}{C} \sum_{c=1}^{C} \Arrowvert \mu_c \Arrowvert $
同一车道线的像素向量,距离车道线均值向量 $\mu_c$ 超过 $\delta_v$ 时, pull force($L_{var}$) 才有意义,使得 $x_i$ 靠近 $\delta_d$;
不同车道线的均值向量 $\mu_{c_A}$ 和 $\mu_{c_B}$ 之间距离小于 $\delta_d$ 时,push force($L_{dist}$) 才有意义,使得 $\mu_{c_A}$ 和 $\mu_{c_B}$ 彼此远离。
聚类
注意,聚类可以看做是个后处理,上一步里 embedding_branch 已经为聚类提供好的特征向量了,利用这些特征向量我们可以利用任意聚类算法来完成实例分割的目标。
为了方便聚类,论文中设定 $\delta_d > 6\delta_v$。
在进行聚类时,首先使用 mean shift 聚类,使得簇中心沿着密度上升的方向移动,防止将离群点选入相同的簇中;之后对像素向量进行划分:以簇中心为圆心,以 $2\delta_v$ 为半径,选取圆中所有的像素归为同一车道线。重复该步骤,直到将所有的车道线像素分配给对应的车道。
网络结构
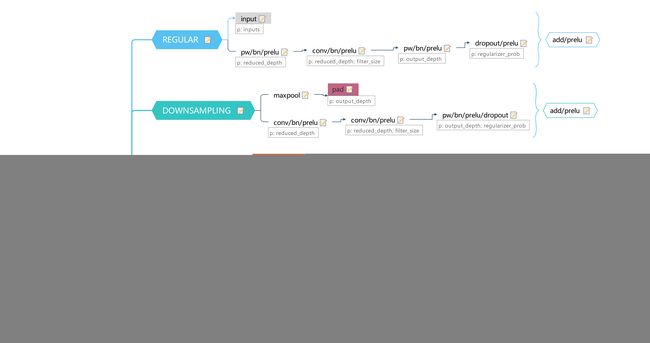
LaneNet是基于ENet 的encoder-decoder模型,如图5所示,ENet由5个stage组成,其中stage2和stage3基本相同,stage1,2,3属于encoder,stage4,5属于decoder。
如上图所示,在LaneNet 中,语义分割和实例分割两个任务共享 stage1 和 stage2,并将 stage3 和后面的 decoder 层作为各自的分支(branch)进行训练;其中,语义分割分支(branch)的输出 shape 为W*H*2,实例分割分支(branch)的输出 shape 为W*H*N,W,H分别为原图宽和高,N 为 embedding vector 的维度;两个分支的loss权重相同。
H-Net
LaneNet的输出是每条车道线的像素集合,还需要根据这些像素点回归出一条车道线。传统的做法是将图片投影到 bird’s-eye view 中,然后使用 2 阶或者 3 阶多项式进行拟合。在这种方法中,变换矩阵 H 只被计算一次,所有的图片使用的是相同的变换矩阵,这会导致地平面(山地,丘陵)变化下的误差。
为了解决这个问题,论文训练了一个可以预测变换矩阵 H 的神经网络 H-Net,网络的输入是图片,输出是变换矩阵 H:
通过置 0 对转置矩阵进行约束,即水平线在变换下保持水平。(即坐标 y 的变换不受坐标 x 的影响)
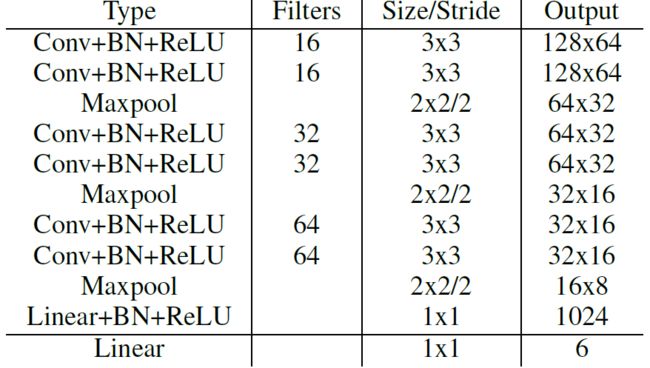
由上式可以看出,转置矩阵 H 只有6个参数,因此H-Net的输出是一个 6 维的向量。H-Net 由 6 层普通卷积网络和一层全连接网络构成,其网络结构如图所示:
Curve Fitting
Curve fitting的过程就是通过坐标 y 去重新预测坐标 x 的过程:
- 对于包含 N 个像素点的车道线,每个像素点 $p_i = [x_i, y_i, 1]^T \in P$, 首先使用 H-Net 的预测输出 H 对其进行坐标变换:
$P^{'} = HP$
- 随后使用 最小二乘法对 3d 多项式的参数进行拟合:
$w = (Y^TY)^{-1}Y^Tx^{'}$
- 根据拟合出的参数 $w = [\alpha, \beta, \gamma]^T$ 预测出 $x_i^{'*}$
$x_i^{'*} = \alpha y^{'2} + \beta y^{'} + \gamma$
- 最后将 $x_i^{'*}$ 投影回去:
$p_i^{*} = H^{-1}p_i^{'*}$
Loss function
$Loss = \frac{1}{N} \sum_{i=1}^{N}(x_i^{*} - x_i)^2 $
实验参数
LanNet
Dataset : Tusimple
Embedding dimension = 4
δ_v=0.5
δ_d=3
Image size = 512*256
Adam optimizer
Learning rate = 5e-4
Batch size = 8
H-Net
Dataset : Tusimple
3rd-orderpolynomial
Image size =128*64
Adam optimizer
Learning rate = 5e-5
Batch size = 10
评价标准
语义分割部分
$accuracy = \frac{2}{\frac{1}{recall} + \frac{1}{precision}}$
$recall = \frac{TP_1}{G_1}$
$precision = \frac{TP_0}{G_0}$
其中 $G_1$ 代表 GT二值图里像素值为 1 部分的数量,$TP_1$ 则代表预测结果里相对于 $G_1$, 预测正确的数量。
简单示例:
import numpy as np import tensorflow as tf out_logits = np.array([ [[0.1, 0.1, 0.1, 0.1, 0.1], [0.1, 0.2, 0.2, 0.8, 0.1], [0.1, 0.2, 0.2, 0.2, 0.1], [0.1, 0.2, 0.2, 0.2, 0.1], [0.1, 0.1, 0.1, 0.1, 0.1]], [[0.1, 0.1, 0.1, 0.1, 0.1], [0.1, 0.8, 0.8, 0.2, 0.1], [0.1, 0.8, 0.8, 0.8, 0.1], [0.1, 0.8, 0.8, 0.8, 0.1], [0.1, 0.1, 0.1, 0.1, 0.1]] ]) # 预测结果 binary_label = np.array([ [0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 0] ]) # GT logits = np.transpose(out_logits, (1, 2, 0)) out_logits = tf.constant(logits, dtype=tf.float32) binary_label_tensor = tf.constant(binary_label, dtype=tf.int32) binary_label_tensor = tf.expand_dims(binary_label_tensor, axis=-1) # =================== pix_cls_ret: 对于 GT 中为 1 的部分,统计 Pre 中是否分对,1对0错 out_logits = tf.nn.softmax(logits=out_logits) out = tf.argmax(out_logits, axis=-1) # 最后那个维度上的 max_idx out = tf.expand_dims(out, axis=-1) # 增加一维 5x5 -> 5x5x1 idx = tf.where(tf.equal(binary_label_tensor, 1)) pix_cls_ret = tf.gather_nd(out, idx) # =================== recall: 以GT 中像素值为 1 为基数,统计 recall = TP_1 / G1 recall = tf.count_nonzero(pix_cls_ret) # TP_1 recall = tf.divide(recall, tf.cast(tf.shape(pix_cls_ret)[0], tf.int64)) # =================== pix_cls_ret: 对于 GT 中为 0 的部分,统计 Pre 中是否分对,0对1错 idx = tf.where(tf.equal(binary_label_tensor, 0)) pix_cls_ret = tf.gather_nd(out, idx) # =================== precision: 以 GT 中像素值为 0 为基数,统计 precision = TP_0 / G0 precision = tf.subtract(tf.cast(tf.shape(pix_cls_ret)[0], tf.int64), tf.count_nonzero(pix_cls_ret)) # TP_0 precision = tf.divide(precision, tf.cast(tf.shape(pix_cls_ret)[0], tf.int64)) accuracy = tf.divide(2.0, tf.divide(1.0, recall) + tf.divide(1.0, precision)) with tf.Session() as sess: out_logits = out_logits.eval() out = out.eval() idx = idx.eval() pix_cls_ret = pix_cls_ret.eval() recall = recall.eval() precision = precision.eval() print(accuracy)
相关文献
LaneNet: Towards End-to-End Lane Detection: an Instance Segmentation Approach
ENet: A Deep Neural Network Architecture for Real-Time Semantic Segmentation
Discriminative Loss: Semantic Instance Segmentation with a Discriminative loss function